【数据结构】7.平衡搜索树（AVL树和红黑树）

0. 概述

　　对于普通的搜索树，如果一直插入比第一个元素小的元素，它会退化成一个无限向左下角眼神的单链表，使得时间复杂度退化为O(n)。如果我们在插入时保持树的结构是平衡的，则可以保证查找、插入和删除的时间复杂度有对数级的时间性能，下面讲到的AVL树和红黑树都是平衡搜索树，通过旋转来保持平衡

1. AVL树

1.1 定义

　　Adelson-Velskii 和 Landis 在 1962年提出的一种平衡树，保证搜索树的高度是O(logn)，这样就可以保证查找、插入和删除的时间为O(logn)

1.2 AVL树的描述

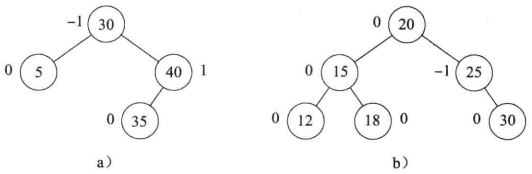
　　AVL 树一般用链表描述，为了简化插入和删除操作，为每个节点增加一个平衡因子 bf ，平衡因子 bf(x) 的定义为：x 的左子树的高度 - x 的右子树的高度

　　从 AVL 树的定义可以知道，平衡因子 bf 的取值为 -1、0 和 1

1.3 AVL树的搜索

　　与普通的搜索树相同，根据 theKey 不断向左孩子或右孩子移动寻找即可，时间复杂度为O(logn)

1.4 AVL树的插入

　　首先是区分4种旋转情况的代码，具体在1.4.1-1.4.4部分

template<class K, class V>
bool avlTree<K, V>::insert(K key, V val)
{
    // 1.根节点为空，直接插入
    if (_root == NULL)
    {
        _root = new Node<K, V>(key, val);
        return true;
    }
    // 2.根节点不为空
    else
    {
        Node<K, V>* cur = _root;
        Node<K, V>* parent = NULL;

        // 2.1)找到要插入节点的位置
        while (cur!=NULL)
        {
            parent = cur;
            if (cur->_key > key)
                cur = cur->_left;
            else if (cur->_key < key)
                cur = cur->_right;
            else
                return false;   //不允许出现重复元素的节点
        }

        // 2.2)插入新节点
        cur = new  Node<K, V>(key, val);
        if (parent->_key > key)
        {
            parent->_left = cur;
            cur->_parent = parent;
        }
        else
        {
            parent->_right = cur;
            cur->_parent = parent;
        }

        // 2.3)插入完成后，调整平衡因子
        while (parent!=NULL)
        {
            if (cur == parent->_left)//插入节点在左子树父节点bf++，反之--
                parent->_bf++;
            else
                parent->_bf--;

            // 2.3.1)插入新节点后，双亲结点高度为0, 说明这个父节点原先已有一个孩子, 这次插入到另一个孩子的位置了, 树整体的高度无变化, 结束
            if (parent->_bf == 0)
                break;
            // 2.3.2)插入节点后双亲节点高度为-1或1, 说明子树高度改变，则继续向上调整
            else if (parent->_bf == -1 || parent->_bf == 1)
            {
                cur = parent;
                parent = parent->_parent;
            }
            // 2.3.3)插入节点后parent->_bf==-2||parent->_bf==2；说明已经不平衡，需要旋转
            else
            {
                if (parent->_bf == 2)
                {
                    if (cur->_bf == 1)
                        rotateLL(parent);    // parent(2), child(1)
                    else
                        rotateLR(parent);    // parent(2), child(-1)

                }
                else
                {
                    if (cur->_bf == -1)
                        rotateRR(parent);    // parent(-2), child(-1)
                    else
                        rotateRL(parent);    // parent(-2), child(1)
                }
                break;
            }
        }
        return true;
    }
}

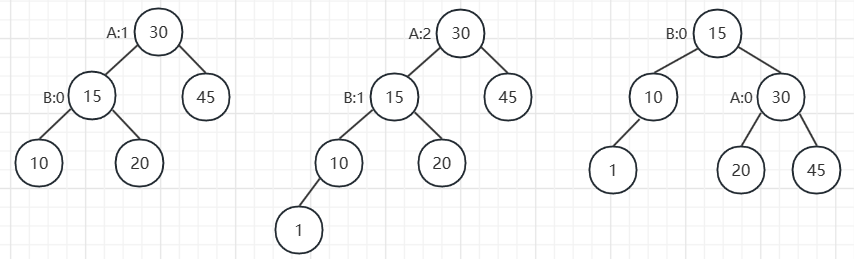
1.4.1 LL型不平衡（单旋转）

　　插入前左子树高度比右子树高度高 1，然后在左子树的左侧插入一个新的元素，只需要一次 右单旋 就可以转为平衡搜索树。具体操作如下，根节点A的左孩子B转换为新的根节点，B的右孩子转换为A的左孩子

template <class K, class V>
void avlTree<K, V>::rotateLL(Node<K, V>* parent)
{
    Node<K, V>* subL = parent->_left;
    Node<K, V>* subLR = subL->_right;
    Node<K, V>* ppNode = parent->_parent;

    // 一共两步, 重新连接节点即可
    parent->_left = subLR;      // 1.当前 parent 节点的左孩子 改成 其左孩子的右孩子
    if (subLR != NULL)
        subLR->_parent = parent;

    subL->_right = parent;      // 2.把当前 parent 节点改成 subL 的右孩子
    parent->_parent = subL;

    if (_root == parent)        // 判断不平衡的点是不是根节点
    {
        _root = subL;
        subL->_parent = NULL;
    }
    else
    {
        if (ppNode->_right == parent)
        {
            ppNode->_right = subL;
        }
        else
        {
            ppNode->_left = subL;
        }

        subL->_parent = ppNode;
    }

    subL->_bf = 0;
    parent->_bf = 0;
}

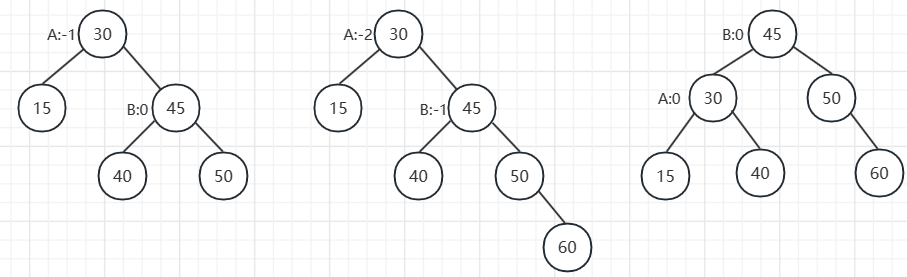
1.4.2 RR型不平衡（单旋转）

　　插入前右子树高度比左子树高度高 1，然后在右子树的右侧插入一个新的元素，只需要一次 左单旋 就可以转为平衡搜索树。具体操作如下，根节点A的右孩子B转换为新的根节点，B的左孩子转换为A的右孩子

template <class K, class V>
void avlTree<K, V>::rotateRR(Node<K, V>* parent)
{
    Node<K, V>* subR = parent->_right;
    Node<K, V>* subRL = subR->_left;
    Node<K, V>* pParent = parent->_parent;

    // 一共两步, 重新连接节点即可
    parent->_right = subRL;      // 1.当前 parent 节点的右孩子 改成 其右孩子的左孩子
    if (subRL != NULL)
        subRL->_parent = parent;

    subR->_left = parent;       // 2.把当前 parent 节点改成 subR 的左孩子
    parent->_parent = subR;

    if (parent == _root)        // 判断不平衡的点是不是根节点
    {
        _root = subR;
        _root->_parent = NULL;
    }

    else
    {
        if (pParent->_left = parent)
            pParent->_left = subR;
        else
            pParent->_right = subR;

        subR->_parent = pParent;
    }
    parent->_bf = 0;
    subR->_bf = 0;
}

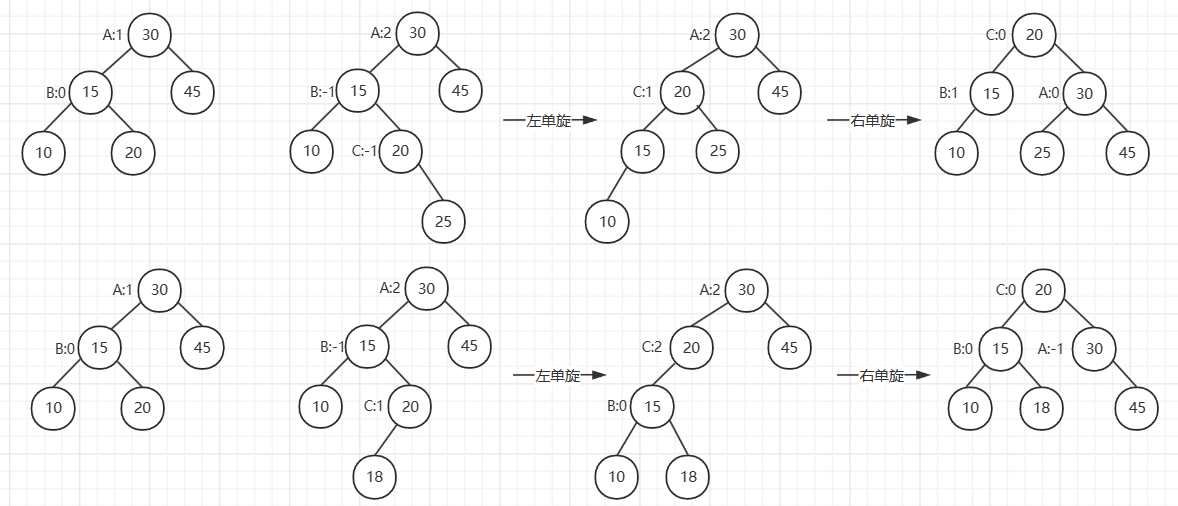
1.4.3 LR型不平衡（双旋转）

　　左子树高度更高的情况下，在左子树的右侧插入一个节点。首先进行一次 左单旋 ，将它转换为LL型不平衡，然后进行一次 右单旋 转换为平衡搜索树

template <class K, class V>
void avlTree<K, V>::rotateLR(Node<K, V>* parent)
{
    Node<K, V>* subL = parent->_left;
    Node<K, V>* subLR = subL->_right;
    int bf = subLR->_bf;

    rotateRR(parent->_left);
    rotateLL(parent);

    if (bf == 1)
    {
        parent->_bf = 0;
        subL->_bf = -1;
        subLR->_bf = 0;
    }
    else if (bf == -1)
    {
        parent->_bf = 1;
        subL->_bf = 0;
        subLR->_bf = 0;
    }
}

1.4.4 RL型不平衡（双旋转）

　　与LR型不平衡类似，这里直接给出代码

template <class K, class V>
void avlTree<K, V>::rotateRL(Node<K, V>* parent)
{
    Node<K, V>* subR = parent->_right;
    Node<K, V>* subRL = subR->_left;
    int bf = subRL->_bf;

    rotateLL(parent->_right);
    rotateRR(parent);

    if (bf == 1)
    {
        subR->_bf = 0;
        parent->_bf = -1;
        subRL->_bf = 0;
    }
    else if (bf == -1)
    {
        parent->_bf = 0;
        subR->_bf = 1;
        subRL->_bf = 0;
    }
}

2. 红黑树（red-black tree）

2.1 基本概念

　　红黑树是一棵扩充二叉树，每个空指针用一个外部节点来代替，除此之外还有以下性质

• 根节点和外部节点颜色都是黑色
• 在根节点到外部节点的路径上，没有连续两个节点是红色
• 在所有根节点到外部节点的路径上，黑色节点的数目都相同

　　红黑树一个节点的阶（rank）：从该节点到一外部节点的路径上黑色节点的数量

　　红黑树最大的高度是2log₂(n+1)

2.2 RBT的搜索

　　与普通的搜索树相同，根据 theKey 不断向左孩子或右孩子移动寻找即可，时间复杂度为O(logn)

2.3 RBT的插入

　　我们的插入目标实际上是，和普通搜索树一样插入一个元素，然后再让它额外满足红黑树的性质。

2.3.1 情况一：变色处理

　　这种情况是最简单的情况，如果插入节点的叔叔节点（父亲的对称孩子）也是红色，则只需要进行变色处理

• 父亲节点和叔叔节点变为黑色
• 曾祖父节点变为红色

　　循环处理直到根节点为止，最后将根节点变为黑色结束

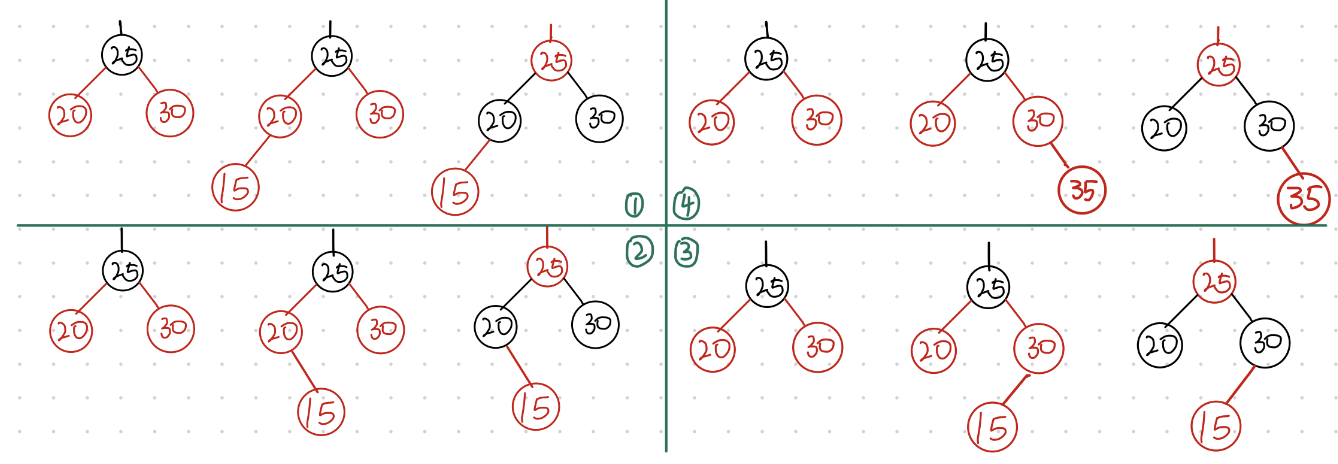
2.3.2 情况二：单旋加变色处理

　　如果新插入节点的叔叔为黑色，并且新插入节点在外侧

• 进行一次单旋转
• 把父亲节点更改为黑色，曾祖父节点更改为红色（最后这个三角形是黑色连两个红色）

2.3.3 情况三：双旋加变色处理

　　如果新插入节点的叔叔为黑色，并且新插入节点在内测

• 对父亲节点进行一次单旋转
• 对曾祖父节点进行一次单旋转
• 将新插入节点修改为黑色，曾祖父节点修改为红色（最后这个三角形是黑色连两个红色）

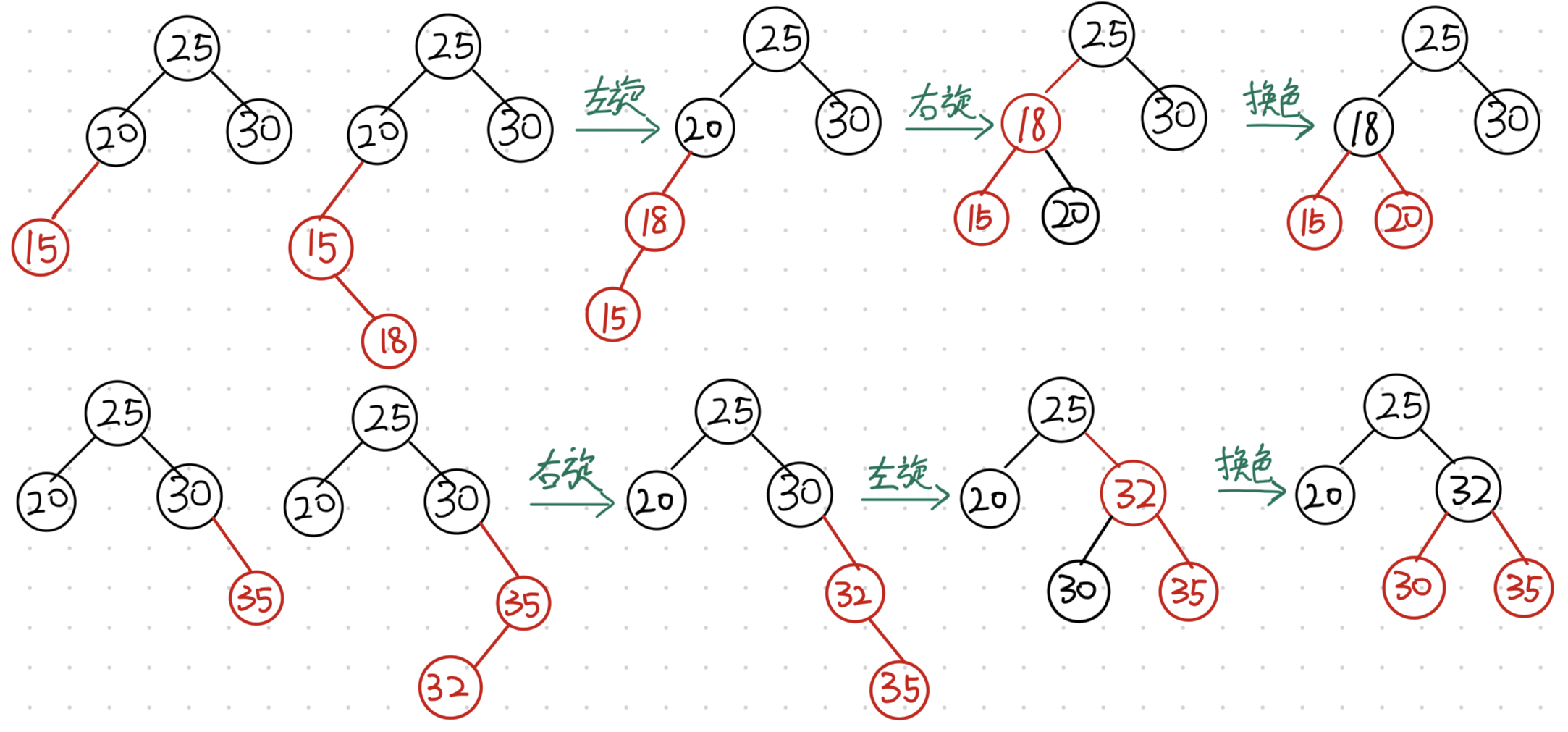
2.3.4 RBT插入的实现

2.3.4.1 对外暴露的插入函数

template <class K, class V>
bool RBTree<K, V>::insert(K key, V val)
{
    RBTNode<K, V>* z = NULL;

    if ((z = new RBTNode<K, V>(key, val, RED, NULL, NULL, NULL)) == NULL)
        return false;

    return insert(this->_root, z);
}

2.3.4.2 按照普通的搜索树进行插入操作

template <class K, class V>
bool RBTree<K, V>::insert(RBTNode<K, V>*& root, RBTNode<K, V>* node)
{
    // 1.根节点为空，直接插入
    if (root == NULL)
    {
        node->_color = BLACK;
        root = node;
        return true;
    }
    // 2.根节点不为空
    else
    {
        RBTNode<K, V>* cur = root;
        RBTNode<K, V>* parent = NULL;

        // 2.1)找到要插入节点的位置
        while (cur != NULL)
        {
            parent = cur;
            if (node->_key < cur->_key)
                cur = cur->_left;
            else if (node->_key > cur->_key)
                cur = cur->_right;
            else
                return false;   //不允许出现重复元素的节点
        }

        // 2.2)插入新节点
        if (parent->_key > node->_key)
        {
            parent->_left = node;
            node->_parent = parent;
        }
        else
        {
            parent->_right = node;
            node->_parent = parent;
        }

        return insertFixUp(root, node);
    }
}

2.3.4.3 插入完成后的颜色修正

template <class K, class V>
bool RBTree<K, V>::insertFixUp(RBTNode<K, V>*& root, RBTNode<K, V>* node)
{
    RBTNode<K, V>* parent, * grandparent, * cur;
    cur = node;
    parent = cur->_parent;

    // 若“父节点存在，并且父节点的颜色是红色”
    while (parent && rb_is_red(parent))
    {
        grandparent = parent->_parent;

        //若“父节点”是“祖父节点的左孩子”
        if (parent == grandparent->_left)
        {
            RBTNode<K, V>* uncle = grandparent->_right;

            if (uncle && rb_is_red(uncle))
            {// 情况1：叔叔节点是红色, 修改后继续检查
                rb_set_black(uncle);
                rb_set_black(parent);
                rb_set_red(grandparent);
                cur = grandparent;
                parent = cur->_parent;
            }
            else
            {// 情况2: 叔叔节点不存在或者是黑色, 修改后结束循环
                if (parent->_left == cur)
                {// 情况2.1：叔叔是黑色，且当前节点是左孩子 (单旋+变色)
                    rightRotate(grandparent);
                    rb_set_black(parent);
                    rb_set_red(grandparent);
                }
                else
                {// 情况2.2：叔叔是黑色，且当前节点是右孩子
                    leftRotate(parent);
                    rightRotate(grandparent);
                    rb_set_black(cur);
                    rb_set_red(grandparent);
                }
                break;
            }
        }
        else//若“父节点”是“祖父节点的右孩子”
        {
            RBTNode<K, V>* uncle = grandparent->_left;

            if (uncle && rb_is_red(uncle))
            {
                rb_set_black(uncle);
                rb_set_black(parent);
                rb_set_red(grandparent);
                cur = grandparent;
                parent = cur->_parent;
            }
            else
            {
                if (parent->_right == cur)
                {
                    leftRotate(grandparent);
                    rb_set_black(parent);
                    rb_set_red(grandparent);
                }
                else
                {
                    rightRotate(parent);
                    leftRotate(grandparent);
                    rb_set_black(cur);
                    rb_set_red(grandparent);
                }
            }
        }
    }
    // 将根节点设为黑色
    rb_set_black(root);
    return true;
}