hdu3068-最长回文-马拉车(Manacher)算法

http://acm.hdu.edu.cn/showproblem.php?pid=3068

脑子转个弯总算看懂马拉车算法了。记录一下思路和模板。

马拉车算法是在O(n)的时间内求出最大回文子串。

一、变量和定义

为了对奇偶回文串统一处理，每个字符之间都加上一个字符，加上一个不会出现在原字符串的，

如"abba"变成"#a#b#b#a#";"aba"变成"#a#b#a#";无论是奇偶原串都变成了奇数新串，接下来对新串处理。

在一次遍历字符的过程中，变量名及意义

i:表示当前遍历到哪一个下标的字符

p[idx]:表示下标为idx的字符的回文半径，包括自身

id:目前遍历过程中能延展到最右的回文的中心点

mx:目前遍历过程中能延展到最右的下标位置，姑且称之为探测的最远长度

j:以id为中心的关于i对称的字符，在id的左边，已经遍历过了，p[j]已经确定了的

---

二、为何要记录每个遍历字符的回文半径呢？利用已有的信息为后面的遍历铺垫，否则就和中心扩展一样是O(n²)复杂度

1."abcecbd"加上'#'后变成"#a#b#c#e#c#b#d#"

下标 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

内容 # a # b # c # e # c #  b  #  d  #

p[i] 1 2 1 2 1 2 1 6 1 2 1  2  1  2  1

最长回文子串"#b#c#e#c#b#"的中心字符为e，下标为7，减去p[7]之后等于1，表示最长回文子串"bcecb"在原串"abcecbd"中的下标为1(从0算起)

2."abbc"加上'#'后变成"#a#b#b#c#"

下标 0 1 2 3 4 5 6 7 8

内容 # a # b # b # c #

p[i] 1 2 1 2 3 2 1 2 1

最长回文子串"#b#b#"的中心字符为#，下标为4，减去p[4]=3之后等于1,表示最长回文子串"bb"在原串"abbc"中的下标为1(从0算起)

3."aba"加上'#'后变成"#a#b#a#"

下标 0 1 2 3 4 5 6

内容 # a # b # a #

p[i] 1 2 1 4 1 2 1

最长回文子串"#a#b#a#"的中心字符为b，下标为3，减去p[3]=4之后等于-1,与前面不一致。原串最长回文子串应该是下标从0开始，则需要向右移动1位

4.在最左边加一个字符'$'(不会在原串中出现)，则变成"$#a#b#a#"

下标 0 1 2 3 4 5 6 7

内容 $ # a # b # a #

p[i] 1 1 2 1 4 1 2 1

则最长回文子串"#a#b#a#"的中心字符为b，下标为4，减去p[3]=4之后等于0,与"aba"在"aba"的起始位置一致。

再回顾前2个例子

5."#a#b#c#e#c#b#d#"在首位加上'$'

下标 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

内容 $ # a # b # c # e # c  #  b  #  d  #

p[i] 1 1 2 1 2 1 2 1 6 1 2  1  2  1  2  1

最长回文子串"#b#c#e#c#b#"的中心字符为e，下标为8，减去p[8]=6之后等于2，但是最长回文子串"bcecb"在原串"abcecbd"中的下标为1，除以2可以得到，对于上一个例子0没有影响，再通过另一个例子验证。

6."#a#b#a#"在首位加上'$'

下标 0 1 2 3 4 5 6 7 8 9

内容 $ # a # b # b # c #

p[i] 1 1 2 1 2 3 2 1 2 1

最长回文子串"#b#b#"的中心字符为#，下标为5，减去p[5]=3之后等于2,但是最长回文子串"bb"在原串"abbc"中的下标为1，除以2可以得到

7.经过多方尝试都能通过验证。

首位加上一个不相干的字符后，原串的最长回文子串起始位置=(新串的最长回文中心id-p[id])/2

---

三、算法过程

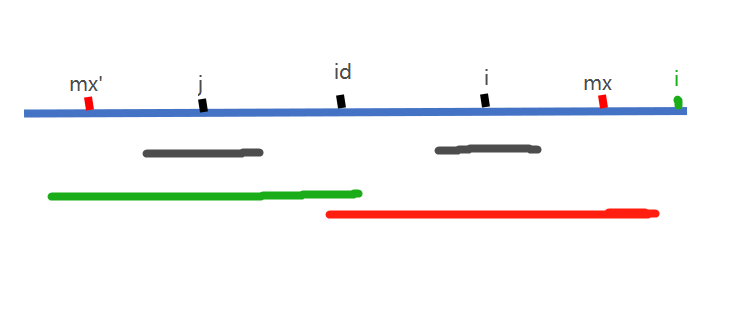
1.如果i在mx左边，则i在以id为中心的回文子串内部，则与j对称；以j为中心的回文，i必然也有，对于j的回文情况p[j],再分两种情况讨论

(1)i+p[j]使得i右边大于等于mx，即(i+p[j])>=mx,则p[i]取(mx-i)即可

(2)(i+p[j])<mx,则p[i]=p[j]

2.如果i再mx右边，则先设p[i]=1

3.暂定了p[i]，仍需要中心扩展。（马拉车的精髓就在这里，一次性可能定了一个巨大的p[i],而不是每次都从1慢慢中心扩展，节省时间）

4.防止中心扩展时候某一边会越界，尾部也加个乱七八糟的字符堵住,例如'!'

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<math.h>
#include<string>
#include<map>
#include<queue>
#include<stack>
#include<set>
#include<ctime>
#define ll long long
#define inf 0x3f3f3f3f
const double pi=3.1415926;
using namespace std;
int p[*+];

int Manacher(string s)
{
    int ans=;
    int id=,mx=;
    memset(p,,sizeof(p));
    int len=s.size();
    for(int i=;i<len;i++)
    {
        int j=*id-i;///对称点
        if(mx>i) ///i在已探测的范围内
        {
            if(mx-i>=p[j])
                p[i]=p[j];
            else
                p[i]=mx-i;
        }
        else
            p[i]=;

        ///暂定了p[i]，还是有可能更大，中心扩展
        while( s[ i+p[i] ] == s[ i-p[i] ] )///前后加入不相干字符，不会越界
            p[i]++;
        if(i+p[i]>mx)///更新最右点和对应的id
        {
            id=i;
            mx=id+p[id];
        }
        ans=max(ans,p[i]);
    }
    return ans-;
}

int main()
{
    ios::sync_with_stdio(false);//加速
    string str,s;
    while(cin>>str)
    {
        s="$#";
        int len=str.size();
        for(int i=;i<len;i++)
        {
            s += str[i];
            s += "#";
        }
        s=s+"!";
        cout<<Manacher(s)<<endl;
    }
    return ;
}

运用了马拉车算法，本题还有2个可能出现的坑

• 坑1：如果同c++的string输入字符串，需要加速
• 坑2：string的拼接：str =str+ "a"加的运算产生的是一个新的对象，再把结果返回，而str += "a" 涉及到的应该是对象的引用，操作之后直接返回引用，避免了产生新的对象。因此，两者的性能有一定的差距。+=的写法更快。

真的是被坑得神不知鬼不觉，T了十几发才找到错误