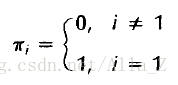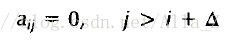隐马尔可夫模型(HMM)的分类
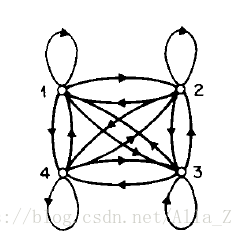
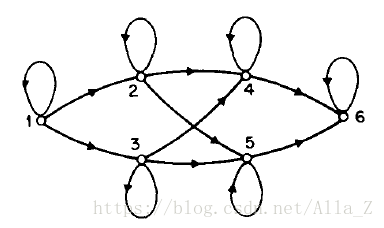
1、遍历型(ergodic model)
即每个状态都可以由任意一个状态演变而来,aij>0,for all i , j. 如图:
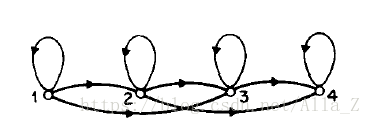
2、left-right type of HMM
每个状态只能由下标值小于当前值得状态以及其本身转移而来,即从左向右转移。因此状态转移矩阵有如下特性:

这种由左向右转移的HMM转移状态矩阵为上半矩阵,同时此类型矩阵一般同时存在一个最长跳跃距离,即有
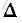
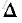
这种类型的HMM模型能够非常好的用于随时间变化的信号,比如语音信号。
3、其他类型
上图所示HMM模型严格来说也属于left-right type of HMM,但是它又存在它自己独特的规则,更类似于两个平行的left-right HMM的组合模型。
但是我们应该明白,对于不同类型的HMM,对于学习问题的求解来说步骤都是一样的。
隐马尔可夫模型(HMM)的分类的更多相关文章
- 基于隐马尔科夫模型(HMM)的地图匹配(Map-Matching)算法
文章目录 1. 1. 摘要 2. 2. Map-Matching(MM)问题 3. 3. 隐马尔科夫模型(HMM) 3.1. 3.1. HMM简述 3.2. 3.2. 基于HMM的Map-Matchi ...
- 隐马尔科夫模型HMM学习最佳范例
谷歌路过这个专门介绍HMM及其相关算法的主页:http://rrurl.cn/vAgKhh 里面图文并茂动感十足,写得通俗易懂,可以说是介绍HMM很好的范例了.一个名为52nlp的博主(google ...
- 猪猪的机器学习笔记(十七)隐马尔科夫模型HMM
隐马尔科夫模型HMM 作者:樱花猪 摘要: 本文为七月算法(julyedu.com)12月机器学习第十七次课在线笔记.隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来 ...
- 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型HMM(一)HMM模型
隐马尔科夫模型HMM(一)HMM模型基础 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比 ...
- 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态序列
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态 ...
- 用hmmlearn学习隐马尔科夫模型HMM
在之前的HMM系列中,我们对隐马尔科夫模型HMM的原理以及三个问题的求解方法做了总结.本文我们就从实践的角度用Python的hmmlearn库来学习HMM的使用.关于hmmlearn的更多资料在官方文 ...
- HMM:隐马尔可夫模型HMM
http://blog.csdn.net/pipisorry/article/details/50722178 隐马尔可夫模型 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模 ...
- 机器学习之隐马尔科夫模型HMM(六)
摘要 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔科夫过程.其难点是从可观察的参数中确定该过程的隐含参数,然后利用这些参数来作进一步 ...
随机推荐
- 「ZJOI2019」麻将
传送门 Solution 对于条件一:记录一个\(cnt\)表示牌个数\(≥2\)的个数 设\(dp_{i,0/1,j,k}\)表示考虑了\(1...i\),当前是否有对子,以\(i-1\),\(i ...
- np.concatenate
- svg复用方式<g>, <defs>, <symbol>, <use>
svg复用元素的方式主要有 <g>, <defs>, <symbol>, <use> 1. <g> group, 分组,定义一组元素,初始不 ...
- Appium脚本(2):元素检测
场景: 有的按钮在第一次打开时显示,之后就不显示了,如更新提示.特性介绍等,面对这样的场景写了如下脚本,增加脚本的复用性. no_element_exception_2.py from appium ...
- vue+element-ui+ajax实现一个表格的实例
<!DOCTYPE html> <html> <head> <script src="js/jquery-3.2.1.js">< ...
- 【python基础】argparse模块
参考 1. argumentparser-objects: 2. argparse.ArgumentParser()用法解析:
- flex布局大全 2019
有句话叫做:存在即是合理. 最近很喜欢flex布局模式,不过还在摸索中,这里正一边在项目中使用和总结,也在学习一些大牛们总结的东西和布局思考. 鉴于自己很苦恼,到处去ha资料,真的,就没有一个系统的, ...
- [LeetCode] 682. Baseball Game 棒球游戏
You're now a baseball game point recorder. Given a list of strings, each string can be one of the 4 ...
- 【SSH进阶之路】Spring的AOP逐层深入——AOP的基本原理(六)
经过我们对Spring的IOC不断的深入学习,Spring的面貌逐渐变得清晰,我们对Spring的了解也更加的深入.从这篇博文开始我们学习Spring的第二大核心内容:AOP. 什么是AOP AOP( ...
- 【视频开发】【Live555】摄像头采集,264编码,live555直播(0)
参看 有关live555 1.首先需要修改live555,定义从 内存中直接获取source而不是从文件读取source的类. 自己实现的类命名为 H264FramedLiveSource /* ...