算法入门经典-第七章 例题7-4-1 拓展 n皇后问题 回溯法

实际上回溯法有暴力破解的意思在里面，解决一个问题，一路走到底，路无法通，返回寻找另   一条路。

回溯法可以解决很多的问题，如：N皇后问题和迷宫问题。

一.概念

回溯算法实际类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现不满足条件的时候，就回溯返回，尝试别的路径。

百度解释：回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

二.基本思想

在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。（其实回溯法就是对隐式图的深度优先搜索算法）。

若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。

而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。

三.n皇后问题

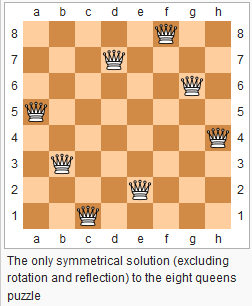
////N皇后是典型DPS问题，这里是用递归实现的，要想输出必须要存储上级运算结果。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<string>
#include<cctype>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<stack>
#include<ctime>
#include<algorithm>
#include<climits>
using namespace std;
const int N=;
   static int disp[];
int C[N];
int tot;
int n;
void search(int cur)
{

    if(cur==n){
            for( int i = ; i<n; i++ )
   printf( "%d " , disp[i] );
   printf("\n");
   tot++;
   }
    else
     for(int i=;i<n;i++)
    {
        int ok=;
        C[cur]=i;//尝试把cur行的皇后放在第i列
        for(int j=;j<cur;j++)//检查是否和前面的皇后冲突
        if(C[cur]==C[j]||cur-C[cur]==j-C[j]||cur+C[cur]==j+C[j])
        {
            ok=;break;
        }

    if(ok) {
          disp[cur]=i;//当前行的皇后在第几列
                search(cur+);
                }
}
}
int main()
{
    while(cin>>n)
    {
        tot=;
        search();
        cout<<tot<<"种方法"<<endl;
    }
    return ;
}   

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
using namespace std;
int c[],vis[][],tot,n=,sum_max;
int mapn[][];
void search(int cur)
{
    if(cur==n)//递归边界，只要走到了这里，所有皇后必然不冲突
    {
        if(sum_max<tot)
            sum_max = tot;
    }
    else for(int i=;i<n;i++)
    {
        if(!vis[][i]&&!vis[][cur+i]&&!vis[][cur-i+n])//利用二维数组直接判断
        {//0为竖行，1为副对角线，2为主对角线
            c[cur] = i;//保存下每行皇后的位置
            tot += mapn[cur][i];
            vis[][i] = vis[][cur+i] = vis[][cur-i+n] = ;
            search(cur+);
            vis[][i] = vis[][cur+i] = vis[][cur-i+n] = ;//记得改回来
            tot -= mapn[cur][i];
        }
    }
}
int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        sum_max = ,tot = ;
        memset(vis,,sizeof(vis));
        for(int i=;i<;i++)
            for(int j=;j<;j++)
            {
                cin >> mapn[i][j];
            }
        search();
        printf("%5d\n",sum_max);
    }
    return ;
}