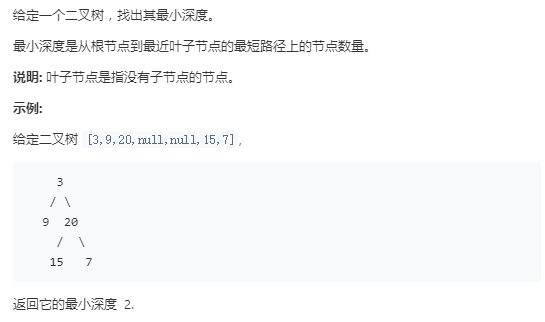
树、递归、广度优先搜索（BFS）————二叉树的最小深度

解法一：递归 遇到叶子节点不递归，否则接着往子树递归，每次递归层数加1

要确定的是，一定要保证初始输入的节点是有子节点的。因为可能出现只有单子树的情况，所以要先确认这种情况。

具体过程：

1、分析初始条件

空指针：深度为0

单节点：深度为1

1、先确定递归基本条件：

节点指针为空，说明深度为0，返回深度0；

如果到了叶节点，说明其左右两节点指针就是空，也就是在深度为0的基础上加上该节点所在的一层，即1+调用空指针的递归函数

2、找最近的叶节点，也就是左右指针都是空的叶节点的时候。

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  * };
  */
 class Solution {
 public:
     int minDepth(TreeNode* root) {
         if(root==NULL) return ;//root节点是空节点，深度为0
                  if(!root->right && !root->left) return ;//只有一个节点，深度就是1
         if(!root->left){//左节点空，右节点非空，在右子树里面找最近的叶子节点
             return +minDepth(root->right);
         }
         if(!root->right){//右节点空，左节点非空，在左子树里面找最近的叶子节点
             return +minDepth(root->left);
         }
         //两个节点都非空，那就继续迭代下一层
         return +min(minDepth(root->left),minDepth(root->right));
     }
 };

方法二：

BFS，广度优先搜索 每次把一层节点压入队列，同时判断这些节点中是否含有叶子节点（即左右指针都为空），若有，说明找到了最近的那个叶子节点，返回层数。

 class Solution {
 public:
     int minDepth(TreeNode* root) {
         if(root==NULL) return ;  //判空
         queue<pair<TreeNode*,int>> que;  //把节点和所在的层数绑定
         que.push(make_pair(root,)); //压入根节点，层数为1
         while()
         {
             TreeNode* node=que.front().first; //当前节点
             int level=que.front().second;  //层数
             que.pop();
             if (!node->left && !node->right) return level;//遇到叶子节点
             if(node->left) //压入左节点
                 que.push(make_pair(node->left,level+));
             if(node->right)//压入右节点
                 que.push(make_pair(node->right,level+));
         }
     }
 };