hdu----(5047)Sawtooth(大数相乘+数学推导)

Sawtooth

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 422    Accepted Submission(s): 134

Problem Description

Think about a plane:

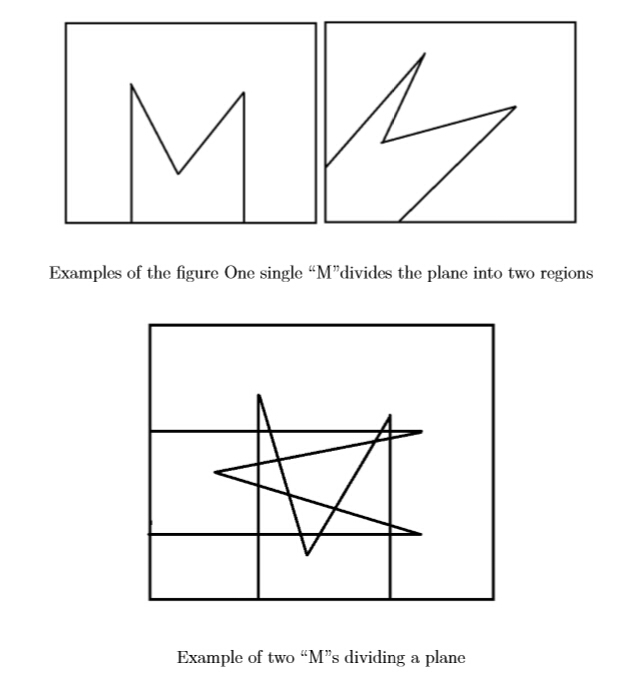
● One straight line can divide a plane into two regions.
● Two lines can divide a plane into at most four regions.
● Three lines can divide a plane into at most seven regions.
● And so on...

Now we have some figure constructed with two parallel rays in the
same direction, joined by two straight segments. It looks like a
character “M”. You are given N such “M”s. What is the maximum number of
regions that these “M”s can divide a plane ?

 

Input

The first line of the input is T (1 ≤ T ≤ 100000), which stands for the number of test cases you need to solve.

Each case contains one single non-negative integer, indicating number of “M”s. (0 ≤ N ≤ 10¹²)

 

Output

For each test case, print a line “Case #t: ”(without quotes, t means
the index of the test case) at the beginning. Then an integer that is
the maximum number of regions N the “M” figures can divide.

 

Sample Input

2
1
2

 

Sample Output

Case #1: 2
Case #2: 19

 

Source

2014 ACM/ICPC Asia Regional Shanghai Online

 

 

其实题目已经很清楚的告知我们是有线条分平面引申而来的了....

对于线条分平面

0  1

1  1 +1

2  1+1 +2

3 1+1 +2+3

4 1+1 +2+3+4

............

n   1+n(n+1)/2;

那么对于一个m型号的模型，其实我们可以将其视其为四条线段组合而成，这样这个公式就变为：

 4n*(4n+1)/2 +1  ---->显然得到的答案有余坠，我

0  1

1   11    2       9

2   37    19     9*2

......

推到得到：

 4n*(4n+1)/2  +1 -8*n----> 8n^2-7n+1

代码：

 #include<cstdio>
 #include<cstring>
 char aa[],bb[];
 int ans[];
 int mul( char *a, char *b, int temp[])
 {

     int i,j,la,lb,l;
     la=strlen(a);
     lb=strlen(b);

     for ( i=;i<la+lb;i++ )
         temp[i]=;
     for ( i=;i<=la-;i++ ) {
           l=i;
         for ( j=;j<=lb-;j++ ) {
             temp[l]=(b[j]-'')*(a[i]-'')+temp[l];
             l++;
         }
     }
     while ( temp[l]== )
         l--;
     for ( i=;i<=l;i++ ) {
         temp[i+]+=temp[i]/;
         temp[i]=temp[i]%;
     }
     if ( temp[l+]!= )
         l++;

     while ( temp[l]/!= ) {
         temp[l+]+=temp[l]/;
         temp[l]=temp[l]%;
         l++;
     }
     if ( temp[l]== )
         l--;
     return l;
 }
 void cal(__int64 a,char *str)
 {
     int i=;
     while(a>)
     {
      str[i++]=(a%)+'';
      a/=;
     }
 }
 int main()
 {
     int cas;
     __int64 n;
     scanf("%d",&cas);
     for(int i=;i<=cas;i++)
     {
       scanf("%I64d",&n);
       printf("Case #%d: ",i);
       if(n==)printf("1\n");
       else
       {
       memset(aa,'\0',sizeof(aa));
       memset(bb,'\0',sizeof(bb));
       memset(ans,,sizeof(ans));
       //,(8*n-7)*n+1
       cal(*n-,aa);
       cal(n,bb);
       int len=mul(aa,bb,ans);
        ans[]++;
        int c=;
      for(int j=;j<=len;j++)
      {
          ans[j]+=c;
        if(ans[j]>)
         {
           c=ans[j]/;
           ans[j]%=;
         }
      }
       if(c>)
         printf("%d",c);
       for(int j=len;j>=;j--)
         printf("%d",ans[j]);
     printf("\n");
     }
     }
  return ;
 }