Codeforces Round #232 (Div. 2) On Sum of Fractions

Let's assume that

• v(n) is the largest prime number, that does not exceed n;
• u(n) is the smallest prime number strictly greater than n.

Find .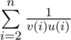

Input

The first line contains integer t (1 ≤ t ≤ 500) — the number of testscases.

Each of the following t lines of the input contains integer n (2 ≤ n ≤ 109).

Output

Print t lines: the i-th of them must contain the answer to the i-th test as an irreducible fraction "p/q", where p, q are integers, q > 0.

Sample test(s)

input

2
2
3

output

1/6
7/30

分析：把公式分解1/(p*q)=1/(p-q) *  (1/q-1/p) 然后求和发现公式：ans=(-2q+2*n-2*p+2+2*q*q)/(2*u*v);

 1 #include<cstdio>
 2 #include<cmath>
 3 #include<algorithm>
 4 using namespace std;
 5 bool isprime(unsigned long long x)
 6 {
 7     int idx=sqrt(x);
 8     for(int i=; i<=idx; ++i)
 9         if(x%i==)
             return false;
     return true;
 }
 int main()
 {
     int t;
     unsigned long long n;
     scanf("%d",&t);
     while(t--)
     {
         scanf("%I64u",&n);
         unsigned long long v=n,u=n+;
         while(!isprime(v))
             --v;
         while(!isprime(u))
             ++u;
         unsigned long long p=v*u-*u+*n-*v+,q=*v*u,tmp=__gcd(p,q);
         printf("%I64u/%I64u\n",p/tmp,q/tmp);
     }
 }