poj 3608 凸包间的最小距离

Bridge Across Islands

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 7632		Accepted: 2263		Special Judge

Description

Thousands of thousands years ago there was a small kingdom located in the middle of the Pacific Ocean. The territory of the kingdom consists two separated islands. Due to the impact of the ocean current, the shapes of both the islands became convex polygons. The king of the kingdom wanted to establish a bridge to connect the two islands. To minimize the cost, the king asked you, the bishop, to find the minimal distance between the boundaries of the two islands.

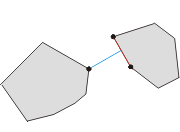
Input

The input consists of several test cases. Each test case begins with two integers N, M. (3 ≤ N, M ≤ 10000) Each of the next N lines contains a pair of coordinates, which describes the position of a vertex in one convex polygon. Each of the next M lines contains a pair of coordinates, which describes the position of a vertex in the other convex polygon. A line with N = M = 0 indicates the end of input. The coordinates are within the range [-10000, 10000].

Output

For each test case output the minimal distance. An error within 0.001 is acceptable.

Sample Input

4 4
0.00000 0.00000
0.00000 1.00000
1.00000 1.00000
1.00000 0.00000
2.00000 0.00000
2.00000 1.00000
3.00000 1.00000
3.00000 0.00000
0 0

Sample Output

1.00000
分析：
凸多边形间最小距离 
给定两个非连接（比如不相交）的凸多边形 P 和 Q， 目标是找到拥有最小距离的点对 (p,
q) （p 属于 P 且 q 属于 Q）。   
 
事实上， 多边形非连接十分重要， 因为我们所说的多边形包含其内部。 如果多边形相交，
 那么最小距离就变得没有意义了。 然而， 这个问题的另一个版本， 凸多边形顶点对间最
小距离对于相交和非相交的情况都有解存在。  
 
回到我们的主问题： 直观的， 确定最小距离的点不可能包含在多边形的内部。 与最大距
离问题相似， 我们有如下结论：  
 
两个凸多边形 P 和 Q 之间的最小距离由多边形间的对踵点对确立。 存在凸多边形间的三
种多边形间的对踵点对， 因此就有三种可能存在的最小距离模式：  
1. “顶点-顶点”的情况  
2. “顶点-边”的情况  
3. “边-边”的情况  
 
换句话说， 确定最小距离的点对不一定必须是顶点。
考虑如下的算法， 算法的输入是两个分别有 m 和 n 个顺时针给定顶点的凸多边形 P 和
 Q。  
1. 计算 P 上 y 坐标值最小的顶点（称为 yminP ） 和 Q 上 y 坐标值最大的顶点（称
为 ymaxQ）。   
2. 为多边形在 yminP 和 ymaxQ 处构造两条切线 LP 和 LQ 使得他们对应的多边
形位于他们的右侧。 此时 LP 和 LQ 拥有不同的方向， 并且 yminP 和 ymaxQ 
成为了多边形间的一个对踵点对。  
3. 计算距离(yminP,ymaxQ) 并且将其维护为当前最小值。  
4. 顺时针同时旋转平行线直到其中一个与其所在的多边形的边重合。
5. 如果只有一条线与边重合， 那么只需要计算“顶点-边”对踵点对和“顶点-顶点”对踵点
对距离。 都将他们与当前最小值比较， 如果小于当前最小值则进行替换更新。 如果
两条切线都与边重合， 那么情况就更加复杂了。 如果边“交叠，”  也就是可以构造一
条与两条边都相交的公垂线（但不是在顶点处相交）， 那么就计算“边-边”距离。 否
则计算三个新的“顶点-顶点”对踵点对距离。 所有的这些距离都与当前最小值进行比
较， 若小于当前最小值则更新替换。  
6. 重复执行步骤4和步骤5， 直到新的点对为(yminP,ymaxQ)。  
7. 输出最大距离。  
旋转卡壳模式保证了所有的对踵点对（和所有可能的子情况）都被考虑到。 此外， 整个算
法拥有现行的时间复杂度， 因为（除了初始化）， 只有与顶点数同数量级的操作步数需要
执行。

#include <iostream>
#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

struct Point
{
	double x,y;
	Point() {}
	Point(double x,double y):x(x),y(y) {}
};

typedef Point Vector;
Vector operator +(Vector A,Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator -(Vector A,Vector B){return Vector(A.x-B.x,A.y-B.y);}
Vector operator *(Vector A,double p){return Vector(A.x*p,A.y*p);}
Vector operator /(Vector A,double p){return Vector(A.x/p,A.y/p);}
bool operator < (const Point &a,const Point &b)
{
    return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
const double eps=1e-10;
int dcmp(double x)
{
    if(fabs(x)<eps) return 0;
    else return x<0?-1:1;
}
bool operator == (const Point &a,const Point &b){
    return (dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0);
}
double Dot(Vector A,Vector B){return A.x*B.x+A.y*B.y;}
double Length(Vector A){return sqrt(Dot(A,A));}
double Angle(Vector A,Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}
double Cross(Vector A,Vector B){ return A.x*B.y-A.y*B.x;}
double min(double a,double b){ return a<b?a:b;}
double max(double a,double b){ return a>b?a:b;}
double Dist(Point a,Point b){ return Length(a-b);}

Point read_point()
{
	Point p;
	scanf("%lf %lf",&p.x,&p.y);
	return p;
}

double DistanceToSegment(Point p,Point a,Point b)//点到线段的距离
{
	if(a == b) return Length(p-a);
	Vector v1=b-a,v2=p-a,v3=p-b;
	if(dcmp(Dot(v1,v2)) < 0) return Length(v2);
	else if(dcmp(Dot(v1,v3)) > 0) return Length(v3);
	else return fabs(Cross(v1,v2))/Length(v1);
}

vector<Point> ConvexHull(vector<Point>& p) //求凸包
{
    sort(p.begin(), p.end());
    p.erase(unique(p.begin(), p.end()), p.end());
    int i,n = p.size();
    int m = 0;
    vector<Point> ch(n+1);
    for(i = 0; i < n; i++) {
        while(m > 1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
        ch[m++] = p[i];
    }
    int k = m;
    for(i = n-2; i >= 0; i--) {
        while(m > k && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
        ch[m++] = p[i];
    }
    if(n > 1) m--;
    ch.resize(m);
    return ch;
}

double DistSegToSeg(Point p0,Point p1,Point p2,Point p3)//两线段间的最小距离
{
    double ans1 = min(DistanceToSegment(p0,p2,p3),DistanceToSegment(p1,p2,p3));
    double ans2 = min(DistanceToSegment(p2,p0,p1),DistanceToSegment(p3,p0,p1));
    return min(ans1,ans2);
}

double Rotating_Calipers(vector<Point> p1,vector<Point> p2)//旋转卡壳算法凸包间的最小距离
{
	int s1=0,s2=0,n=p1.size(),m=p2.size(),i;
	p1.push_back(p1[0]);
	p2.push_back(p2[0]);
	double ans=1e10;
        int temp;
	for(i=0;i<n;i++)//找出p1凸包上y值最小的点
		if(dcmp(p1[i].y-p1[s1].y) < 0) s1=i;
        for(i=0;i<m;i++)//找出p2凸包上y值最大的点
			if(dcmp(p2[i].y-p2[s2].y) > 0) s2=i;
			for(i=0;i<n;i++)
			{
				while(temp=dcmp(Cross(p2[(s2+1)%m]-p2[s2],p2[s2]+p1[(s1+1)%n]-p1[s1]-p2[s2])) < 0)
					s2=(s2+1)%m;
                if(temp == 0)
					ans = min(ans,DistSegToSeg(p1[s1],p1[(s1+1)%n],p2[s2],p2[(s2+1)%m]));
                else ans = min(ans,DistanceToSegment(p2[s2],p1[s1],p1[(s1+1)%n]));
				s1 = (s1+1)%n;
			}
			return ans;
}

double solve(vector<Point> p1,vector<Point> p2)
{
	return min(Rotating_Calipers(p1,p2),Rotating_Calipers(p2,p1));
}

int main()
{
	int n,m,i;
	vector<Point> p1,p2;
	while(scanf("%d %d",&n,&m),n+m)
	{

		p1.clear();p2.clear();
		for(i=0;i<n;i++) p1.push_back(read_point());
		for(i=0;i<m;i++) p2.push_back(read_point());
		printf("%.5lf\n",solve(ConvexHull(p1),ConvexHull(p2)));
	}
	return 0;
}