hihoCoder1381 - Little Y's Tree

Description

给出一个$n(n\leq10^5)$个点的带边权的树。进行$Q$次询问：每次删除树上的$k$条边，求剩下的$k+1$个连通块中最远点对距离的和。$\Sigma k\leq10^5$，询问之间是独立的。

Solution

神奇而又毒瘤的做法。

考虑如何合并树上两个连通块的答案。设两个连通块的最远点对分别为$(v_1,v_2),(v_3,v_4)$，那么合并后的最远点对的两个端点一定是$\{v_1,v_2,v_3,v_4\}$中的两个。LCA用RMQ求的话时间复杂度是$O(1)$。

证明：

设两个连通块通过边$(p,q)$连通。若合并后的最远路径不经过$(p,q)$，则其一定是$(v_1,v_2),(v_3,v_4)$之一。若经过$(p,q)$，则可以将其看成$(u_1,p)+(p,q)+(q,u_2)$，而$(v_1,p),(v_2,p)$必然是以$p$为端点的最长、次长路径，所以$u_1$必然是$v_1,v_2$之一；$u_2$同理。

删除边$(u,v)$相当于将以$v$为根的子树从原树上断掉，断掉$k$条边相当于将原树变成了以$1$和$v_{1..k}$为根的$k+1$个连通块。那么做出原树的DFS序，断掉一个子树就相当于删掉一个区间。如图，子树$1$中的子树$2$和子树$6$被断掉，那么就删掉这两个区间，剩下的$\{1,3\}$即以$1$为根的连通块；同理$2$中的$4$被断掉，从$2$的DFS序中删掉$4$的就是$\{2,5\}$。

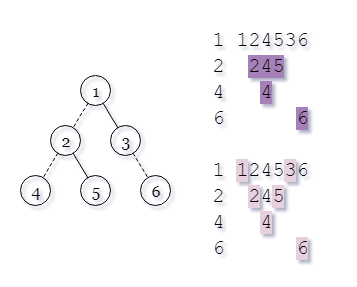
对所有区间排序并递归，可以求出每个连通块中有哪些点，那么该连通块中的最远点对相当于DFS序上的若干个区间的合并。由于新加入一个区间最多把原区间分成三份，所以最多要询问$2k+1$次。用线段树维护DFS序，每个节点记录该区间内的最远点对即可。虽然DFS上连续的点在原树上不一定连通，不过由于我们每次询问的部分都是连通的所以没关系啦。

时间复杂度$O(logn\Sigma k)$。

Code

//Little Y's Tree

#include <algorithm>

#include <cstdio>

using std::sort; using std::max; using std::swap;

typedef long long lint;

inline char gc()

{

    static char now[1<<16],*s,*t;

    if(s==t) {t=(s=now)+fread(now,1,1<<16,stdin); if(s==t) return EOF;}

    return *s++;

}

inline int read()

{

    int x=0; char ch=gc();

    while(ch<'0'||'9'<ch) ch=gc();

    while('0'<=ch&&ch<='9') x=x*10+ch-'0',ch=gc();

    return x;

}

const int N=1e5+10;

int n;

int cnt,h[N];

struct edge{int u,v,w,nxt;} ed[N<<1];

void edAdd(int u,int v,int w)

{

    cnt++; ed[cnt].u=u,ed[cnt].v=v,ed[cnt].w=w,ed[cnt].nxt=h[u],h[u]=cnt;

    cnt++; ed[cnt].u=v,ed[cnt].v=u,ed[cnt].w=w,ed[cnt].nxt=h[v],h[v]=cnt;

}

int fa[N],dpt[N]; lint dst[N];

int dfCnt1,dfn1[N],fr1[N],to1[N];

int dfCnt2,dfn2[N<<1],fr2[N];

void dfs(int u)

{

    dfn1[++dfCnt1]=u; fr1[u]=dfCnt1;

    dfn2[++dfCnt2]=u; fr2[u]=dfCnt2;

    for(int i=h[u];i;i=ed[i].nxt)

    {

        int v=ed[i].v,w=ed[i].w;

        if(v==fa[u]) continue;

        fa[v]=u,dpt[v]=dpt[u]+1,dst[v]=dst[u]+w;

        dfs(v); dfn2[++dfCnt2]=u;

    }

    to1[u]=dfCnt1;

}

int Lg2[N<<1],rmq[N<<1][20];

void bldLCA()

{

    Lg2[1]=0;

    for(int i=2;i<=dfCnt2;i++) Lg2[i]=Lg2[i>>1]+1;

    for(int i=1;i<=dfCnt2;i++) rmq[i][0]=dfn2[i];

    for(int k=1;k<=18;k++)

        for(int i=1;i+(1<<k-1)<=dfCnt2;i++)

        {

            int r1=rmq[i][k-1],r2=rmq[i+(1<<k-1)][k-1];

            rmq[i][k]=dpt[r1]<dpt[r2]?r1:r2;

        }

}

int lca(int u,int v)

{

    int i=fr2[u],j=fr2[v];

    if(i>j) swap(i,j);

    int t=Lg2[j-i+1];

    int r1=rmq[i][t],r2=rmq[j-(1<<t)+1][t];

    return dpt[r1]<dpt[r2]?r1:r2;

}

lint dist(int u,int v) {return dst[u]+dst[v]-2*dst[lca(u,v)];}

#define Ls (p<<1)

#define Rs (p<<1|1)

int rt=1; int maxP=0;

struct node

{

    lint len; int v1,v2;

    node(lint _len=0,int _v1=0,int _v2=0) {len=_len,v1=_v1,v2=_v2;}

}nd[N<<2];

node operator +(node x,node y)

{

    if(x.v1==0) return y; else if(y.v1==0) return x;

    node z=node(0,0,0);

    lint d[10],d0=0;

    d[1]=dist(x.v1,x.v2),d[2]=dist(x.v1,y.v1),d[3]=dist(x.v1,y.v2);

    d[4]=dist(x.v2,y.v1),d[5]=dist(x.v2,y.v2),d[6]=dist(y.v1,y.v2);

    for(int i=1;i<=6;i++) d0=max(d0,d[i]);

    if(d[1]==d0) z=node(d[1],x.v1,x.v2);

    else if(d[2]==d0) z=node(d[2],x.v1,y.v1);

    else if(d[3]==d0) z=node(d[3],x.v1,y.v2);

    else if(d[4]==d0) z=node(d[4],x.v2,y.v1);

    else if(d[5]==d0) z=node(d[5],x.v2,y.v2);

    else if(d[6]==d0) z=node(d[6],y.v1,y.v2);

    return z;

}

void update(int p) {nd[p]=nd[Ls]+nd[Rs];}

void bldTr(int p,int L0,int R0)

{

    maxP=max(maxP,p);

    if(L0==R0) {nd[p]=node(0,dfn1[L0],dfn1[L0]); return;}

    int mid=L0+R0>>1;

    bldTr(Ls,L0,mid),bldTr(Rs,mid+1,R0);

    update(p);

}

int optL,optR;

node query(int p,int L0,int R0)

{

    if(optL<=L0&&R0<=optR) return nd[p];

    int mid=L0+R0>>1; node res=node(0,0,0);

    if(optL<=mid) res=res+query(Ls,L0,mid);

    if(mid<optR) res=res+query(Rs,mid+1,R0);

    return res;

}

struct qRec{int fr,to; node ans;} q[N];

bool cmpQ(qRec x,qRec y) {return x.fr<y.fr;}

int m,now;

//solve(x)解决区间x及其内部区间，并将now移动到x外的第一个

void solve(int x)

{

    if(x>m) return;

    now++; int pre=q[x].fr;

    while(now<=m&&q[now].to<=q[x].to)

    {

        optL=pre,optR=q[now].fr-1;

        if(optL<=optR) q[x].ans=q[x].ans+query(rt,1,n);

        pre=q[now].to+1;

        solve(now);

    }

    optL=pre,optR=q[x].to;

    if(optL<=optR) q[x].ans=q[x].ans+query(rt,1,n);

}

int main()

{

    n=read();

    for(int i=1;i<=n-1;i++)

    {

        int u=read(),v=read(),w=read();

        edAdd(u,v,w);

    }

    fa[1]=0,dfs(1);

    bldLCA(); bldTr(rt,1,n);

    int Q=read();

    while(Q--)

    {

        m=read();

        for(int i=1;i<=m;i++)

        {

            int x=read()<<1; int u=ed[x].u,v=ed[x].v;

            if(dpt[u]>dpt[v]) swap(u,v);

            q[i].fr=fr1[v],q[i].to=to1[v];

            q[i].ans=node(0,0,0);

        }

        m++; q[m].fr=1,q[m].to=n,q[m].ans=node(0,0,0);

        sort(q+1,q+m+1,cmpQ);

        solve(now=1);

        lint res=0;

        for(int i=1;i<=m;i++) res+=(q[i].ans).len;

        printf("%lld\n",res);

    }

    return 0;

}

P.S.

Icefox不到100行orz，我写了150+