URAL 2031. Overturned Numbers （枚举）

2031. Overturned Numbers

Time limit: 1.0 second

Memory limit: 64 MB

Little Pierre was surfing the Internet and came across an interesting puzzle:

What is the number under the car?

It took some time before Pierre solved the puzzle, but eventually he understood that there were overturned numbers 86, 88, 89, 90, and 91 in the picture and the answer was the number 87.

Now Pierre wants to entertain his friends with similar puzzles. He wants to construct a sequence of
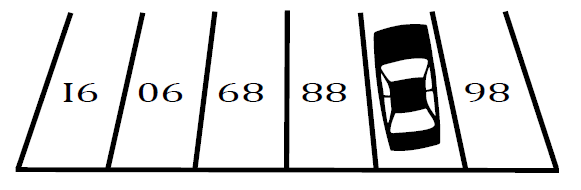
n numbers such that its overturning produces a consecutive segment of the positive integers. Pierre intends to use one-digit integers supplemented with a leading zero and two-digit integers only.To avoid ambiguity, note that when the digits 0, 1, and
8 are overturned, they remain the same, the digits 6 and 9 are converted into each other, and the remaining digits become unreadable symbols.

Input

The only line contains the number n of integers in a sequence (1 ≤
n ≤ 99).

Output

If there is no sequence of length n with the above property, output “Glupenky Pierre” (“Silly Pierre” in Russian).Otherwise, output any of such sequences. The numbers in the sequence should be separated with a space.

Samples

input	output
2	11 01
99	Glupenky Pierre

Problem Author: Nikita Sivukhin

Problem Source: Ural Regional School Programming Contest 2014

解析：题目要求翻转后为连续序列的序列，直接枚举就可以。

AC代码：

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n;
    while(scanf("%d", &n) != EOF){
        if(n == 1) puts("01");
        else if(n == 2) puts("11 01");
        else if(n == 3) puts("06 68 88");
        else if(n == 4) puts("16 06 68 88");
        else puts("Glupenky Pierre");
    }
    return 0;
}