leetcode_1039. Minimum Score Triangulation of Polygon_动态规划

https://leetcode.com/problems/minimum-score-triangulation-of-polygon/

题意：给定一个凸的N边形(N<=50)，每个顶点有一个权值A[i]，把它分为N-2个三角形，每个三角形的val等于三个顶点的权值的乘积，问划分之后图形的val总和最小为多少。

---

一开始想到了，问题可以转换为求解子问题，由于没有想到如何进行状态转换，并且感觉贪心可行，

如下图1，将当前图形可以构成的三角形找出（红线为底边），从中找到val最小的三角形如图2，然后将其割除如图3，再将新的两个三角形找出。

   

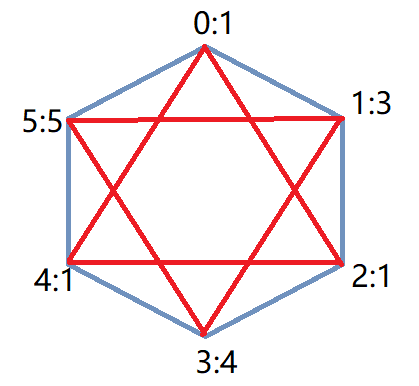
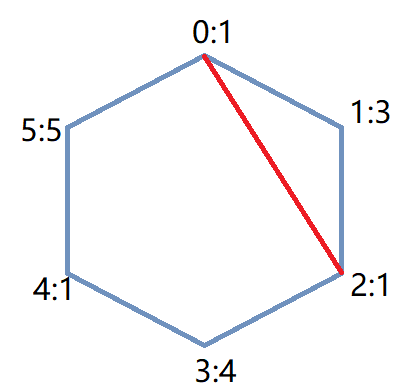
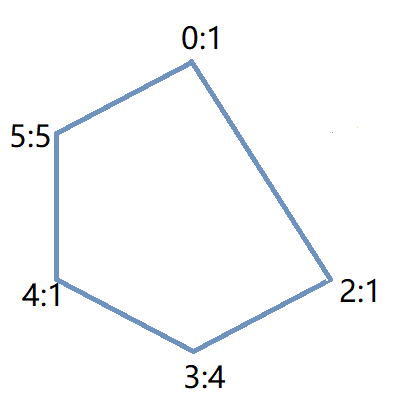
然而这个思路并不可行，这个思路的局部最优并不能得到全局最优，按照上面的思路的策略如下图，得到结果40，而最优解是24。

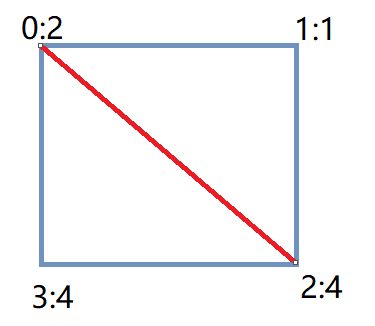
贪心不可行，每次找到最优的三角形，最终全局未必最优。

---

然后，想到很可能是动态规划，但是想不出来，问题如何分解，状态如何表示。。。

参考别人的思路和代码（看了两个大佬的代码，思路几乎一样）

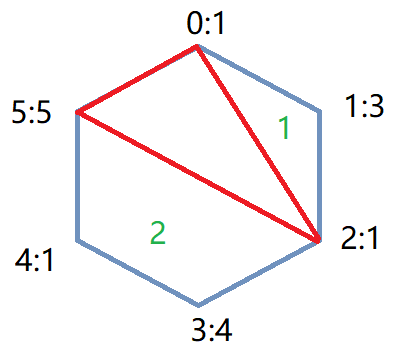
对于多边形上的任意一条边，它只能出现在一个三角形中，

dp[i][j]：从第i个点到第j个点的最小值。dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j]+A[i]*A[j]*A[k])。

如下图：此时求dp[0][5]，以（0,5）为边，在（0,5）之间遍历三角形的顶点，构成的每个三角形将原图形分为三部分：三角形，子图形1，子图形2。

class Solution
{
public:
    int minScoreTriangulation(vector<int>& A)
    {
        int dp[][];
        memset(dp,,sizeof(dp));
        int numofnode = A.size();
        for(int len=; len<=numofnode; len++)
            for(int i=; i+len-<numofnode; i++)
            {
                int j=i+len-;
                dp[i][j]=INT_MAX;
                for(int k=i+; k<j; k++)
                    dp[i][j] = min(dp[i][j],dp[i][k]+dp[k][j]+A[i]*A[j]*A[k]);
            }
        return dp[][A.size()-];
    }
};