AcWing - 闫氏DP分析法

核心思想：从集合角度来分析DP问题

在我们遇到的DP问题中，一般都是求在一个有限集内的最值，但是这些方案数量一般都是指数级别的，想要一个一个查找出来不太可能。所以DP方法是用来优化这种寻找最优方案的过程的。

DP问题一般来说分析时都要经过两个阶段：

1. 状态表示（化零为整）：指把一些具有相似点的方案，划分为一个子集，然后用一个状态来表示它。现在假设我们的状态表示为 \(f[i]\)。

   状态表示要从两个角度来分析：

   1. 集合：\(f[i]\) 表示的集合就是：所有满足xxx条件的集合。正是因为我们的 \(f[i]\) 可以表示一类东西而不是一个东西，这样就可以达到优化的作用。
   2. 属性：也就是我们状态存的这个值是这个集合的什么东西，也就是最大值/最小值/数量等等。

2. 状态计算（化整为零）：先看一下 \(f[i]\) 表示的所有状态是什么：

   比如说是这个集合：

   

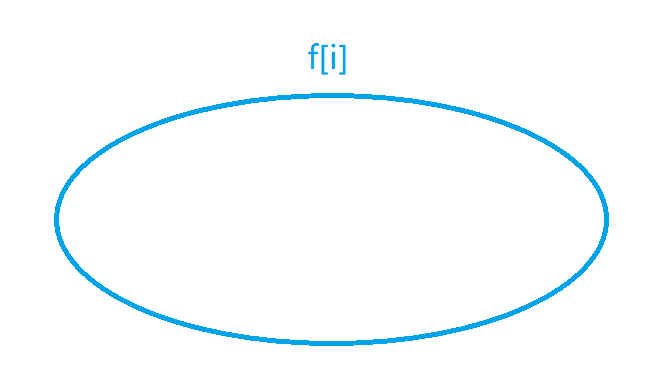
   然后把它划分成一个个子集（如果求的是数量那么必须不重复；如果求的是最大值就不用管了），我们的划分依据是：寻找最后一个不同点。

   

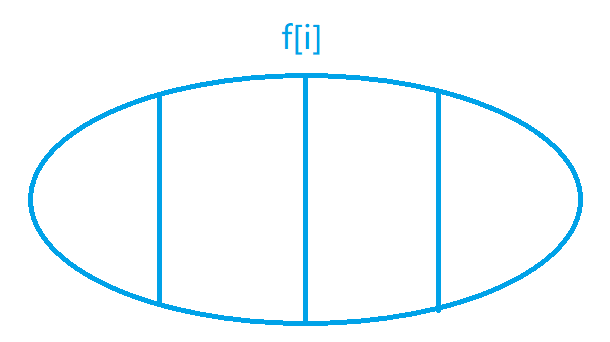
   如果要求整个状态的最大值的话，我们只需要把这个状态的所有子集的最大值求出来，再把整个集合的最大值求出来就可以了。这样，我们就成功把一个大问题分解成一个个小问题求解出来了。

举例：01背包问题

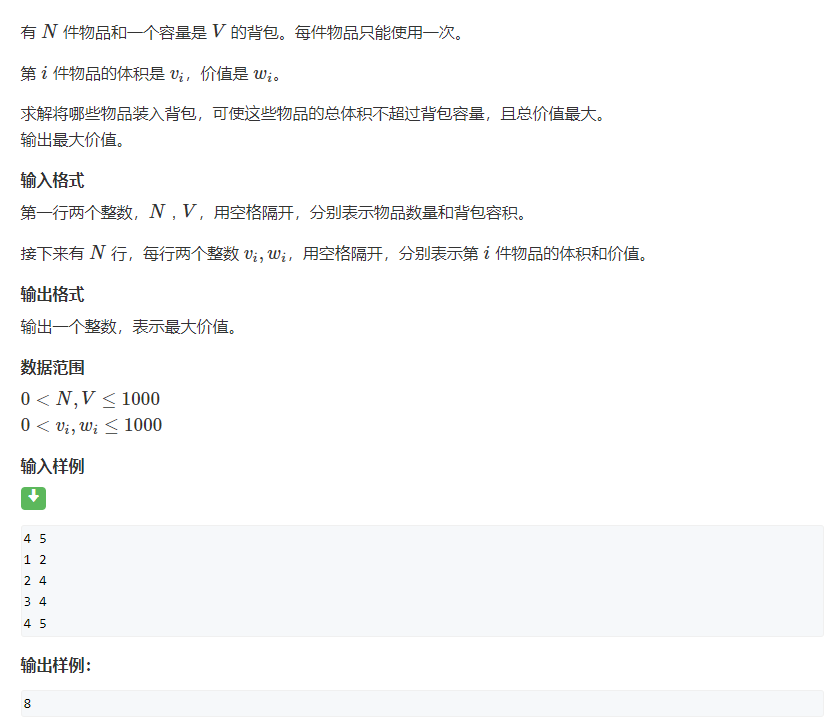
开始使用闫氏DP分析法！

1. 状态表示：\(f[i][j]\)

   1. 集合：所有只考虑前 \(i\) 个物品，且总体积不超过 \(j\) 的选法的集合。
   2. 属性：Max（最大值）

2. 状态计算：

   

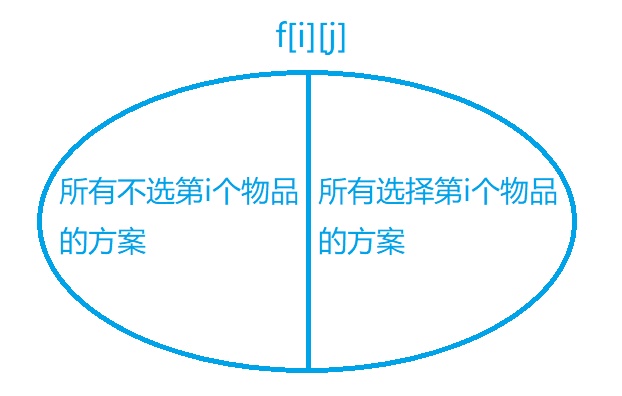
   想要取得最大值，只需要得出左边集合的最大值和右边集合的最大值就可以了。

   我们来看一下这两个子集分别是什么

   

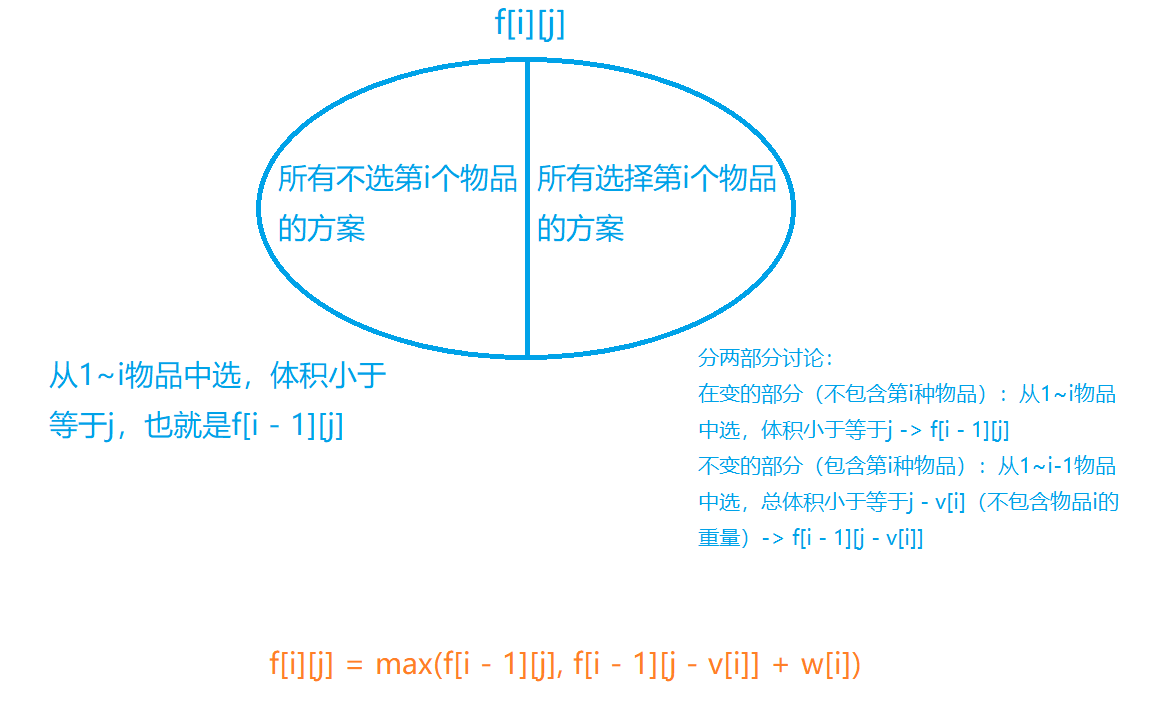
   完成！这样我们就成功地把这个问题推出来了。

这个问题还可以再继续优化，目前的状态表示是二维的，但是每次我们只会用到第 \(i - 1\) 层的东西，这样就可以用滚动数组来优化了。还有，我们的状态表示的第二维要么是用自己，要么是用比自己小的数，我们就可以从大到小枚举体积，换为一维数组来存储状态。

为什么可以这样呢？如果用一维数组来存储状态，状态转移方程就是这样了：

\(f[j] = max(f[j], f[j - v[i]] +w[i])\)

因为我们是从大到小枚举体积，所以这时的 \(f[j - v[i]]\) 还没有在第 \(i\) 层被更新过；所以此时它存的就是上一层的 \(f[j - v[i]]\)，也就是 \(f[i - 1][j - v[i]]\)。

代码：

朴素版

#include <iostream>
#define N 1010
using namespace std;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
	for (int i = 1; i <= n; ++i)
		for (int j = 0; j <= m; ++j) {
			f[i][j] = f[i - 1][j]; // 左半边的子集
			if (j >= v[i]/*右半边的方案是存在的*/) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
		}
	cout << f[n][m] << '\n';
	return 0;
}

优化版

#include <iostream>
#define N 1010
using namespace std;
int n, m;
int v[N], w[N];
int f[N];
int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
	for (int i = 1; i <= n; ++i)
		for (int j = m; j >= v[i]/*就相当于在循环里判断一句j >= v[i]*/; --j)
			f[j] = max(f[j], f[j - v[i]] + w[i]);
	cout << f[m] << '\n';
	return 0;
}

有了闫氏DP分析法，从此再也不怕DP问题！