洛谷P1009 阶乘之和

捏妈第三节的题单名不是循环结构吗，直接出了第八节的高精度大数计算，紧急学习

对于较大数的加减乘除阶乘等，C/C++原生的数据类型是存储不了的（即便用longlong）,直接计算会出现数据移除成负数的结果

为了解决这类超大数的运算，我们选择用字符数组或者整型数组来进行模拟运算。

所谓模拟运算也就是把大数的每一位存储到数组的一个数组元素中，然后模拟类似于列竖式手算的形式来一位一位的进行运算

最后输出的时候当然也是一位一位的输出了，而且为了计算进位方便，通常倒序存储数字，同时输出时倒序输出

P1009d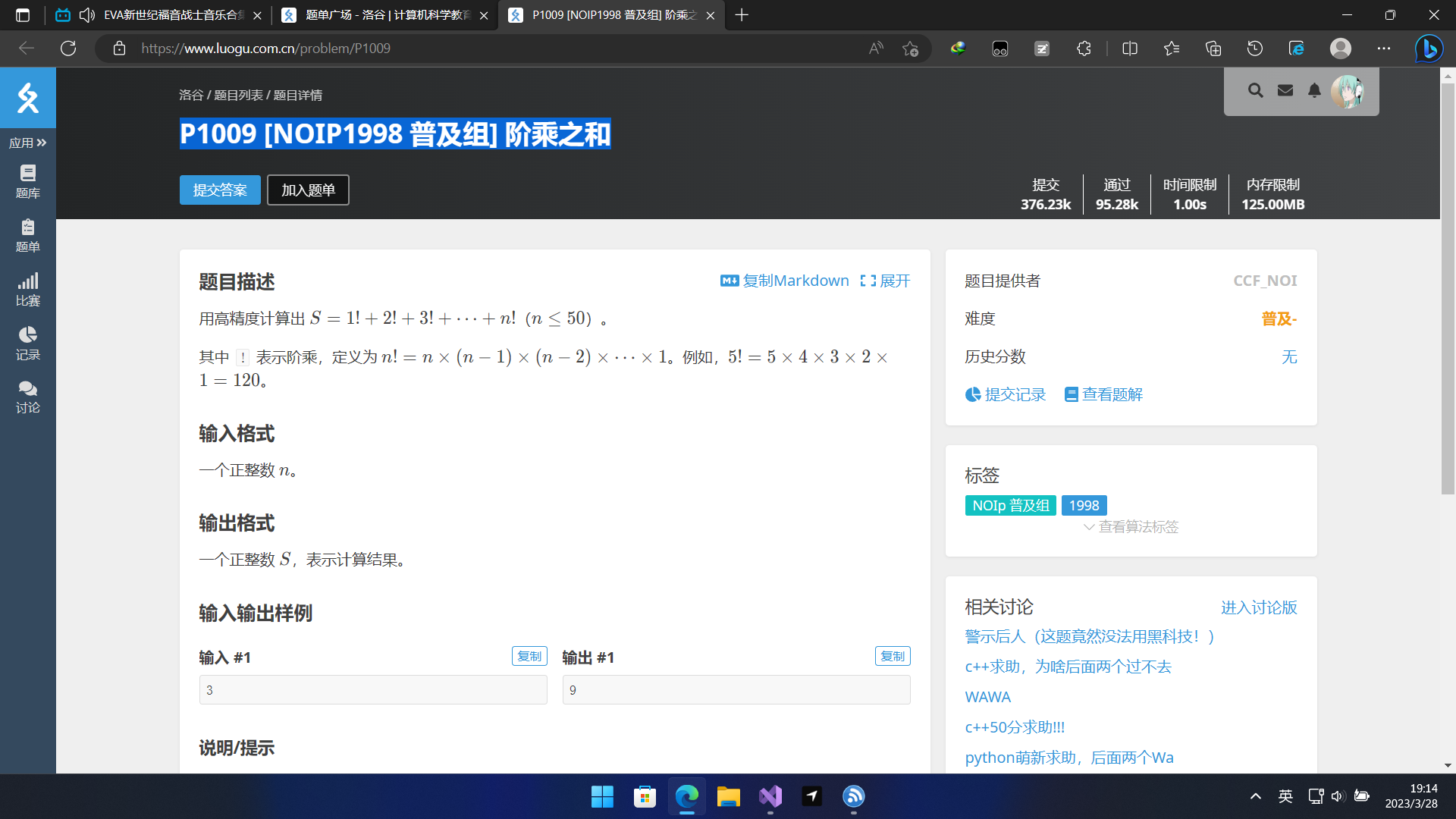

这道题其实就是让我们用高精度阶乘加上高精度加法来算结果

 1 #include<stdio.h>
 5 int main()
 6 {
 7     int N;
 8     scanf("%d", &N);//阶乘指标输入
 9     int Factorial[1000] = { 0 };//Factorial,阶乘的英语，嘿嘿

//这个数组用来存储每次阶乘的结果

10     Factorial[0] = 1;//初始化
11     int Num = 0;//进位指示，初始无进位数据
12     int Digit = 1;//当前数组或者说大数的位数,同时也可以作为逆序输出的指针

14     for (int i = 1; i <= N; i++)
15     {
16         for (int j = 0; j <Digit; j++)
17         {
18             int Temp = Factorial[j] * i + Num;//临时数据存储，包含计算数据以及上次保存的进位数据
19             Factorial[j] = Temp % 10;
20             Num = Temp / 10;//将个位存入当前位的数组，十位的数字存入进位指示进入下一轮
21         }
22         while(Num)//进位数据若未取完，说明要顺延进位
23         {
24             Factorial[Digit] = Num%10;
25             Num = Num / 10;//对于百位及以上未取完进位数据的处理,因为乘法进位可能会超过十位，这一点加法就不用考虑了
26             Digit++;//进位，位数加一
27         }
28     }
29     for (int i = Digit - 1; i >= 0; i--)//以Digit为倒序指针来倒序输出
30     {
31         printf("%d", Factorial[i]);
32     }
33     return 0;
34 }

上面是独立的大数阶乘实现，由于是从已知数一步一步累乘，所以比大数乘法实现更简洁简单

下面是阶乘整合大数的加法

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int* Factor(int N,int* Digit)
{
    int* Factorial = (int*)malloc(sizeof(int) * 1000);//堆上申请便于返回！！！，刚开始我是申请在栈上的数组，出错了wwww
    memset(Factorial, 0, sizeof(Factorial));//赋值0
    Factorial[0] = 1;//初始化
    int Num = 0;//进位指示，初始无进位数据
    //这个数组用来存储每次阶乘的结果
    for (int i = 1; i <= N; i++)
    {
        for (int j = 0; j < *Digit; j++)
        {
            int Temp = Factorial[j] * i + Num;//临时数据存储，包含计算数据以及上次保存的进位数据
            Factorial[j] = Temp % 10;
            Num = Temp / 10;//将个位存入当前位的数组，十位的数字存入进位指示进入下一轮
        }
        while (Num)//进位数据若未取完，说明要顺延进位
        {
            Factorial[*Digit] = Num % 10;
            Num = Num / 10;//对于百位及以上未取完进位数据的处理
            (* Digit)++;//进位，位数加一
        }
    }

    return Factorial;

}
int main()
{
    int N;
    scanf("%d", &N);//阶乘指标输入
    int Sum[1000] = { 0 };
    for (int i = 1; i <= N; i++)
    {
        int Digit = 1;
        int* F = Factor(i,&Digit);
        int Num = 0;//与上述阶乘实现一样， Num依旧为进位指标
        for (int k = 0; k < Digit;k++)
        {
            int Temp = F[k] + Sum[k]+Num;//两数相加再加上上一轮继承来的进位数
            Sum[k] = Temp % 10;//取个位
            Num = Temp / 10;//取十位
        }
        if (Num)
        {
            Sum[Digit] += Num;
            Num = 0;//在仅考虑十位进制的情况下可以更简单的处理
        }
        free(F); F = NULL;//内存回收
    }
    int k = 999;
    for (; !Sum[k]; k--);//过滤掉前导的0
    for (; k >= 0; k--)
    {
        printf("%d", Sum[k]);
    }
    return 0;
}