算法练习(19)-单源最短路径dijkstra算法

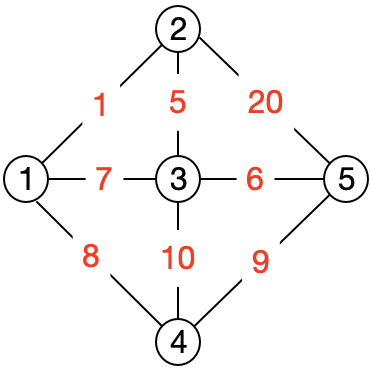
如上图，先初始化1个图，每条边上的红色数字为路径权重：（Node,Edge的定义参见算法练习(17)-图的广度优先遍历/深度优先遍历）

Graph init() {
        List<Node> nodes = new ArrayList<>();
        List<Edge> edges = new ArrayList<>();

        Node n1 = new Node(1);
        Node n2 = new Node(2);
        Node n3 = new Node(3);
        Node n4 = new Node(4);
        Node n5 = new Node(5);

        nodes.add(n1);
        nodes.add(n2);
        nodes.add(n3);
        nodes.add(n4);
        nodes.add(n5);

        Edge e_1_2 = new Edge(1, n1, n2);
        Edge e_2_1 = new Edge(1, n2, n1);
        Edge e_1_3 = new Edge(7, n1, n3);
        Edge e_3_1 = new Edge(7, n3, n1);
        Edge e_1_4 = new Edge(8, n1, n4);
        Edge e_4_1 = new Edge(8, n4, n1);
        Edge e_2_3 = new Edge(5, n2, n3);
        Edge e_3_2 = new Edge(5, n3, n2);
        Edge e_3_4 = new Edge(10, n3, n4);
        Edge e_4_3 = new Edge(10, n4, n3);
        Edge e_2_5 = new Edge(20, n2, n5);
        Edge e_5_2 = new Edge(20, n5, n2);
        Edge e_5_4 = new Edge(9, n5, n4);
        Edge e_4_5 = new Edge(9, n4, n5);
        Edge e_3_5 = new Edge(6, n3, n5);
        Edge e_5_3 = new Edge(6, n5, n3);

        n1.edges.add(e_1_2);
        n1.edges.add(e_1_3);
        n1.edges.add(e_1_4);

        n2.edges.add(e_2_1);
        n2.edges.add(e_2_3);
        n2.edges.add(e_2_5);

        n3.edges.add(e_3_1);
        n3.edges.add(e_3_2);
        n3.edges.add(e_3_4);
        n3.edges.add(e_3_5);

        n4.edges.add(e_4_1);
        n4.edges.add(e_4_3);
        n4.edges.add(e_4_5);

        n5.edges.add(e_5_2);
        n5.edges.add(e_5_3);
        n5.edges.add(e_5_4);

        edges.add(e_1_2);
        edges.add(e_2_1);
        edges.add(e_1_3);
        edges.add(e_3_1);
        edges.add(e_1_4);
        edges.add(e_4_1);
        edges.add(e_2_3);
        edges.add(e_3_2);
        edges.add(e_3_4);
        edges.add(e_4_3);
        edges.add(e_2_5);
        edges.add(e_5_2);
        edges.add(e_5_4);
        edges.add(e_4_5);
        edges.add(e_3_5);
        edges.add(e_5_3);

        Graph g = new Graph(nodes, edges);
        return g;
    }

假设从节点1出发，到达其它节点的最短路径(权重)为：

出发点	目的地	最短路径(权重)和	全路径
1	1	0	1->1
1	2	1	1->2
1	3	1+5	1->2->3
1	4	8	1->4
1	5	1+5+6	1->2->3->5

package advanced;

import java.util.*;

public class GraphTest {

    Graph init() {
        ... 略...
    }

    /**
     * dijkstra算法
     * @param head
     * @return
     */
    Map<Node, Integer> dijkstra(Node head) {
        /**
         * 用于保存从head到其它node的距离总和
         * 不在该map中节点，表示还没走到，默认距离为正无穷
         */
        Map<Node, Integer> distanceMap = new HashMap<>();
        //首节点：从head到head的距离为0
        distanceMap.put(head, 0);
        //已经计算过的节点
        Set<Node> selectedNodes = new HashSet<>();
        //从出发点，找出距离最短的节点
        Node minNode = getMinDistanceNode(distanceMap, selectedNodes);
        while (minNode != null) {
            int distance = distanceMap.get(minNode);
            for (Edge edge : minNode.edges) {
                Node toNode = edge.to;
                if (!distanceMap.containsKey(toNode)) {
                    distanceMap.put(toNode, distance + edge.weight);
                }
                //取最短距离，更新distanceMap
                distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight));
            }
            //已计算过的节点，做下标识
            selectedNodes.add(minNode);
            minNode = getMinDistanceNode(distanceMap, selectedNodes);
        }
        return distanceMap;
    }

    /**
     * 从distanceMap中找出最小距离的节点（已计算过的节点忽略）
     * @param distanceMap
     * @param touchedNodes
     * @return
     */
    Node getMinDistanceNode(Map<Node, Integer> distanceMap,
                            Set<Node> touchedNodes) {
        Node minNode = null;
        int minDistance = Integer.MAX_VALUE;
        for (Map.Entry<Node, Integer> entry : distanceMap.entrySet()) {
            Node node = entry.getKey();
            int distance = entry.getValue();
            if (!touchedNodes.contains(node) && distance < minDistance) {
                minNode = node;
                minDistance = distance;
            }
        }
        return minNode;
    }

    public static void main(String[] args) {
        GraphTest t = new GraphTest();
        Graph g = t.init();
        Map<Node, Integer> dijkstra = t.dijkstra(g.nodes.get(0));
        System.out.println(dijkstra);
    }

}

输出：

{3=6, 4=8, 1=0, 5=12, 2=1}

注意：这个算法，有一个前提条件，如果图中有环，环上的路径合不能为负值，否则会在环里转来转去，每转一圈，路径合更小，一直循环，转不出来。

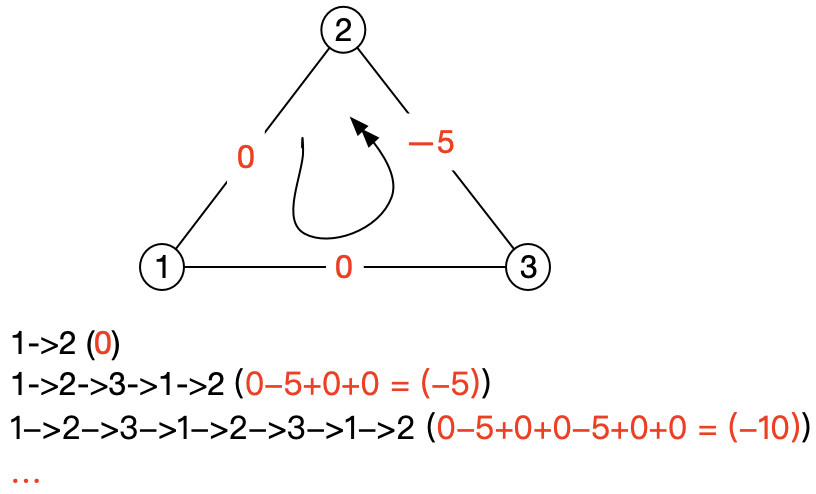
如上图，如果从1出发，要计算到节点2的最短路径，每转一圈，总路径反而更短。这种情况下，可以将所有边上的权重加“最大负权重”，将所有边上的权重变成非负值。