Codeforces Round 895 (Div. 3)

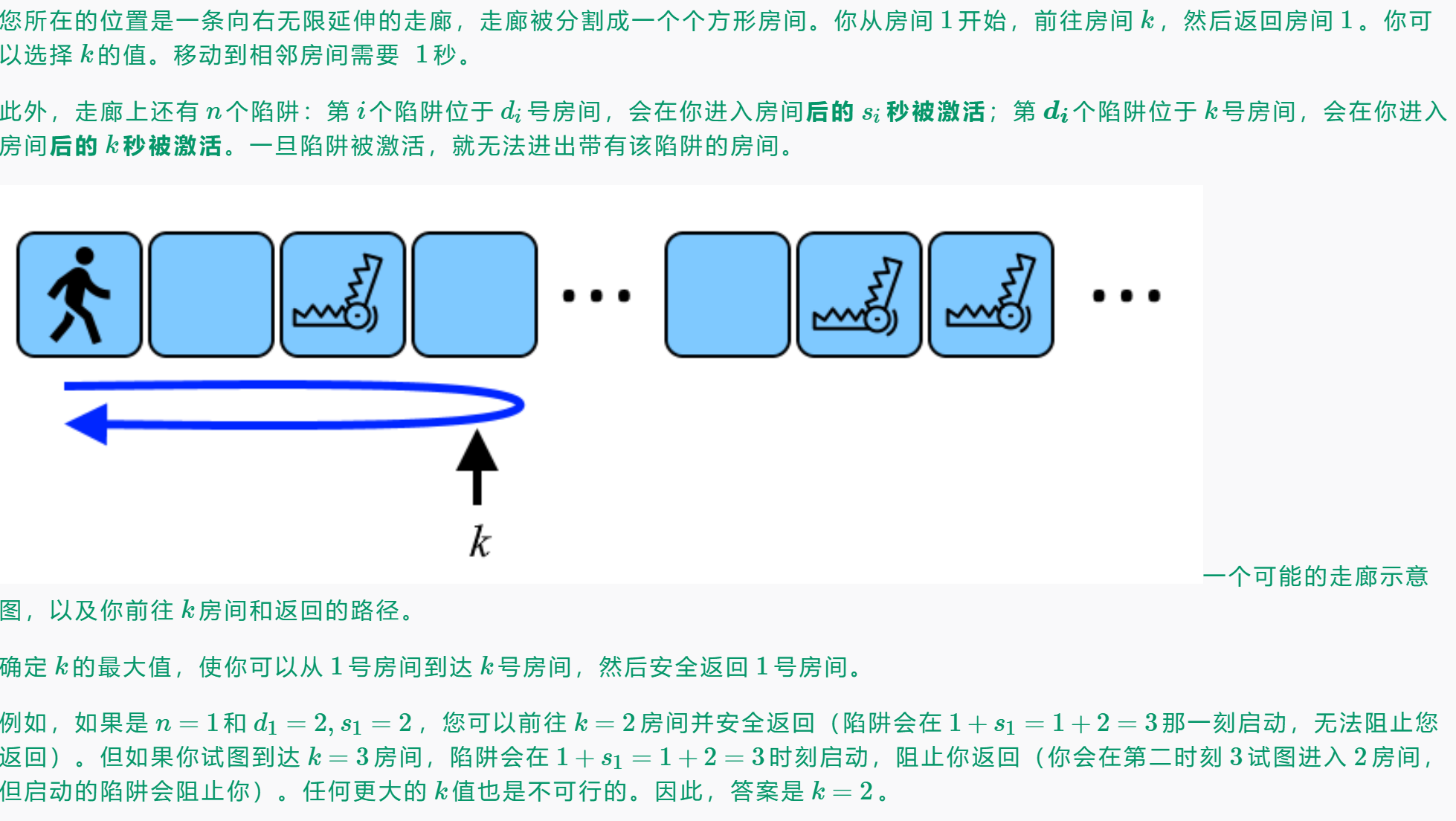
B. The Corridor or There and Back Again

题解

• 考虑二分答案
• \(check\)时判断是否\(s_i \leq 2*(k - d_i),k\geq d_i\)

const int N = 2e5 + 10, M = 4e5 + 10;

int n, d[N], s[N];

bool check(int mid)
{
    for (int i = 1; i <= n; ++i)
    {
        if (d[i] <= mid)
        {
            if (s[i] <= 2 * (mid - d[i]))
                return false;
        }
    }
    return true;
}

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> d[i] >> s[i];
    int l = 1, r = 1e15;
    while (l <= r)
    {
        int mid = l + r >> 1;
        if (check(mid))
            l = mid + 1;
        else
            r = mid - 1;
    }
    cout << r << endl;
}

C. Non-coprime Split

题解

• 容易发现一个大于1的非质数\(x\)一定可以由其约数\(y\)和\(x - y\)相加得到，且\(gcd(x-y,y)\neq1\)
• 直接暴力找大于1的非质数即可

const int N = 2e5 + 10, M = 4e5 + 10;

bool is_prime(int x, int &b)
{
    if (x < 2)
        return false;
    for (int i = 2; i <= x / i; ++i)
    {
        if (x % i == 0)
        {
            b = i;
            return false;
        }
    }
    return true;
}

void solve()
{
    int l, r;
    cin >> l >> r;
    int res = INF;
    int b = -1;
    for (int i = l; i <= r; ++i)
    {
        if (!is_prime(i, b) && i > 2)
        {
            res = i;
            break;
        }
    }
    if (res == INF)
        cout << -1 << endl;
    else
    {
        cout << b << " " << res - b << endl;
    }
}

D. Plus Minus Permutation

题解

• 贪心考虑，对于整除\(x\)的位置一定从\(n\)开始放，对于整除\(y\)的位置一定从\(1\)开始放
• 但是存在同时整除\(x\)和\(y\)的情况
• 求出\(lcm(x,y)\)，即可得到重合的位置数量\(n/lcm(x,y)\)
• 减去重合的位置数量后等差数列求和即可

const int N = 2e5 + 10, M = 4e5 + 10;

int n, x, y;

void solve()
{
    cin >> n >> x >> y;
    int t1 = n / x, t2 = n / y;
    int lc = lcm(x, y);
    int t3 = n / lc;
    t1 -= t3, t2 -= t3;
    cout << (n - t1 + 1 + n) * t1 / 2 - (1 + t2) * t2 / 2 << endl;
}

E. Data Structures Fan

题解

• 不会思维，赛时直接上线段树了
• 线段树维护区间二进制为\(0\)的位置上的异或和\(ans0\)，区间二进制为\(0\)的位置上的异或和\(ans1\)
• 考虑区间反转操作：直接交换\(ans0\)和\(ans1\)即可，并打上懒惰标记

const int N = 1e5 + 10, M = 4e5 + 10;

int n, q, a[N];
string s;
struct info
{
    int ans0, ans1;
    friend info operator+(const info &a, const info &b)
    {
        info c;
        c.ans0 = a.ans0 ^ b.ans0;
        c.ans1 = a.ans1 ^ b.ans1;
        return c;
    }
};
struct SEG
{
    int lazy;
    info val;
} seg[N << 2];

void up(int id)
{
    seg[id].val = seg[lson].val + seg[rson].val;
}

void settag(int id, int tag)
{
    swap(seg[id].val.ans0, seg[id].val.ans1);
    seg[id].lazy ^= tag;
}

void down(int id)
{
    if (seg[id].lazy == 0)
        return;
    settag(lson, seg[id].lazy);
    settag(rson, seg[id].lazy);
    seg[id].lazy = 0;
}

void build(int id, int l, int r)
{
    seg[id].lazy = 0;
    if (l == r)
    {
        if (s[l] == '1')
        {
            seg[id].val.ans0 = 0;
            seg[id].val.ans1 = a[l];
        }
        else
        {
            seg[id].val.ans0 = a[l];
            seg[id].val.ans1 = 0;
        }
        return;
    }
    int mid = l + r >> 1;
    build(lson, l, mid);
    build(rson, mid + 1, r);
    up(id);
}

void modify(int id, int l, int r, int ql, int qr, int tag)
{
    if (ql <= l && r <= qr)
    {
        settag(id, tag);
        return;
    }
    down(id);
    int mid = l + r >> 1;
    if (qr <= mid)
        modify(lson, l, mid, ql, qr, tag);
    else if (ql > mid)
        modify(rson, mid + 1, r, ql, qr, tag);
    else
    {
        modify(lson, l, mid, ql, qr, tag);
        modify(rson, mid + 1, r, ql, qr, tag);
    }
    up(id);
}

info query(int id, int l, int r, int ql, int qr)
{
    if (ql <= l && r <= qr)
        return seg[id].val;
    down(id);
    int mid = l + r >> 1;
    if (qr <= mid)
        return query(lson, l, mid, ql, qr);
    else if (ql > mid)
        return query(rson, mid + 1, r, ql, qr);
    else
        return query(lson, l, mid, ql, qr) + query(rson, mid + 1, r, ql, qr);
}

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];
    cin >> s;
    s = " " + s;
    build(1, 1, n);
    cin >> q;
    while (q--)
    {
        int op, l, r, g;
        cin >> op;
        if (op == 1)
        {
            cin >> l >> r;
            modify(1, 1, n, l, r, 1);
        }
        else
        {
            cin >> g;
            if (g == 0)
                cout << query(1, 1, n, 1, n).ans0 << " ";
            else
                cout << query(1, 1, n, 1, n).ans1 << " ";
        }
    }
    cout << endl;
}

F. Selling a Menagerie

题解

• 跑个拓扑排序，不在环上的随便放，然后对每个环上的从每个起点都跑一次找到贡献最大的起点
• 枚举起点的过程类似滑动窗口更新即可
• 可以断环成链方便一点

const int N = 1e5 + 10, M = 4e5 + 10;

int n, a[N], c[N], deg[N], vis[N], b[N];
vector<int> g[N];

void dfs(int u, vector<int> &vec)
{
    vis[u] = true;
    vec.push_back(u);
    for (auto v : g[u])
    {
        if (!vis[v])
            dfs(v, vec);
    }
}

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        g[i].clear(), deg[i] = vis[i] = 0;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
        g[i].push_back(a[i]);
        deg[a[i]]++;
    }
    for (int i = 1; i <= n; ++i)
        cin >> c[i];
    queue<int> q;
    for (int i = 1; i <= n; ++i)
    {
        if (deg[i] == 0)
            q.push(i);
    }
    vector<int> ans;
    while (q.size())
    {
        int u = q.front();
        vis[u] = true;
        q.pop();
        ans.push_back(u);
        for (auto v : g[u])
        {
            if (--deg[v] == 0)
                q.push(v);
        }
    }

    for (int i = 1; i <= n; ++i)
    {
        vector<int> vec;
        if (vis[i])
            continue;
        if (!vis[i])
            dfs(i, vec);
        int mx = 0, pos = 1, idx = 0;
        for (auto x : vec)
            b[++idx] = x;
        for (int i = 1; i <= idx; ++i)
            b[i + idx] = b[i];
        int sum = 0;
        for (int i = 1; i <= idx - 1; ++i)
            sum += 2 * c[b[i]];
        sum += c[b[idx]];
        mx = sum;
        for (int i = 2; i <= idx; ++i)
        {
            sum -= c[b[i - 1]];
            sum += c[b[i + idx - 1 - 1]];
            if (mx < sum)
            {
                sum = mx;
                pos = i;
            }
        }
        for (int i = pos; i <= pos + idx - 1; ++i)
            ans.push_back(b[i]);
    }
    for (auto u : ans)
        cout << u << " ";
    cout << endl;
}

G. Replace With Product

题解

• 首先序列两边的\(1\)完全可以用来加，所以我们处理出左边第一个不是\(1\)的位置\(l\)，同理处理出\(r\)
• 从位置\(l\)开始乘，设\(res\)为乘积
• 如果乘到某个位置\(x\)时\(res\geq 1e9\)，容易证明：对于区间\([x + 1, r]\)里面的数字，乘起来的和一定由于加起来的和
• 所以\([l,r]\)这段区间我们可以全选
• 如果最终\(res < 1e9\)，说明\(\geq 2\)的数的个数小于\(m = log(1e9)\)个，直接\(O(m^2)\)暴力枚举选择哪段区间为乘积即可
• 后面的过程模拟即可，注意区间中存在\(1\)，模拟时注意细节即可

const int N = 2e5 + 10, M = 4e5 + 10;

int n, a[N], b[N], idx;

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> a[i];

    int l = 1, r = n;
    while (a[l] == 1 && l < r)
        l++;
    while (a[r] == 1 && l < r)
        r--;
    int res = 1;
    for (int i = l; i <= r; ++i)
    {
        res *= a[i];
        if (res > 1e9)
        {
            cout << l << " " << r << endl;
            return;
        }
    }

    idx = 0;
    int sum = 0;
    for (int i = 1; i <= n; ++i)
    {
        if (a[i] > 1)
            b[++idx] = i;
        sum += a[i];
    }
    int ans = sum, ansl = 1, ansr = 1;
    for (int i = 1; i <= idx; ++i)
    {
        res = 1;
        l = b[i];
        int s = 0;
        for (int j = i; j <= idx; ++j)
        {
            res *= a[b[j]];
            r = b[j];
            s += a[b[j]];
            int val = sum - s - (r - l + 1 - (j - i + 1)) + res;
            if (val > ans)
            {
                ans = val;
                ansl = l, ansr = r;
            }
        }
    }
    cout << ansl << " " << ansr << endl;
}