Ai数学基础

数学基础

1.梯度

1.1偏导数

1.1.1定义

1.1.2几何意义

1.2方向导数

1.2.1定义

1.2.2定理

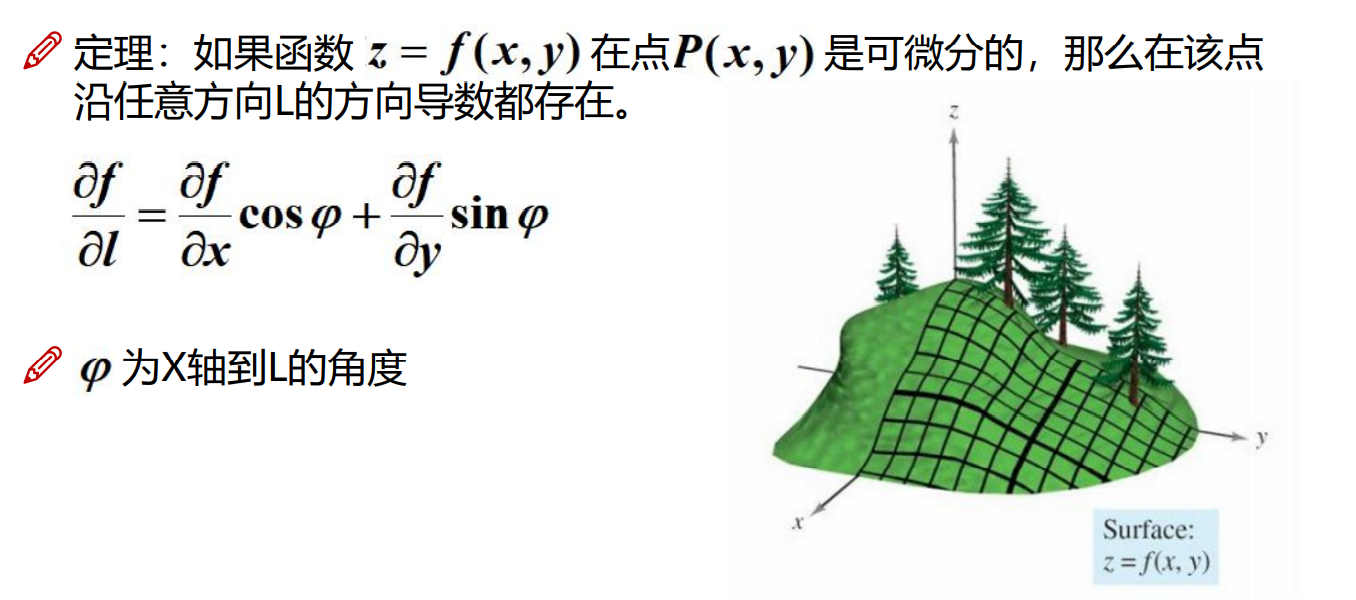
注：主要运用上面那个公式来计算！

1.3梯度的概念

注：gradf 表示梯度！

1.3.1 梯度的习题演示（帮助理解！）

2.拉格朗日乘子法

2.1概念理解

主要理解其为什么可以这样搞！

2.2求解方法

注：类似上面的方程组，解出的值就是答案！

2.3自变量多于两个的情况下的求解

3.矩阵

3.1行列式

3.1.1行列式的计算

二阶行列式的计算↓

三阶行列式的计算↓

3.2矩阵

3.2.1矩阵的概念

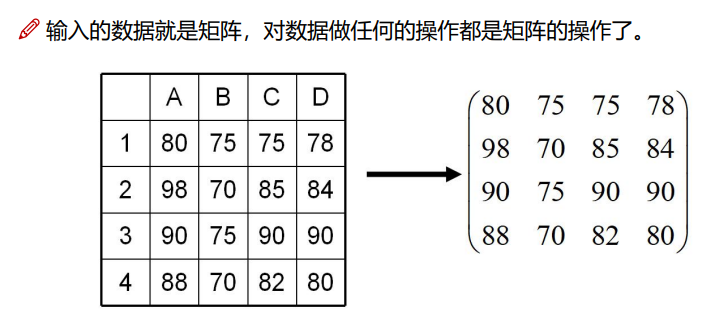
3.2.2矩阵的组成

3.2.3方阵的概念

注：方阵和行列式是两个概念

区别：方阵是n^2个数按一定方式排成的数表，而行列式这是这些数按一定的运算法则所确定的一个数。比如说(O)代表方阵里的所有元素均为0，而行列式仅代表值为0。

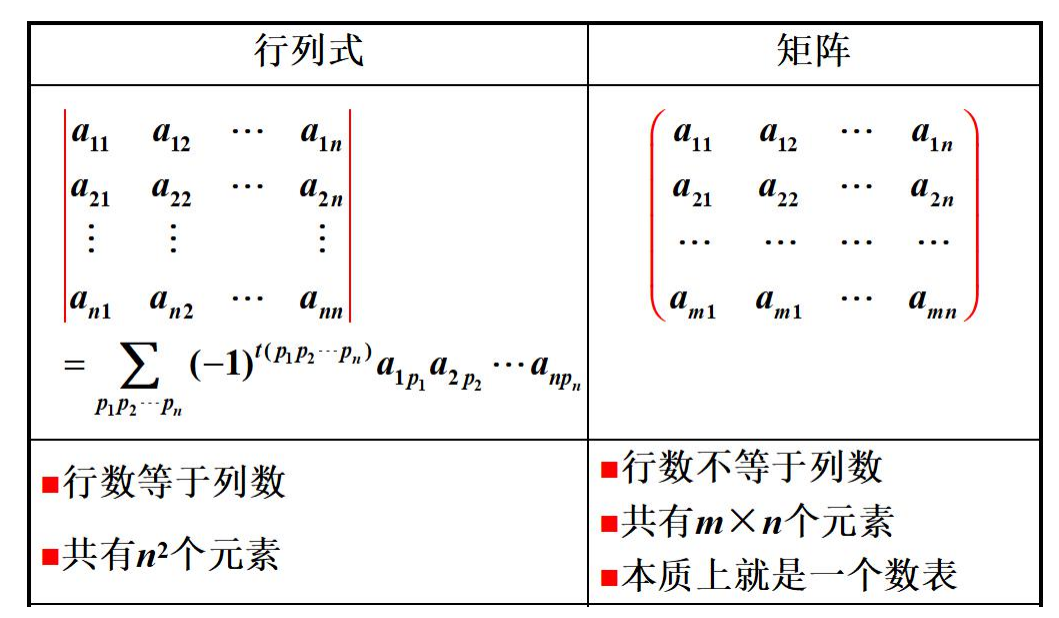
3.2.4行列式和矩阵的区别

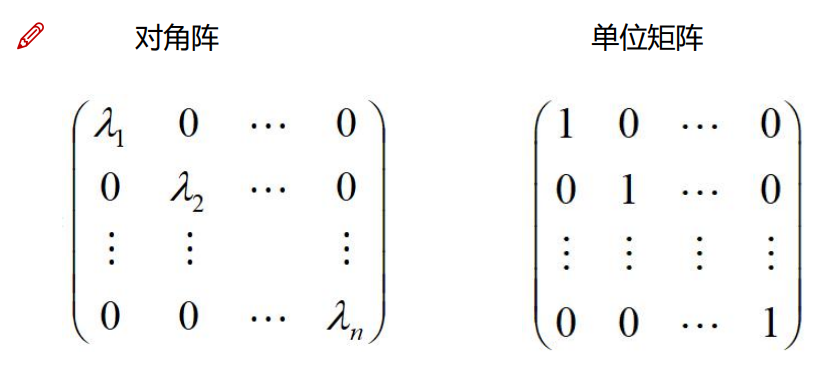
3.2.4几个特殊的矩阵

上三角矩阵和下三角矩阵

对角阵和单位矩阵

3.3矩阵的基本运算

3.3.1 矩阵的加减法

数乘运算

3.3.2矩阵的乘法

3.3.3 矩阵乘法的一些基本法则

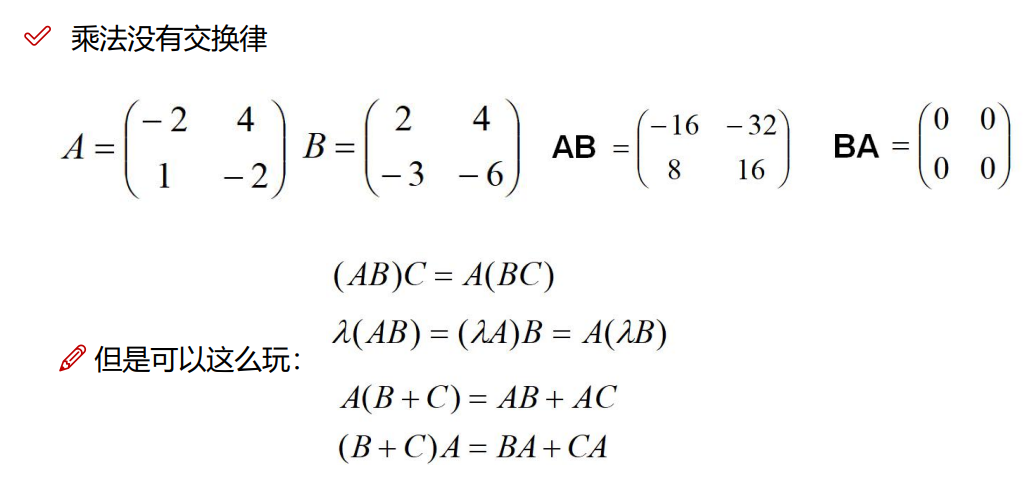
3.3.4 未知矩阵的求解

3.3.5 矩阵倒置

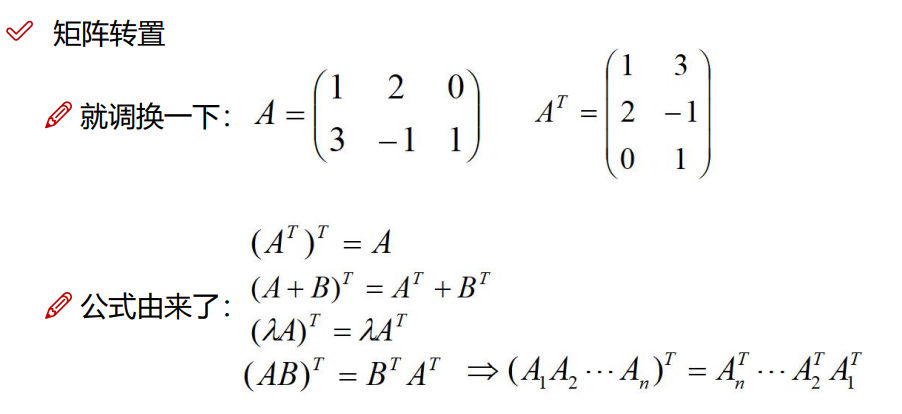
3.3.6 对称矩阵

3.3.7 逆矩阵

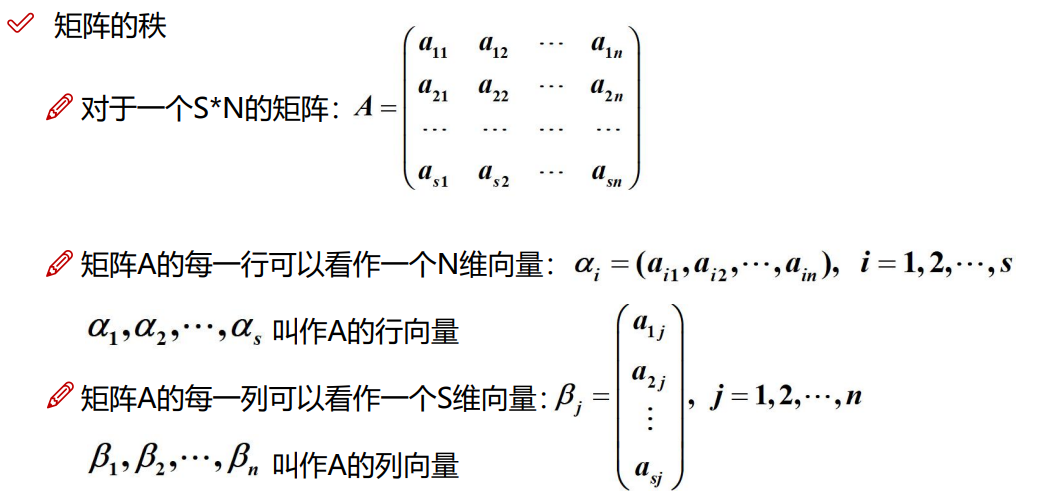
3.4 矩阵的秩

注：秩的存在减少了冗余，一个矩阵A的列秩是A的线性无关的纵列的极大数。

3.5 其他

3.5.1向量的内积

3.5.2 向量的长度

3.5.3 向量的正交

注：向量的正交说白了就是相互垂直！

3.5.4 规范正交基

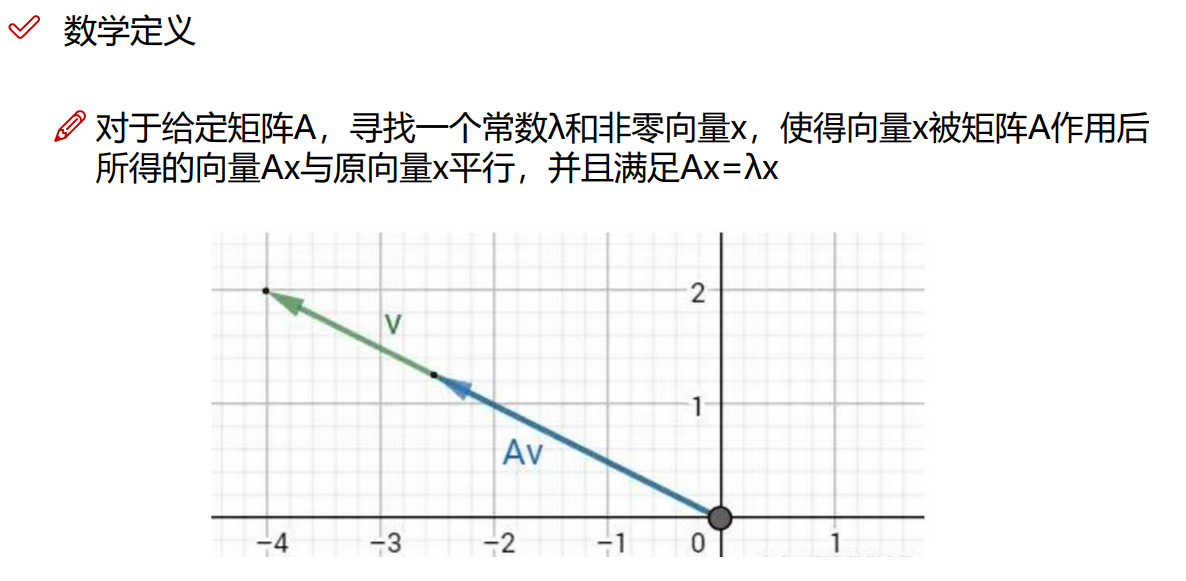
4.特征值和特征向量

4.1 基本概念

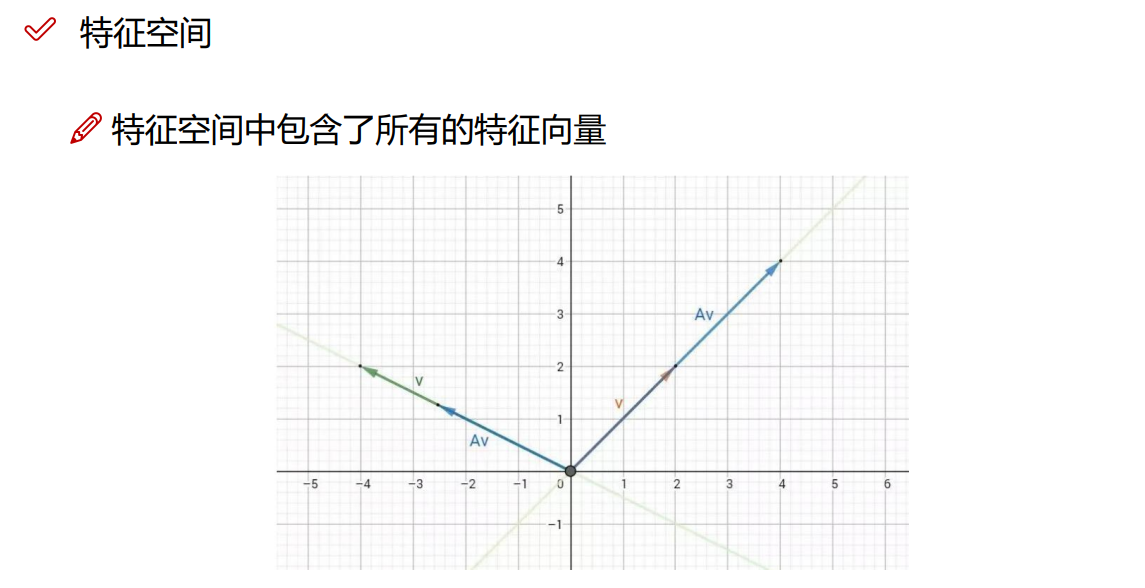
4.2 SVD

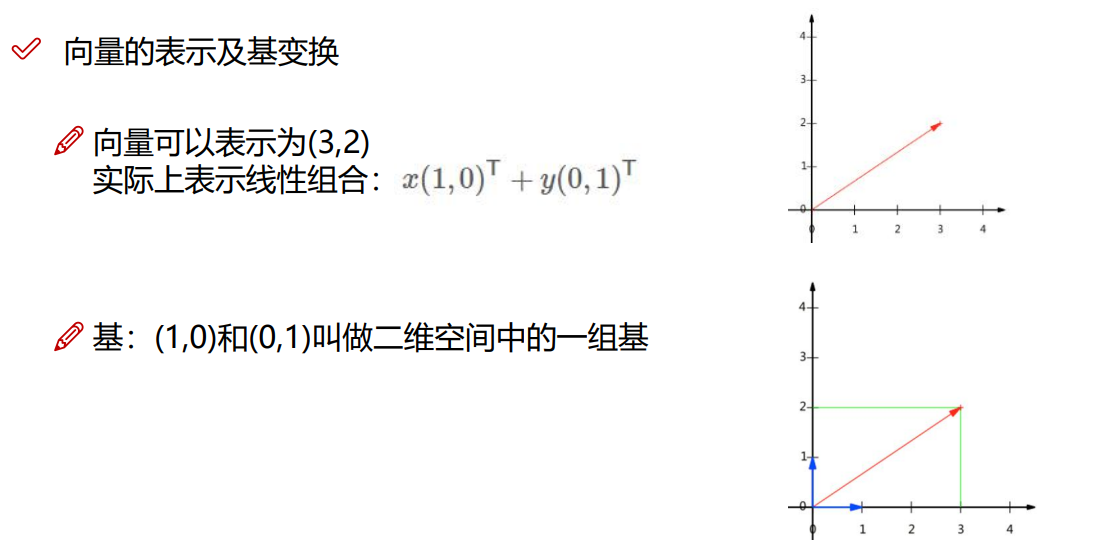
4.2.1 向量的表示

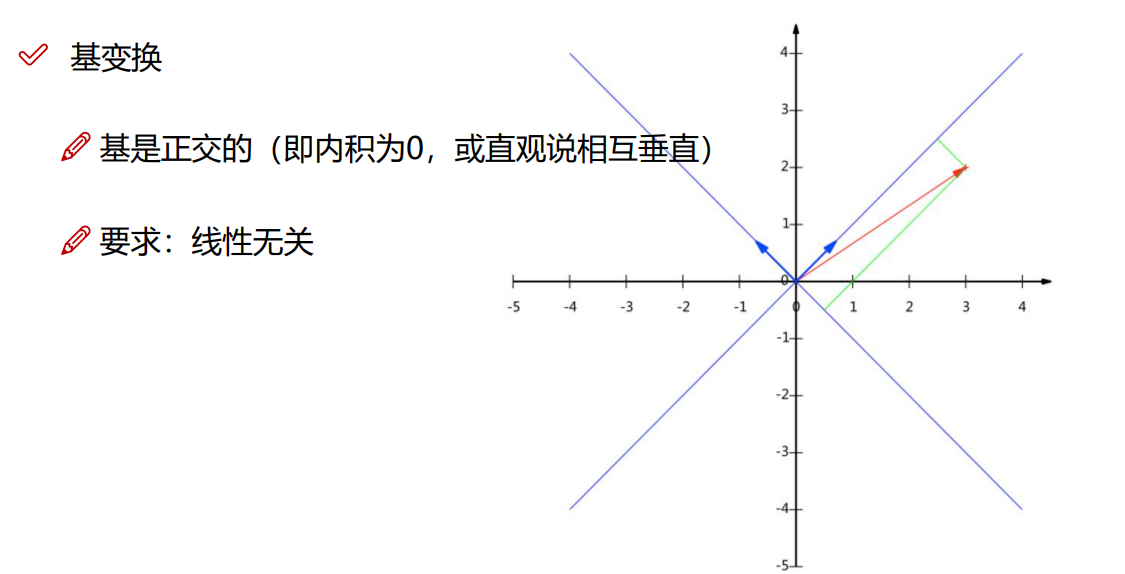
4.2.2 基变换

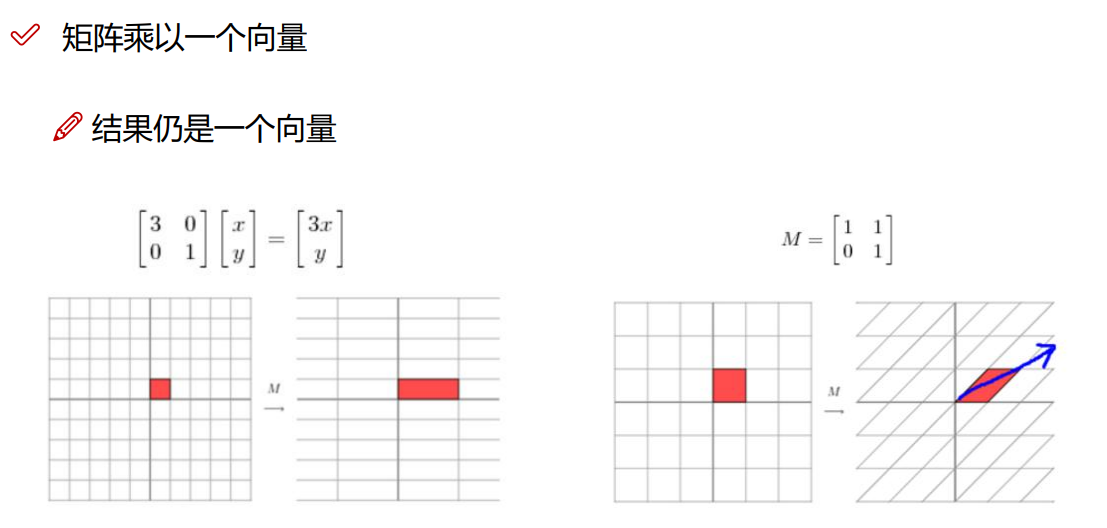
4.2.3 矩阵乘以一个向量

4.2.4 特征值分解

4.2.5 SVD推导

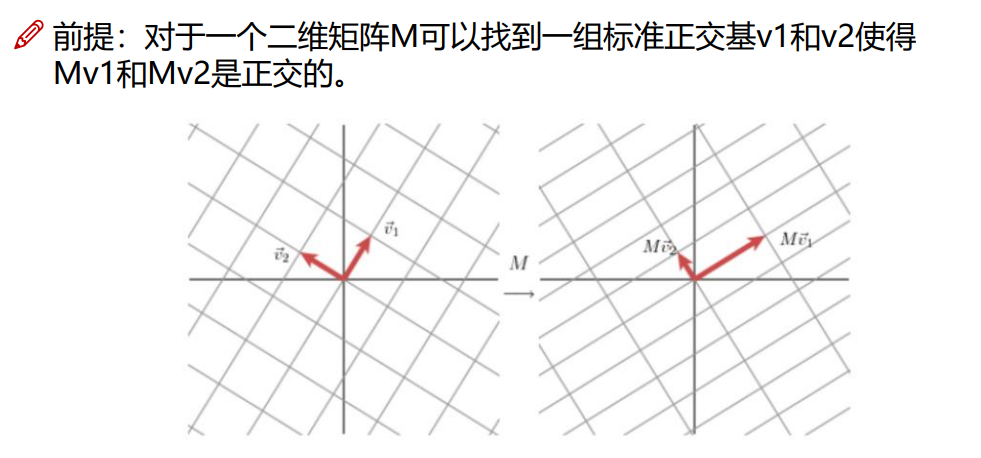
5.随机变量

5.1 概率密度函数

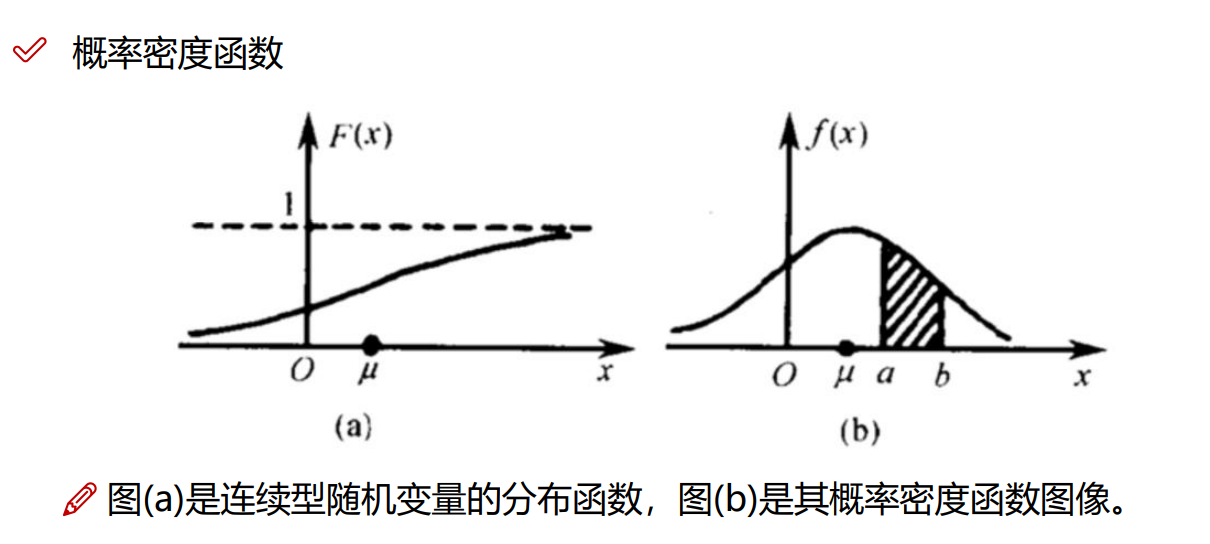
注：说白了就是导数

5.2 简单随机抽样

5.3 似然函数

5.4 极大似然估计

5.4.1 极大似然估计求解

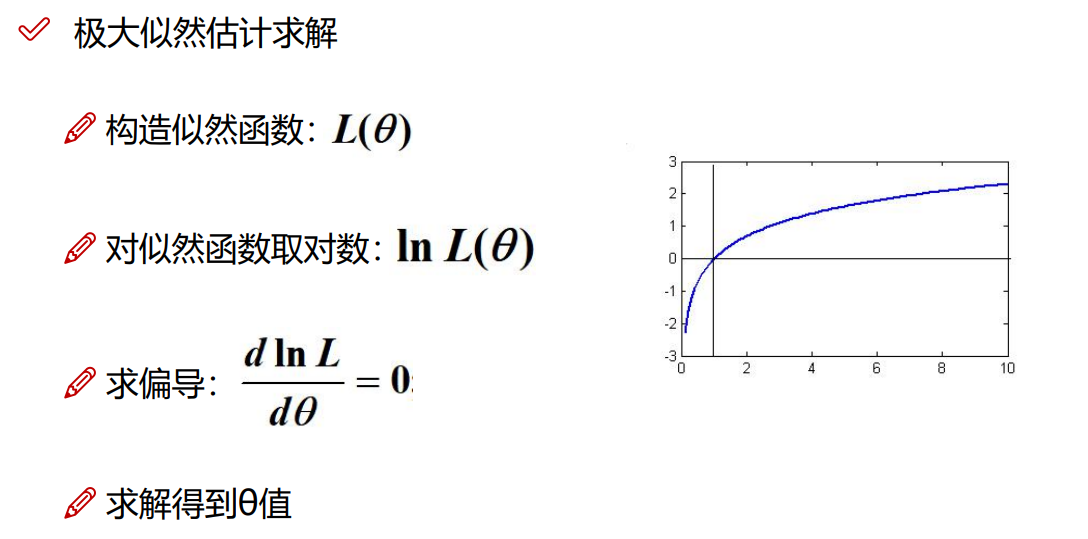
注：求的是极值点，不是值！！！

例子

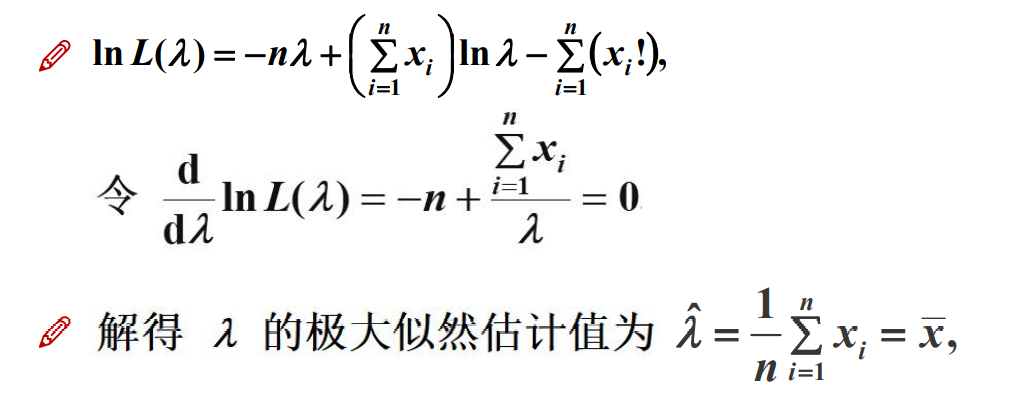
6.概率论

6.1 频率与概率

注：频率是在一次试验中某一事件出现的次数与试验总数的比值；

​ 概率是某一事件所固有的性质.

6.2 条件概率

6.3 独立性

6.4 独立实验

6.5 二维随机变量

6.5.1 二维随机变量的性质

6.5.2 二维随机变量的概率分布

例子：

6.5.3 二维连续型随机变量

例子：

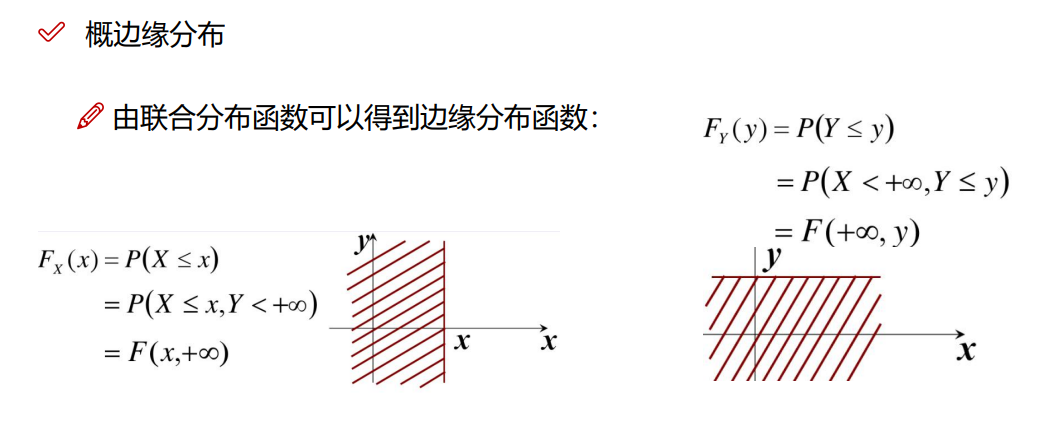
6.6 边缘分布

6.7 期望（二维情况）

例子：

6.7.1 期望的性质

6.8 方差

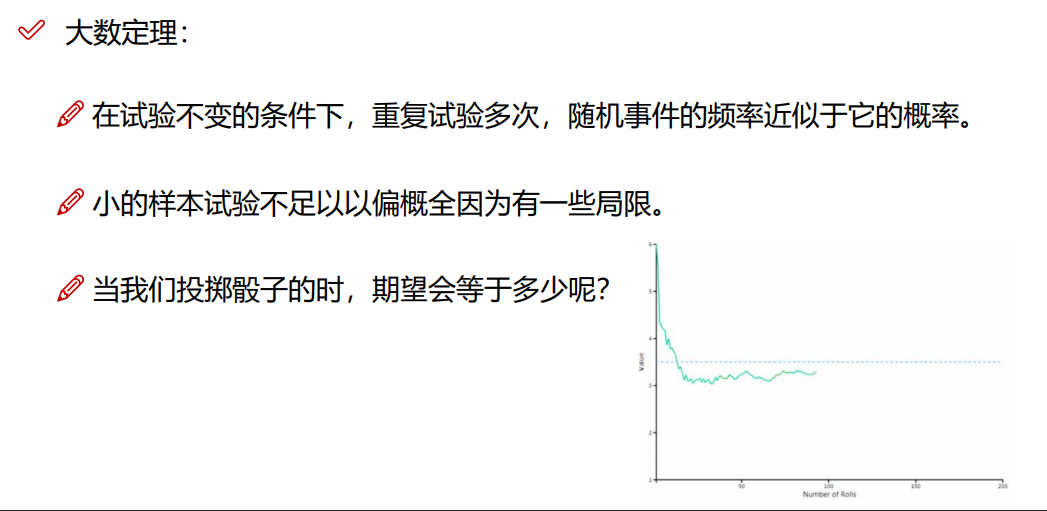
补充：大数定理

6.9 补充

6.9.1 马尔科夫不等式

6.9.2 切比雪夫不等式

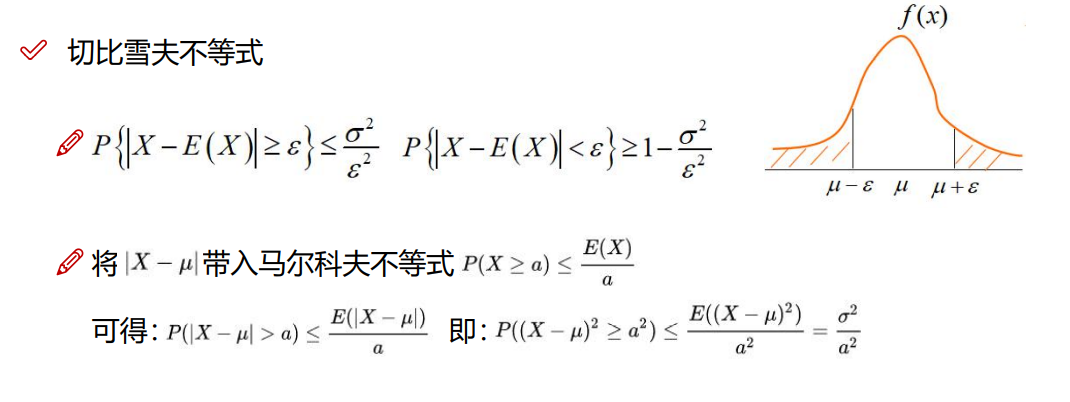
例子：

6.9.3 中心极限定理

网址：Sampling Distributions (onlinestatbook.com)

6.10 后验概率估计

最大后验概率与最大似然估计区别

7.几种分布(更多的看.ipynb详细代码)

7.1 正态分布

7.2 二项式分布

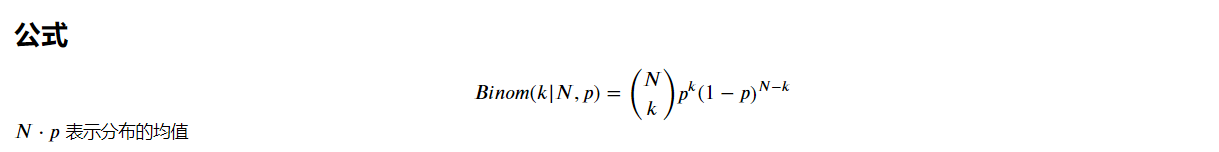
7.3 泊松分布

例子：

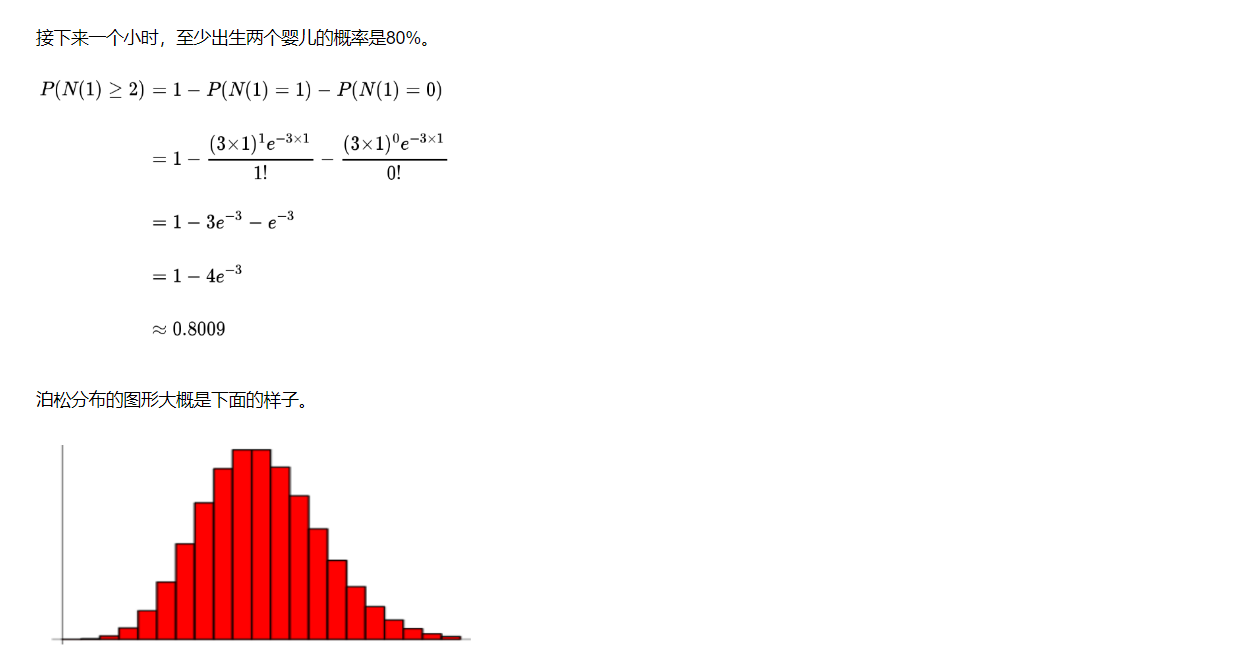
7.4 均匀分布

7.5 卡方分布

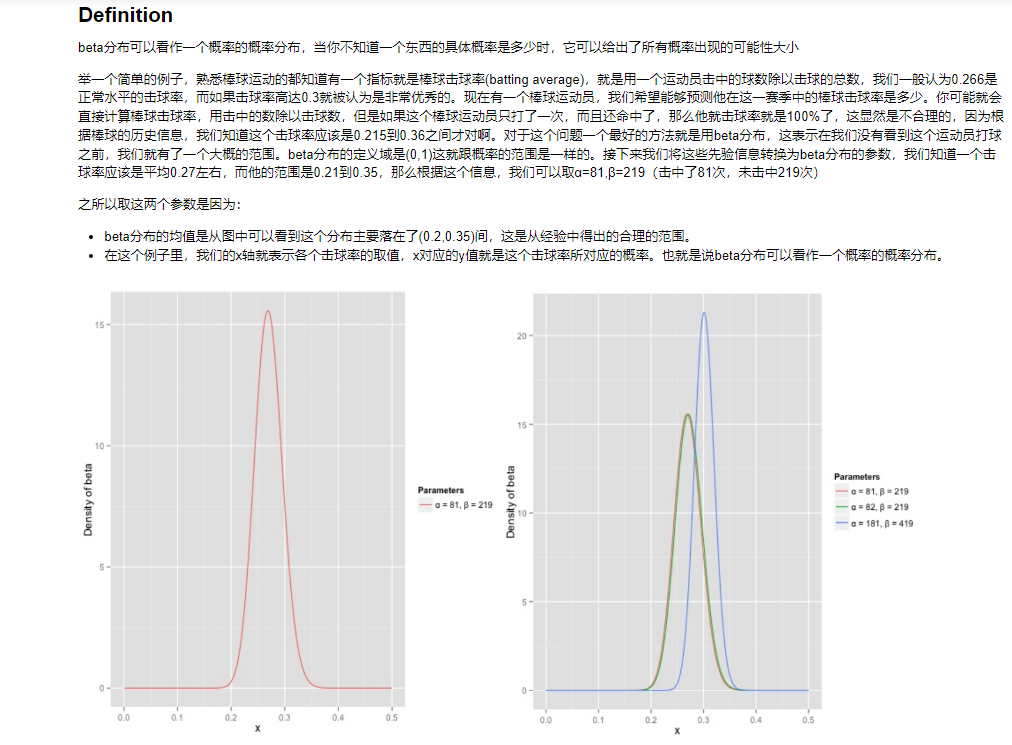
7.6 Beta分布

8.核函数

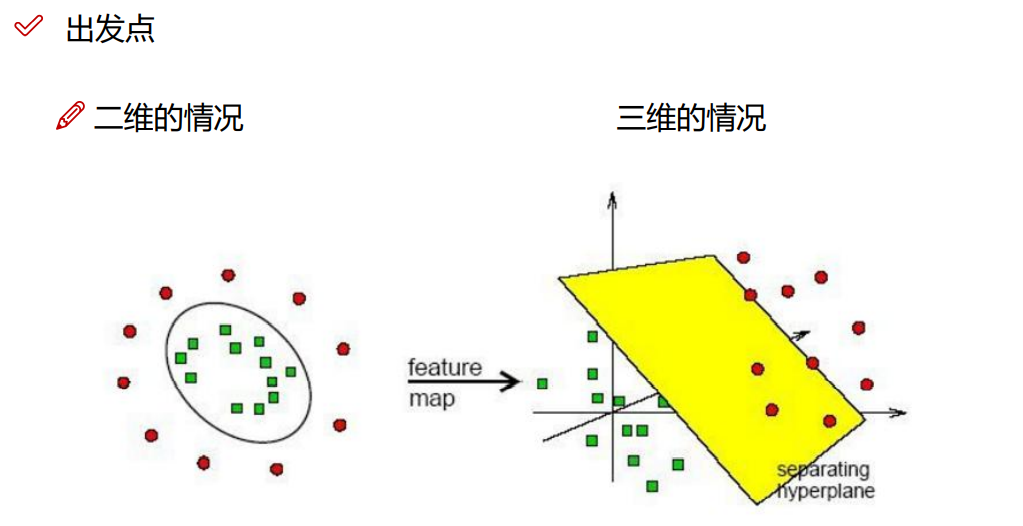
8.1 线性核函数

8.2 多项式核函数

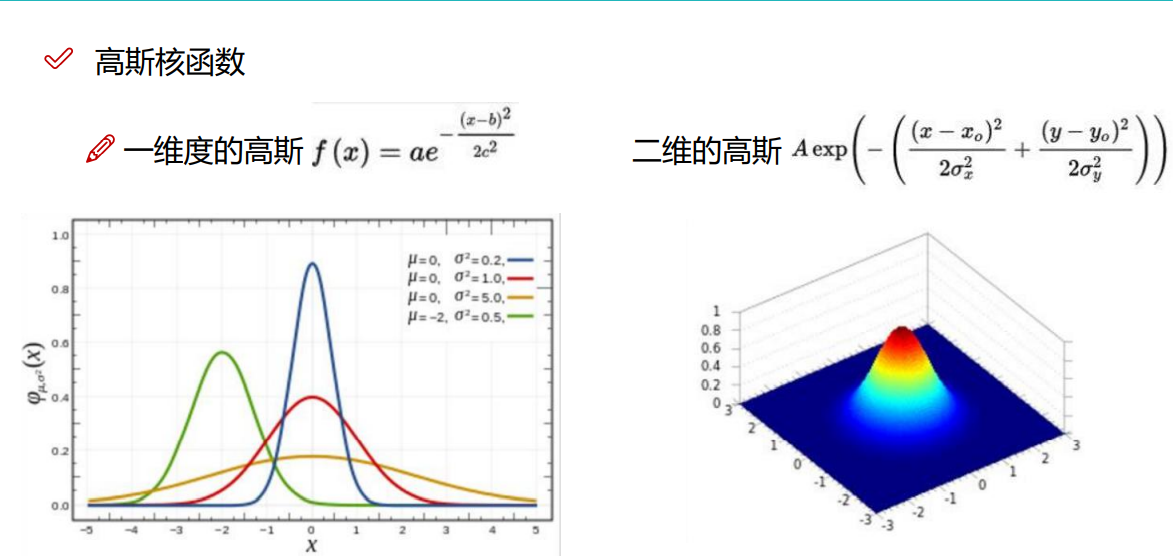
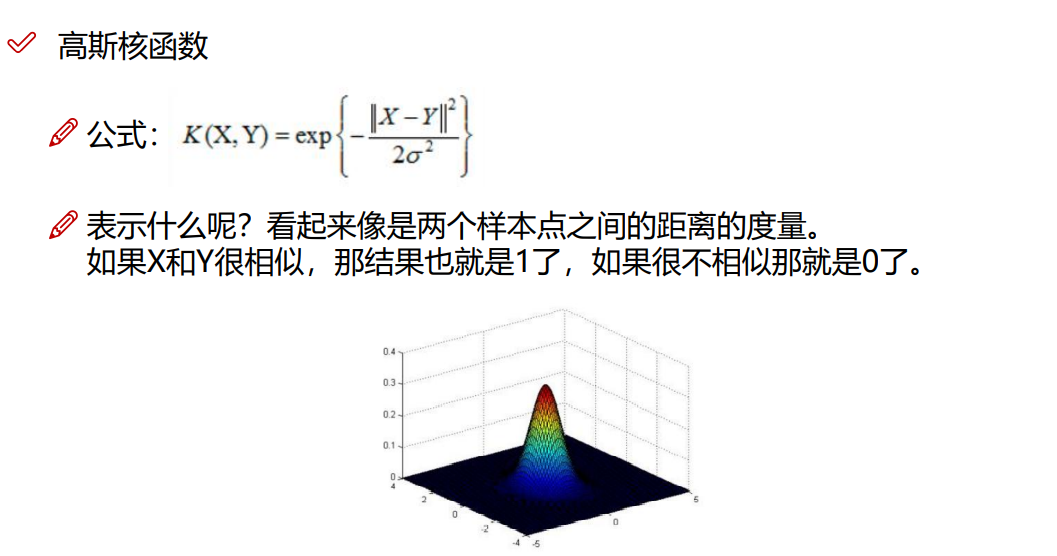
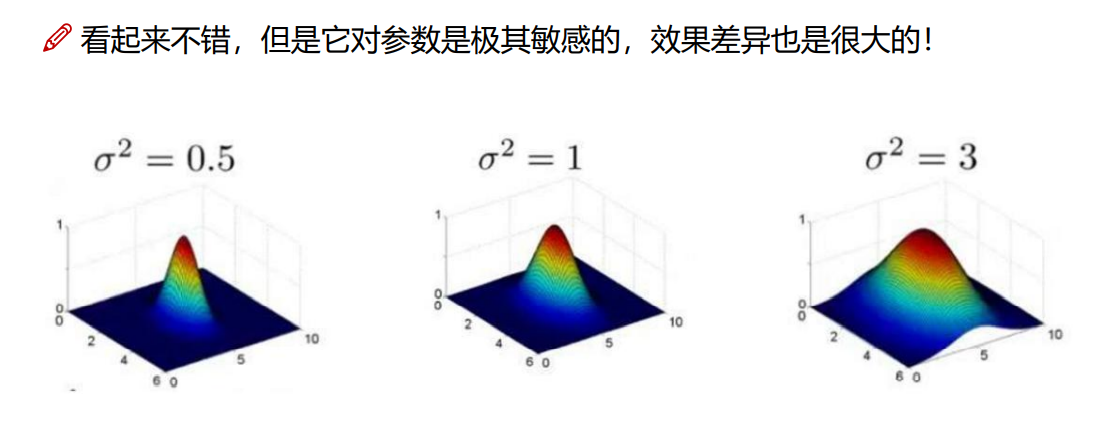
8.3 高斯核函数（最常用）

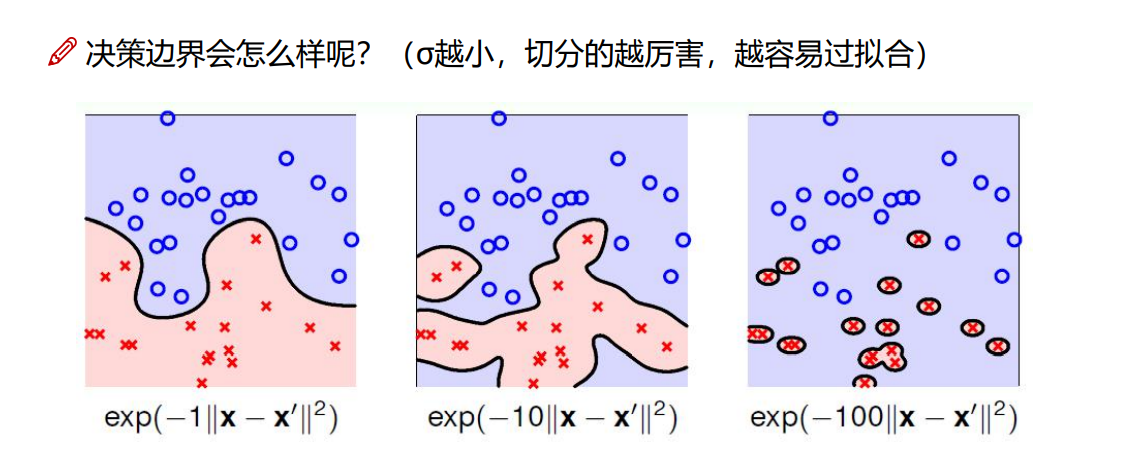
9.熵和激活函数

9.1 熵

9.2 激活函数

9.2.1 常见激活函数

Sigmoid函数

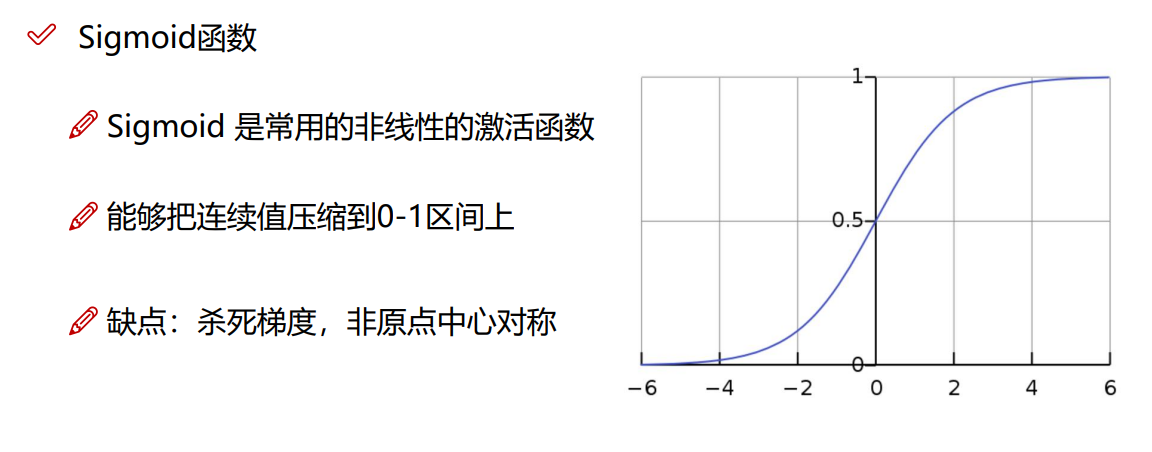
问题：

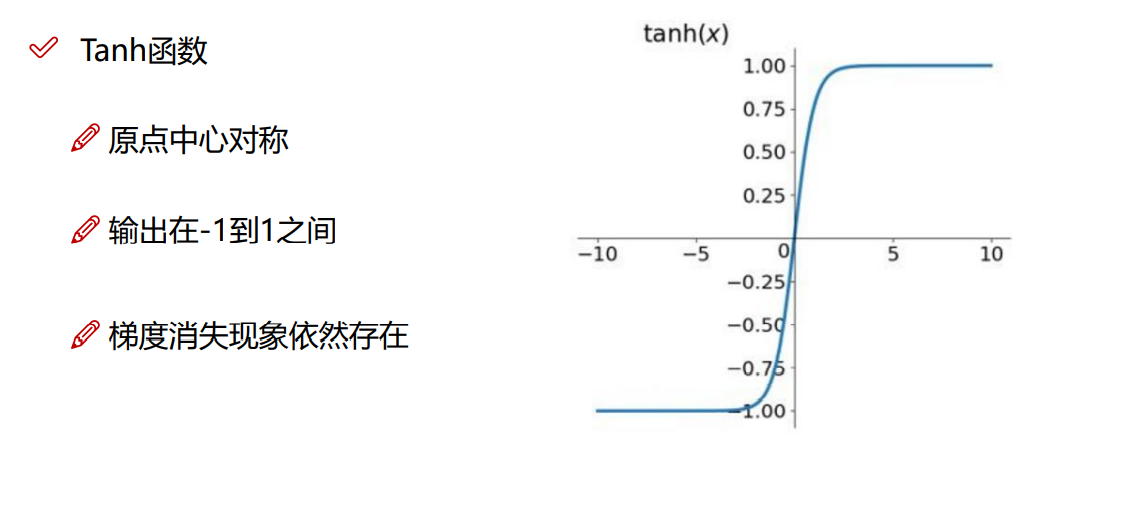
Tanh函数

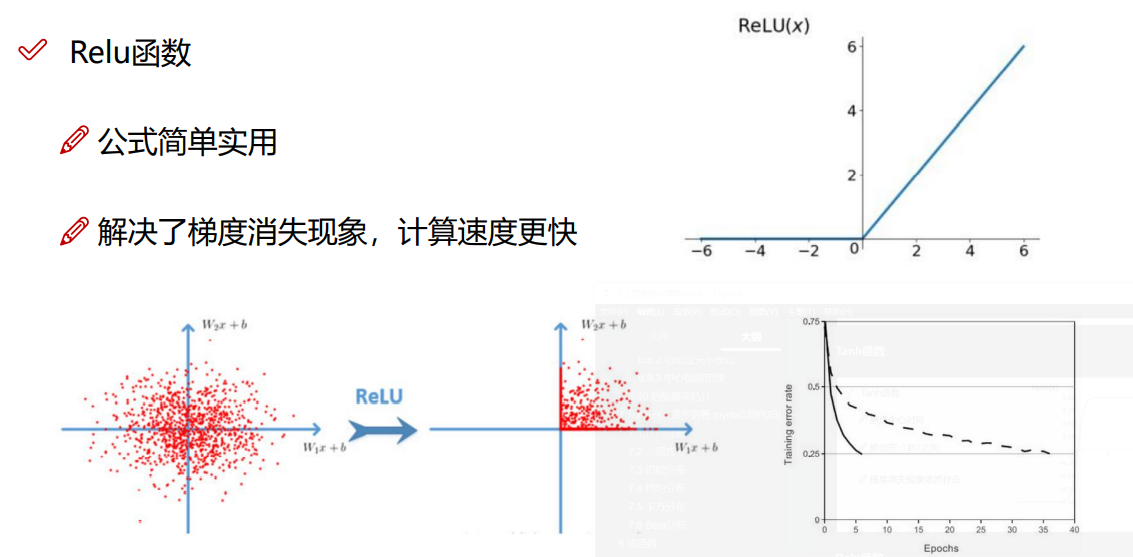
R e l u 函数

更好的版本：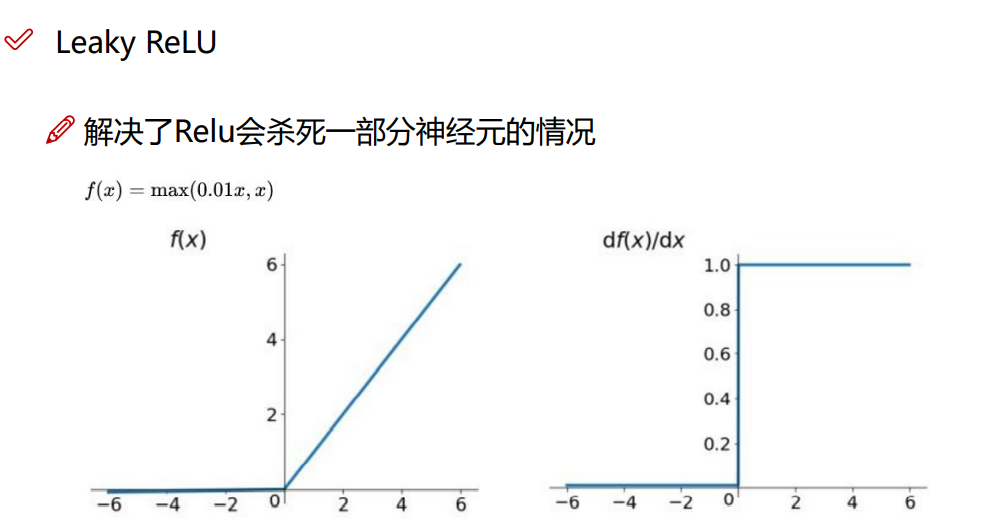

10.回归分析

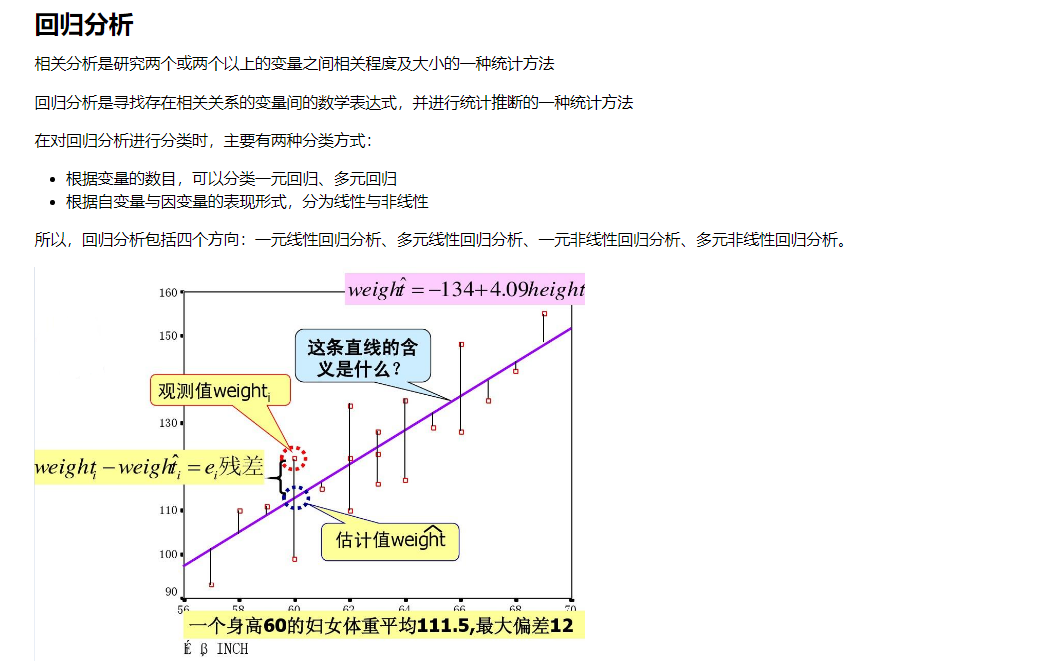
10.1 一元线性回归

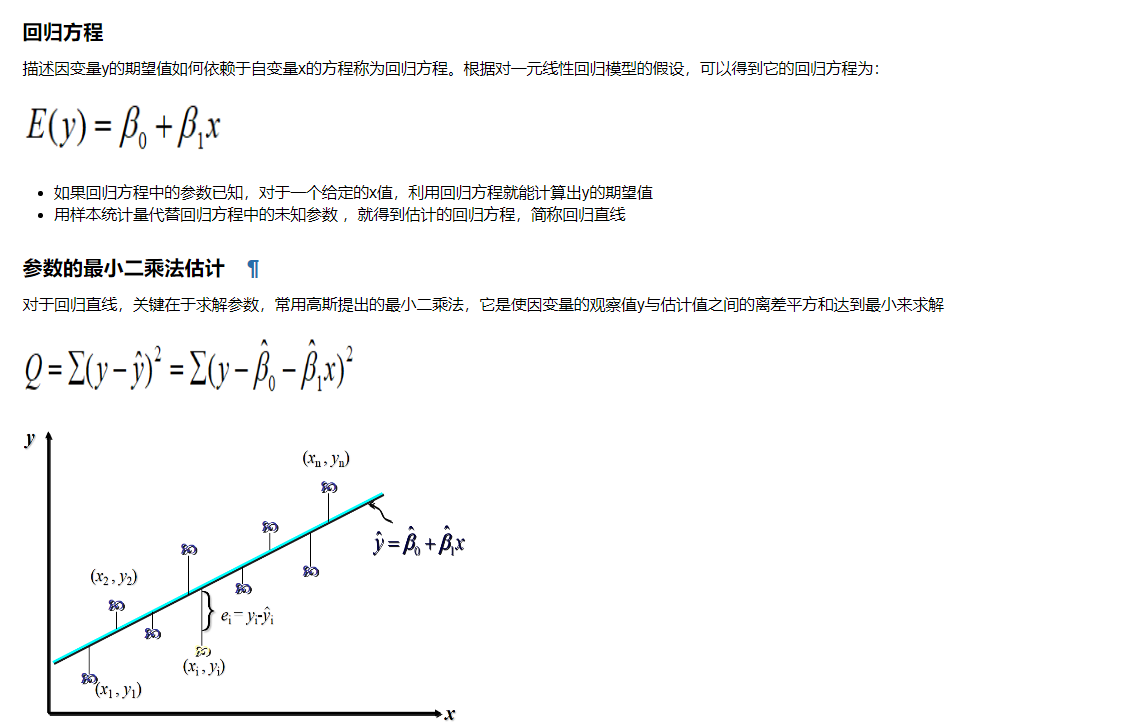
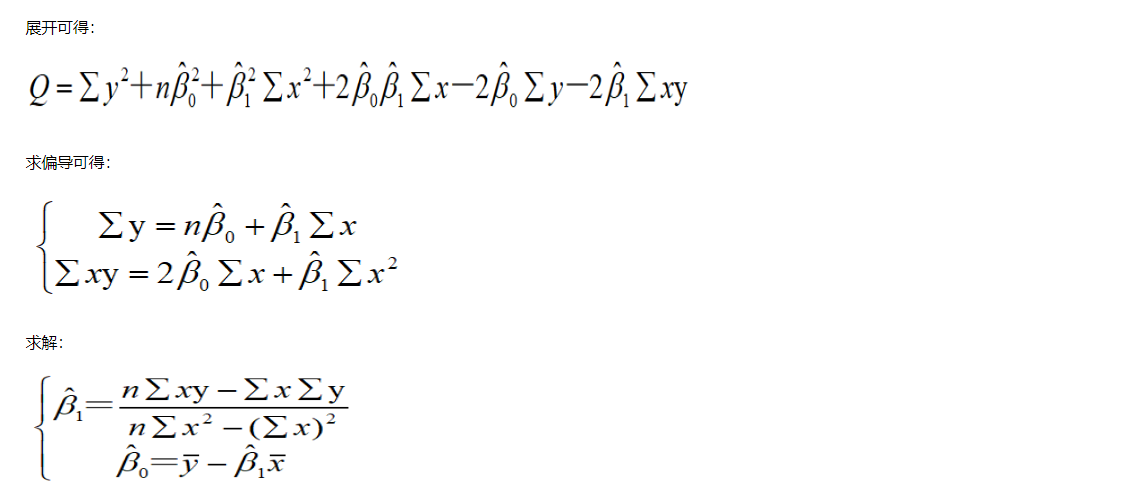
实例：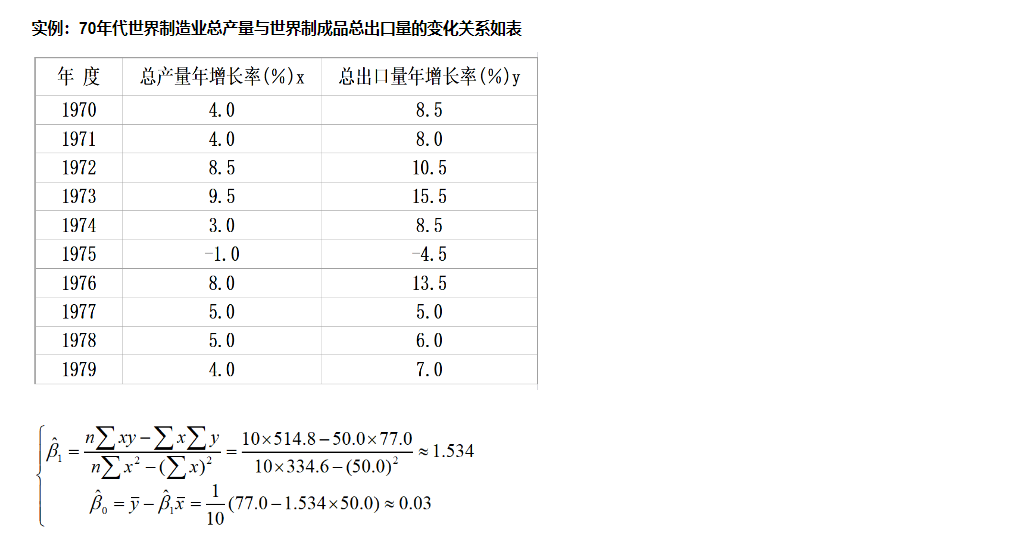

10.1.1 标准差计算

10.1.2 置信区间估计

实例：

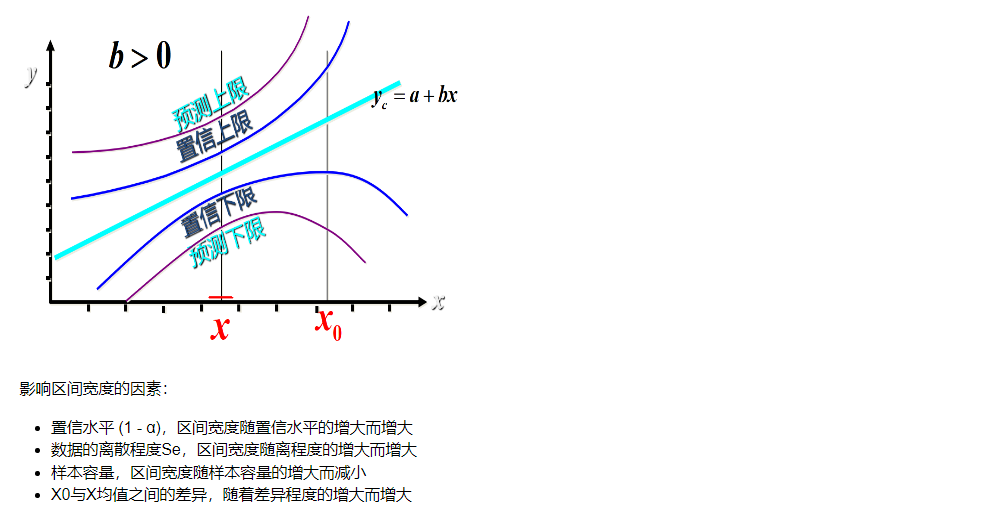
10.1.3 回归直线的拟合优度

10.1.4 判定系数

10.1.5 显著性检验

10.1.6 线性关系检验

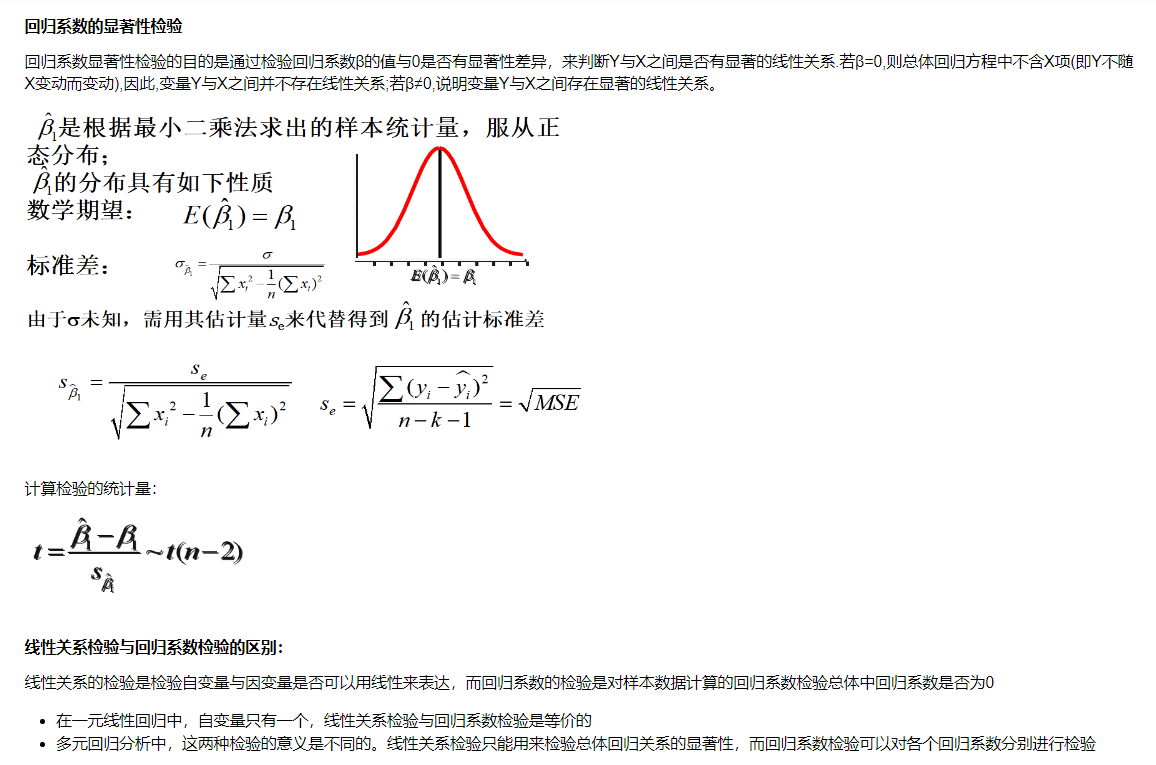
10.2 多元线性回归

10.3 曲线回归

10.4 多重共线性

11.假设检验

11.1 假设检验的基本思想

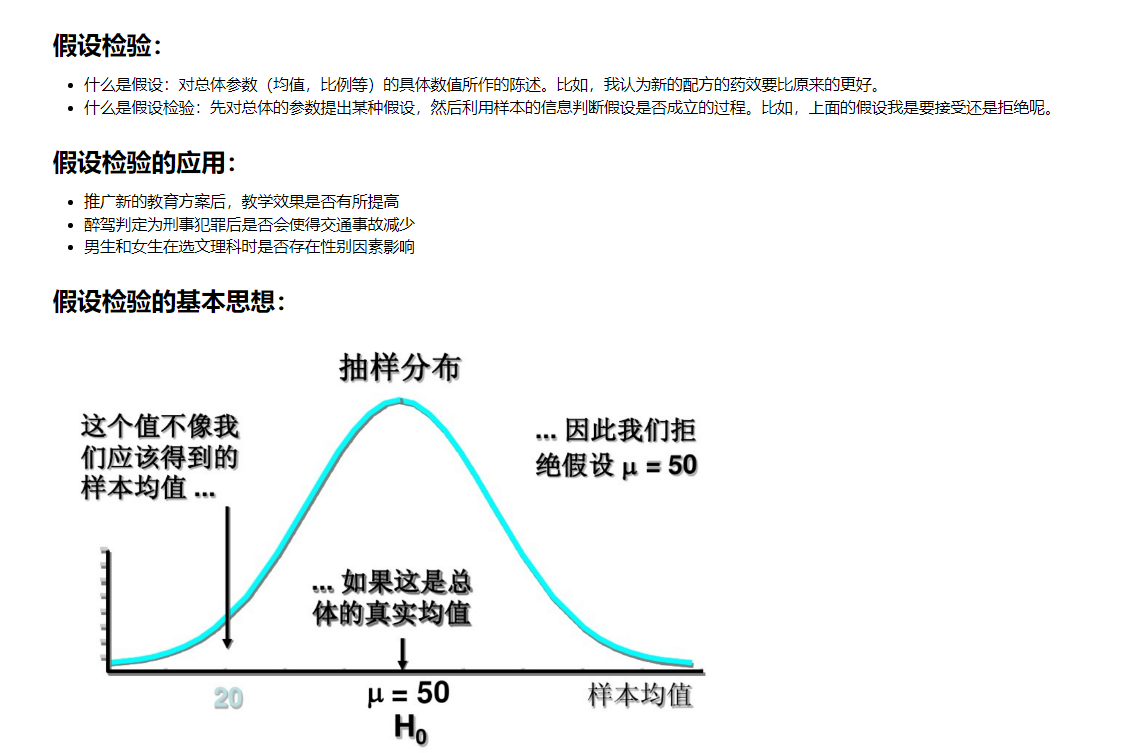
11.2 假设检验的基本概念

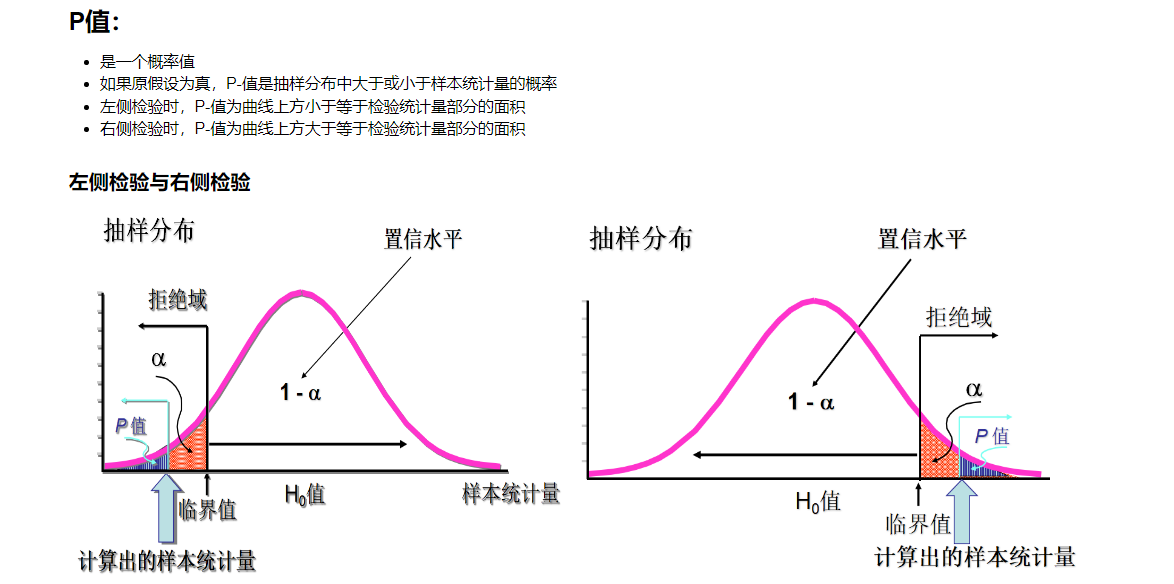
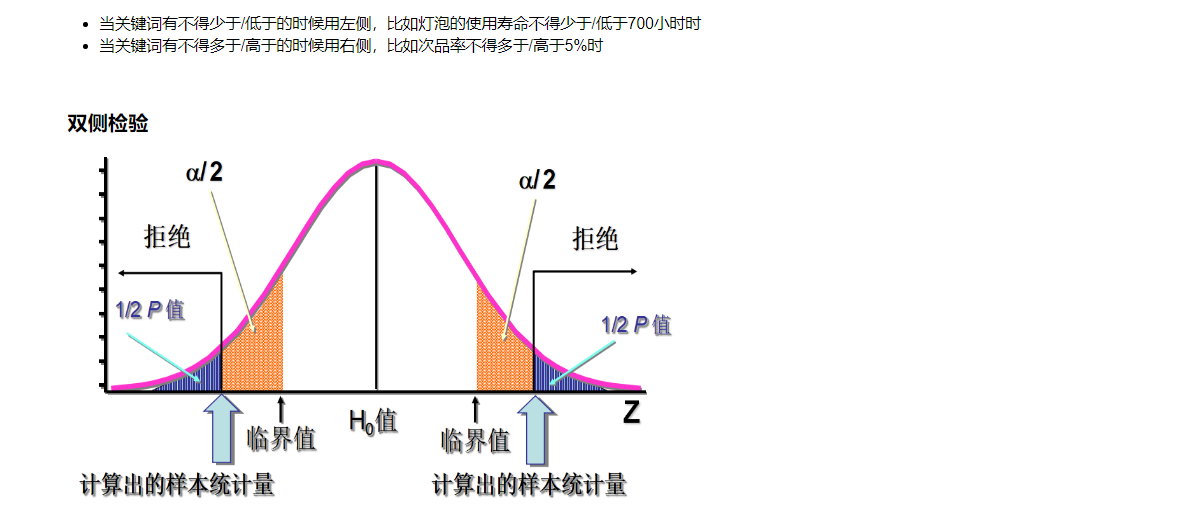
11.3 总体均值检验

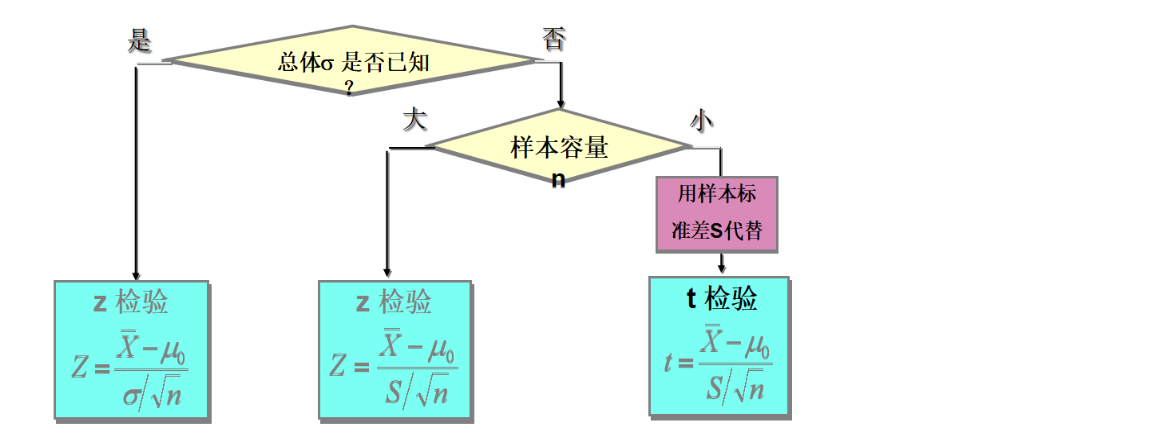
11.3.1 Z检验

公式

原理

实例

11.3.2 T检验

注：临界值表>>>http://www.docin.com/p-1173562569.html

实例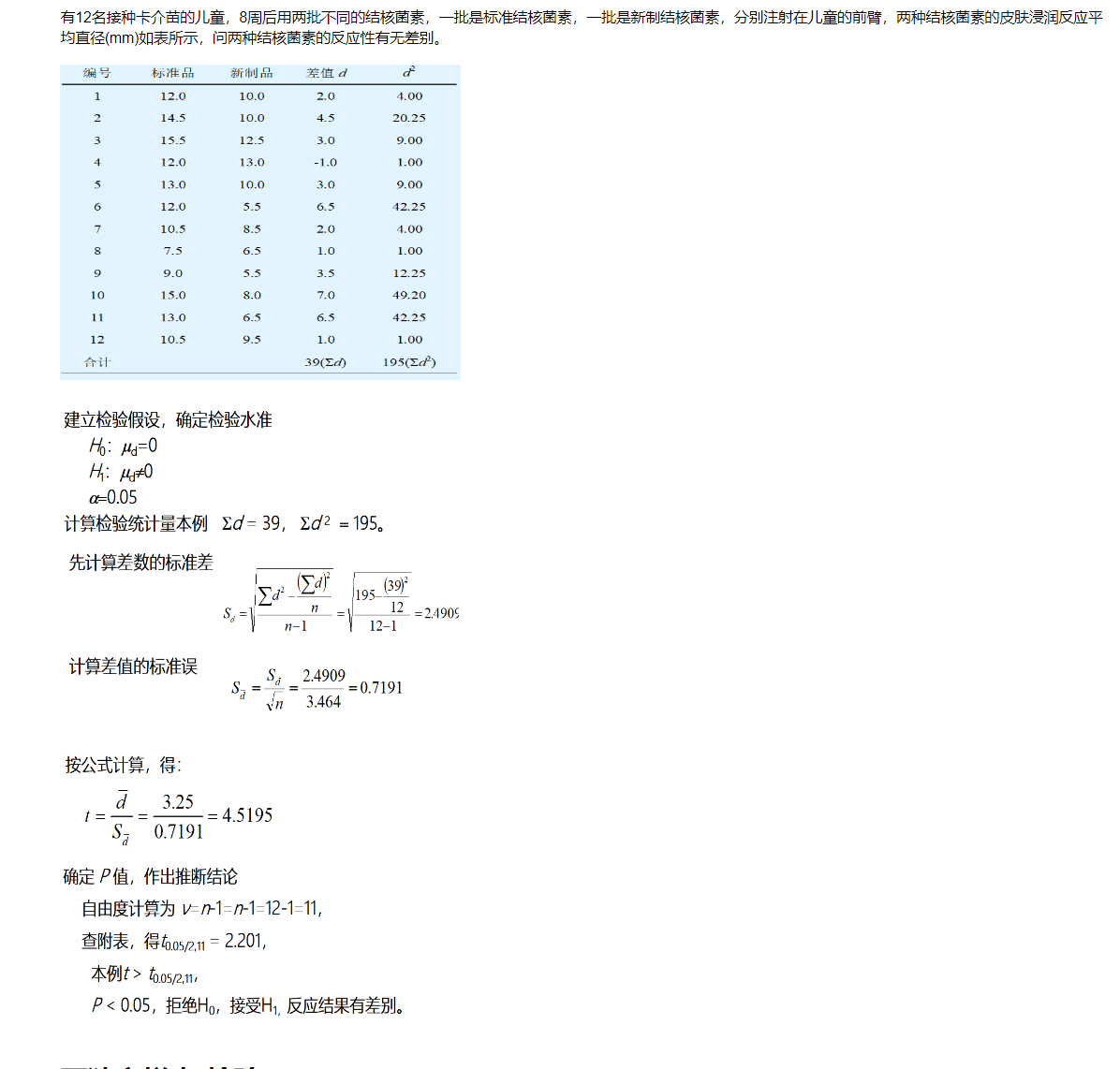

实例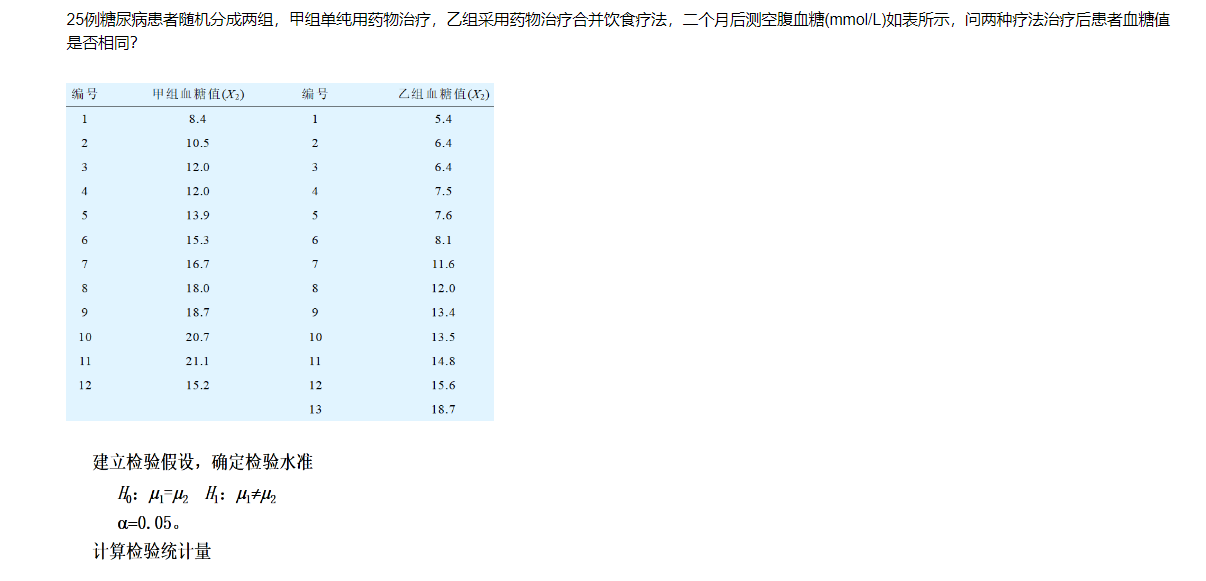

11.3.3 正态性检验和两总体方差的齐性检验

实例

11.4 卡方检验

实例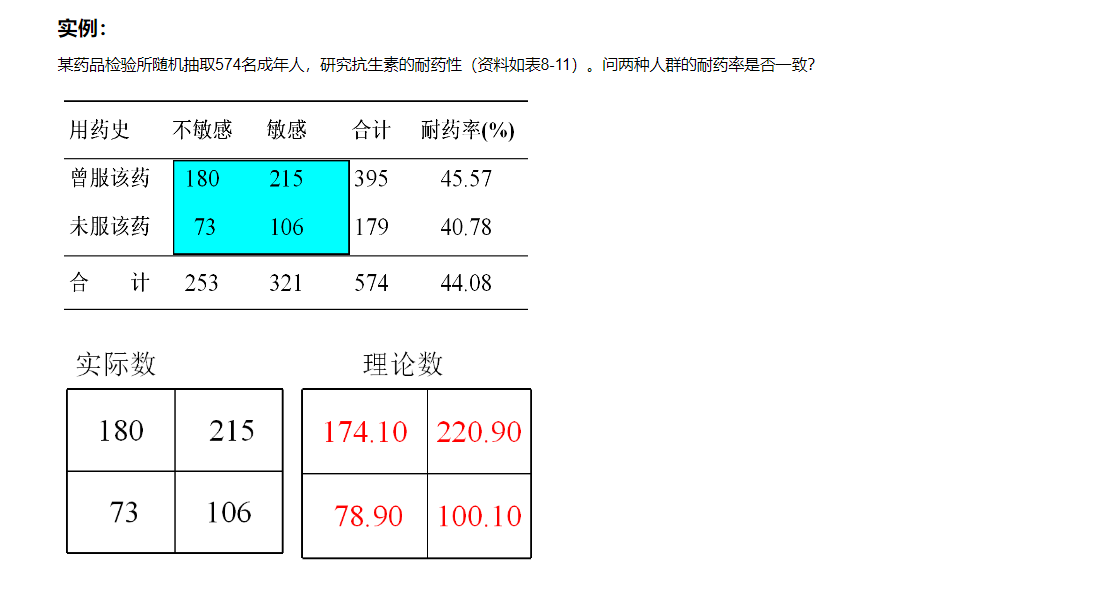

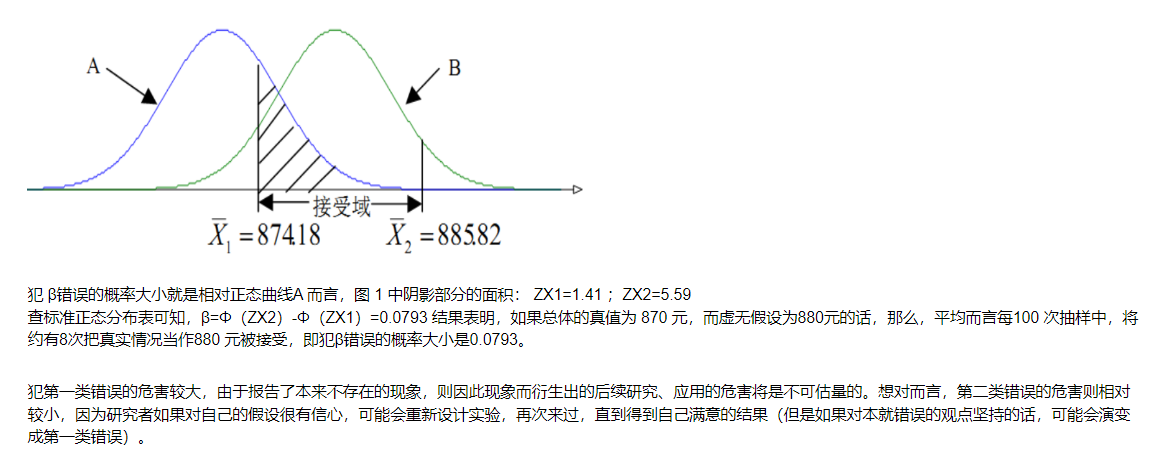
11.5 假设检验中的两类错误

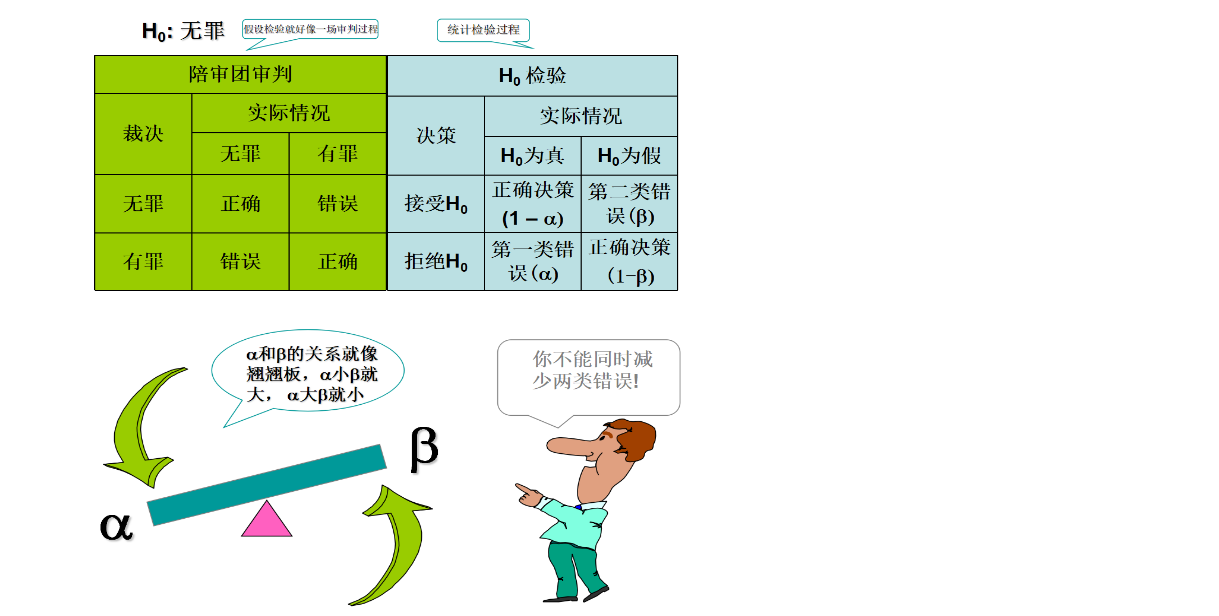
实例

12.相关分析

12.1 基本概念

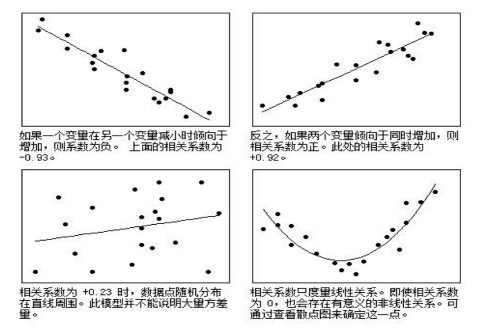
12.2 连续变量的相关分析

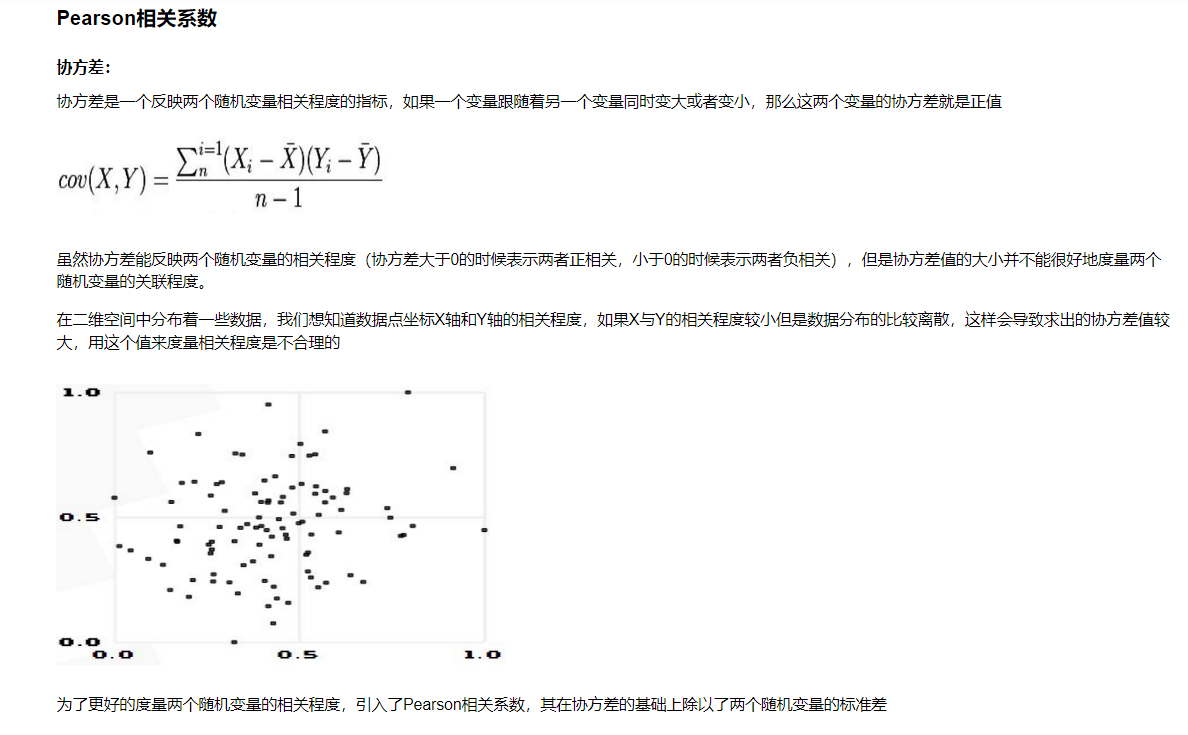
12.3 相关系数的显著性检验

12.4 等级变量的相关分析

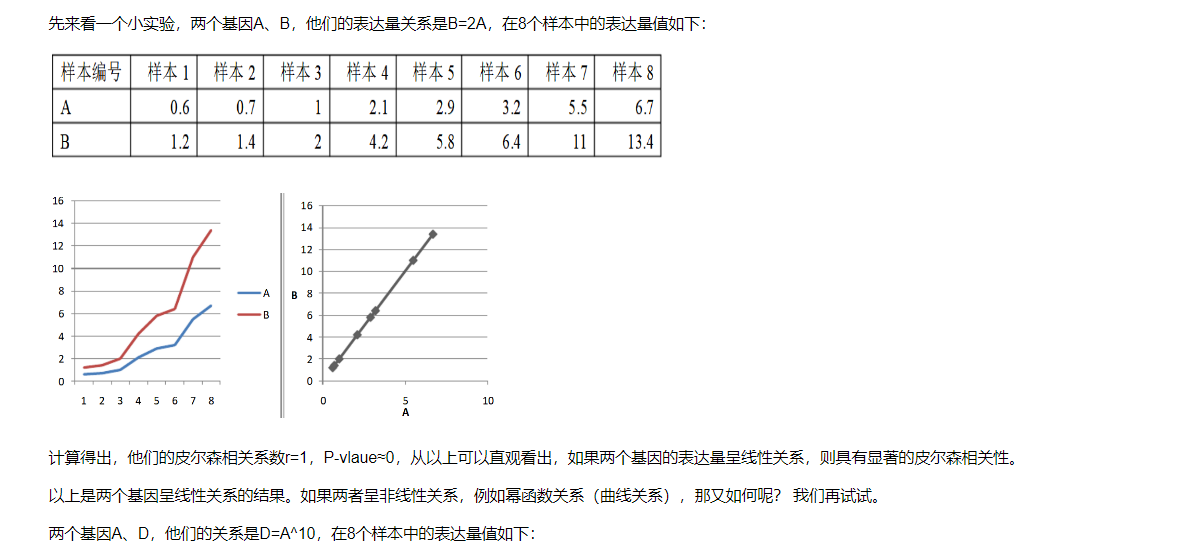
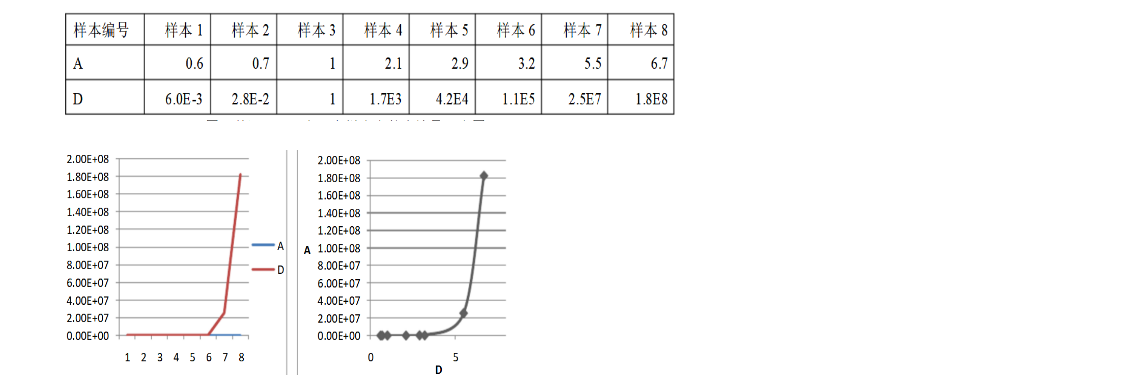
12.4.1 斯皮尔曼等级相关

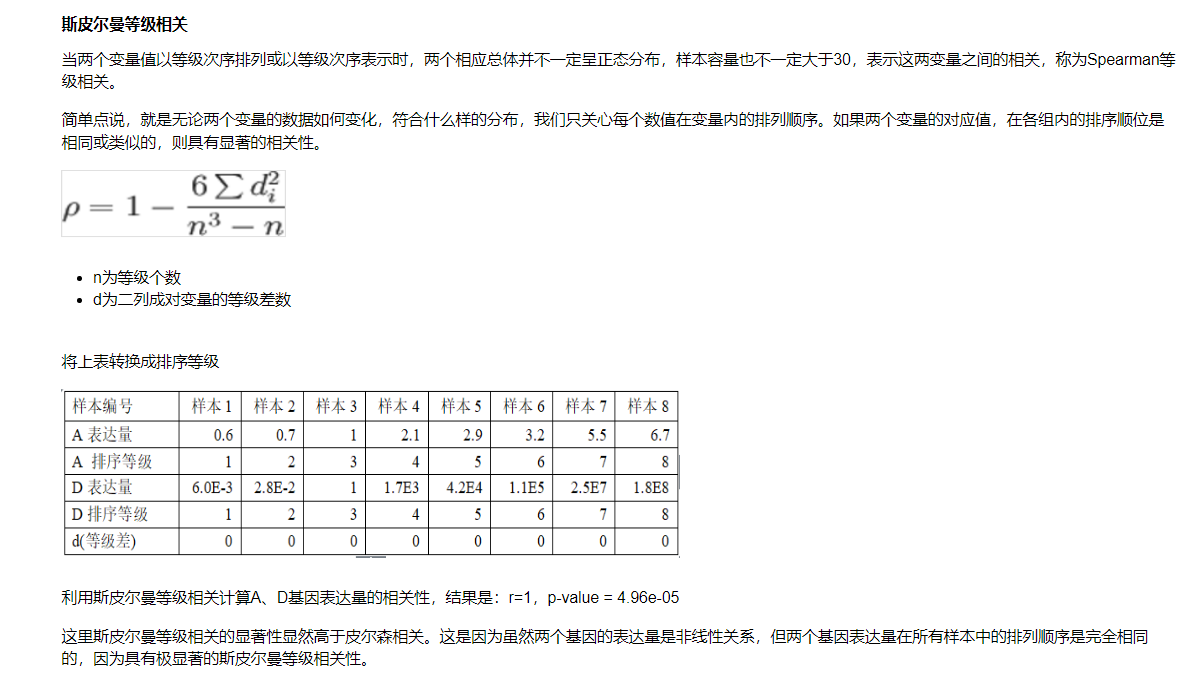
实例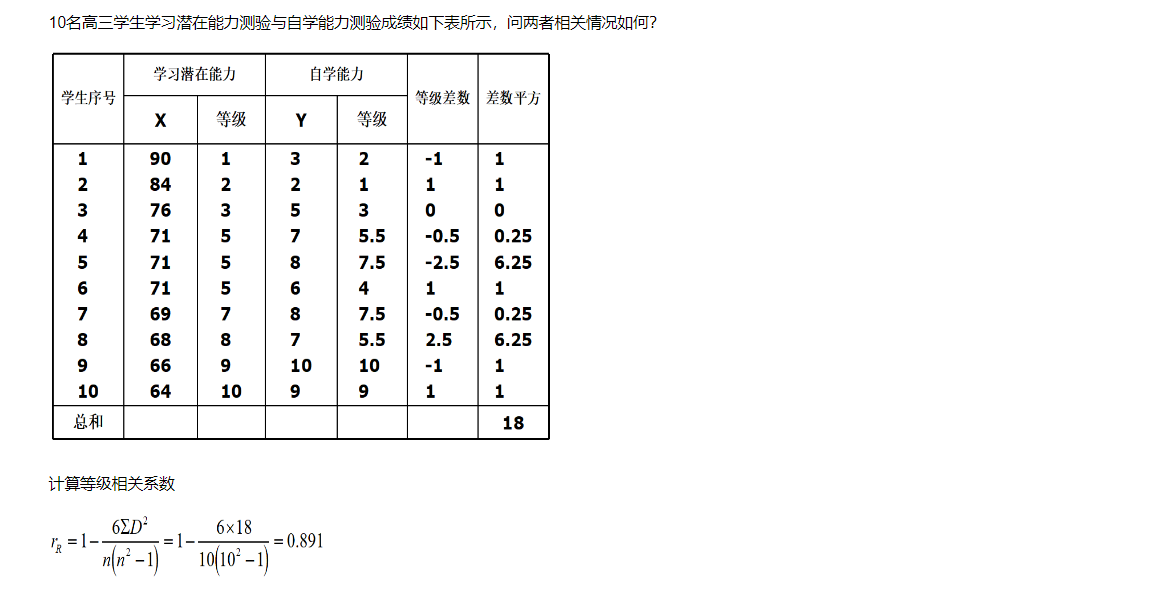

等级相关系数的显著性检验

12.5 肯德尔和谐系数(Kendall)

实例

肯德尔和谐系数的显著性检验

肯德尔和谐系数(W)显著性临界值表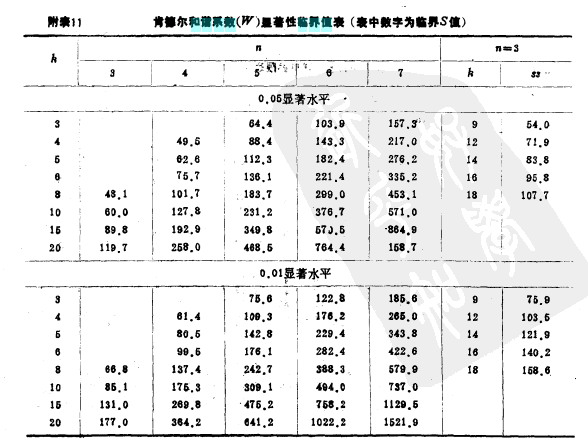

12.6 质量相关分析

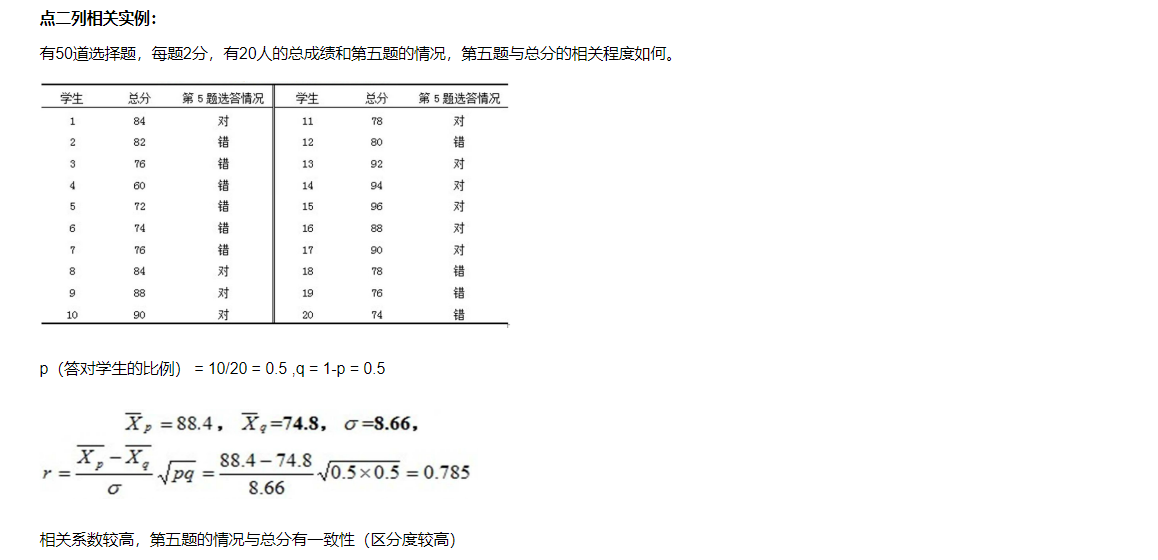
12.7 品质相关分析

φ相关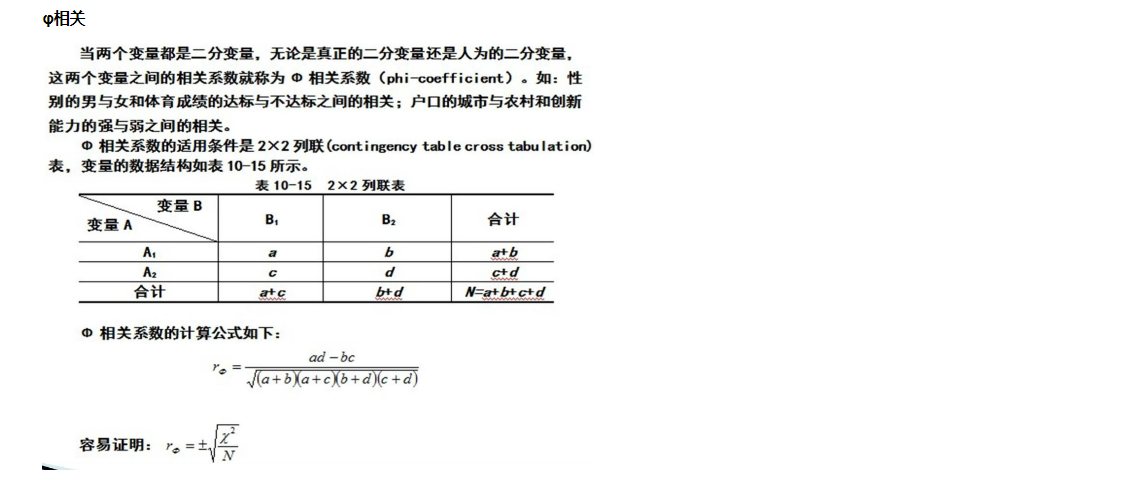

φ相关实例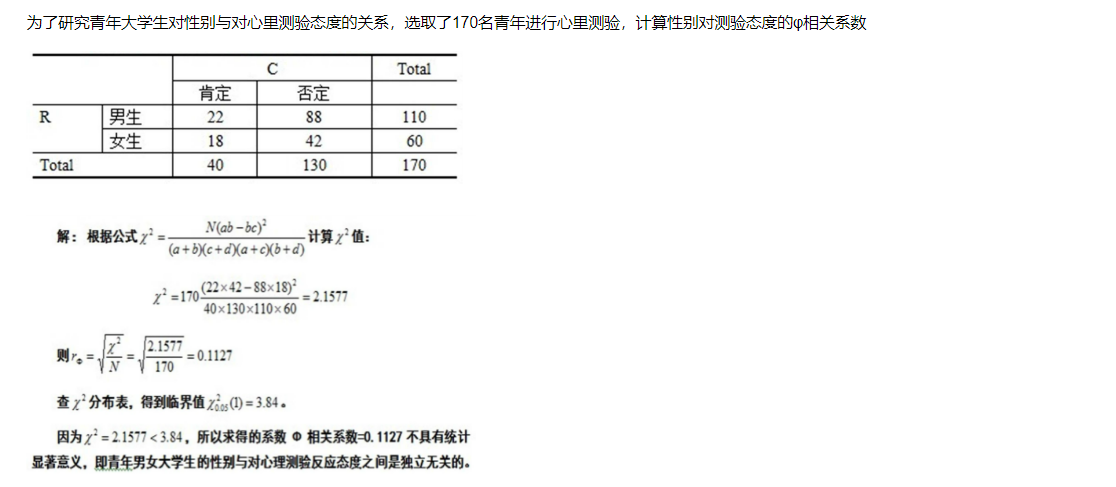

12.8 偏相关分析

12.9 复相关系数

13.聚类分析

13.1 层次聚类

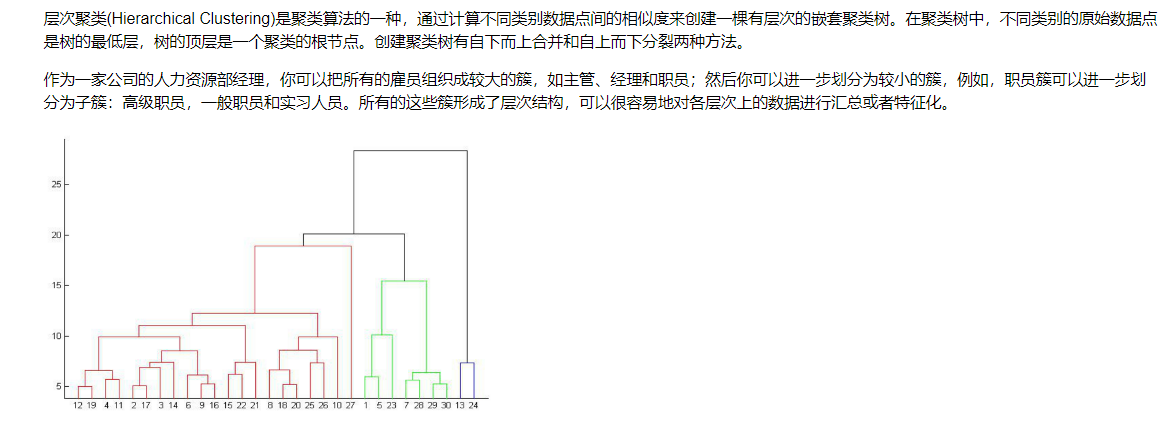
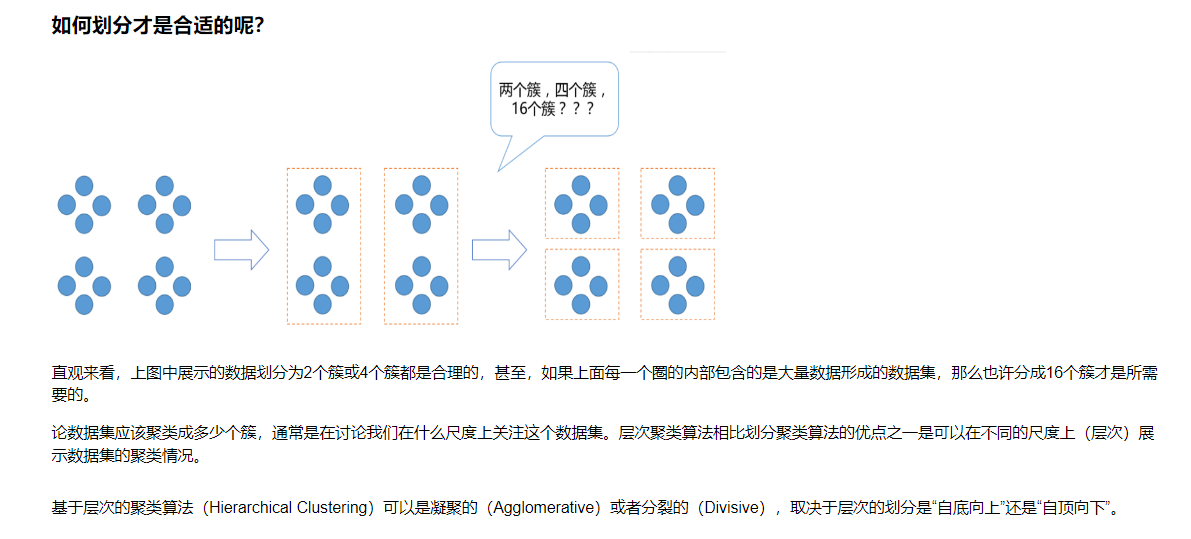
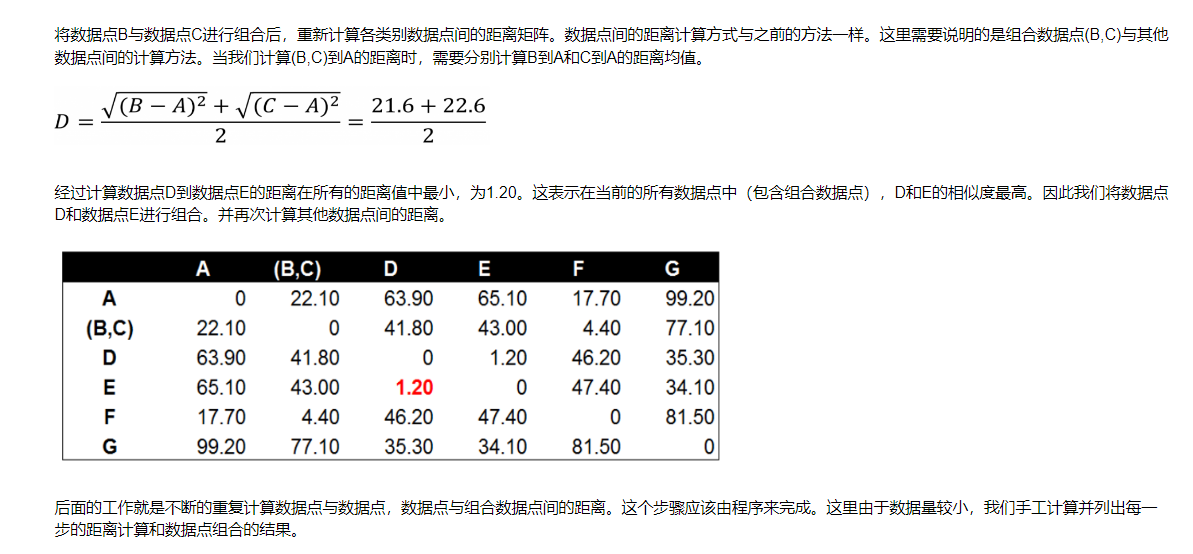
实例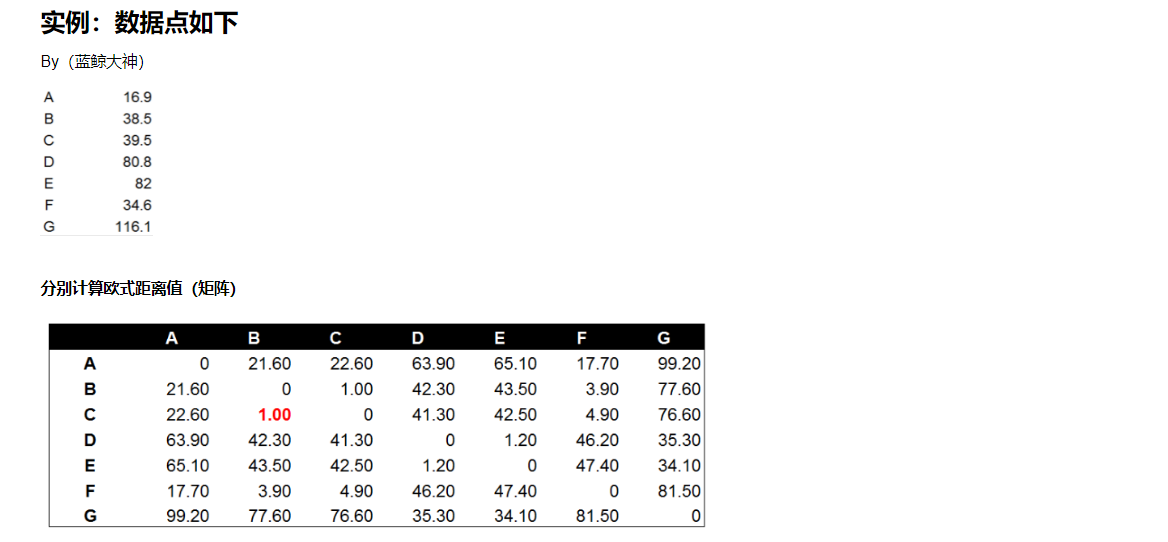

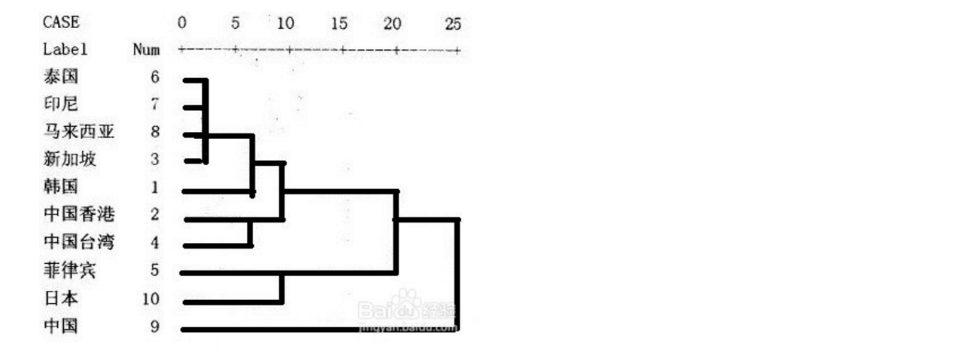
13.1.1 树状图

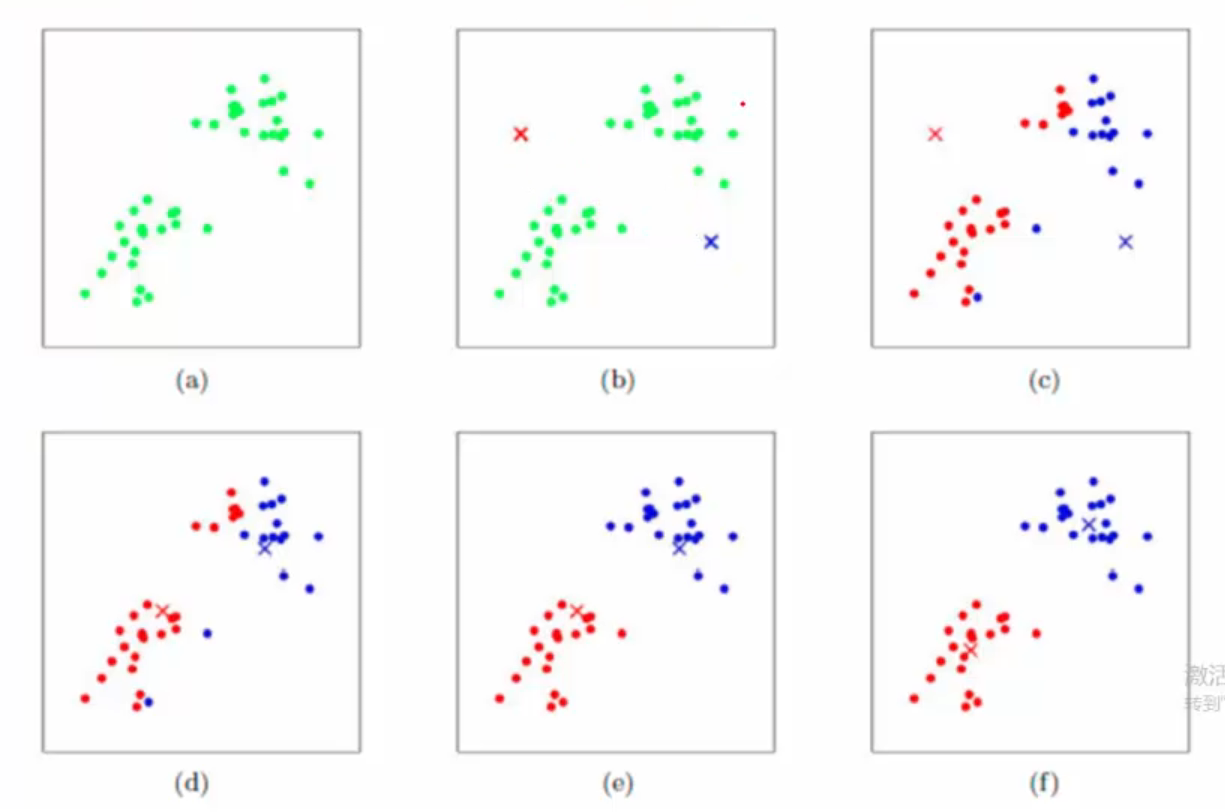
13.2 K-means算法

13.2.1 基本概念

13.2.2 工作流程

13.2.3 优缺点

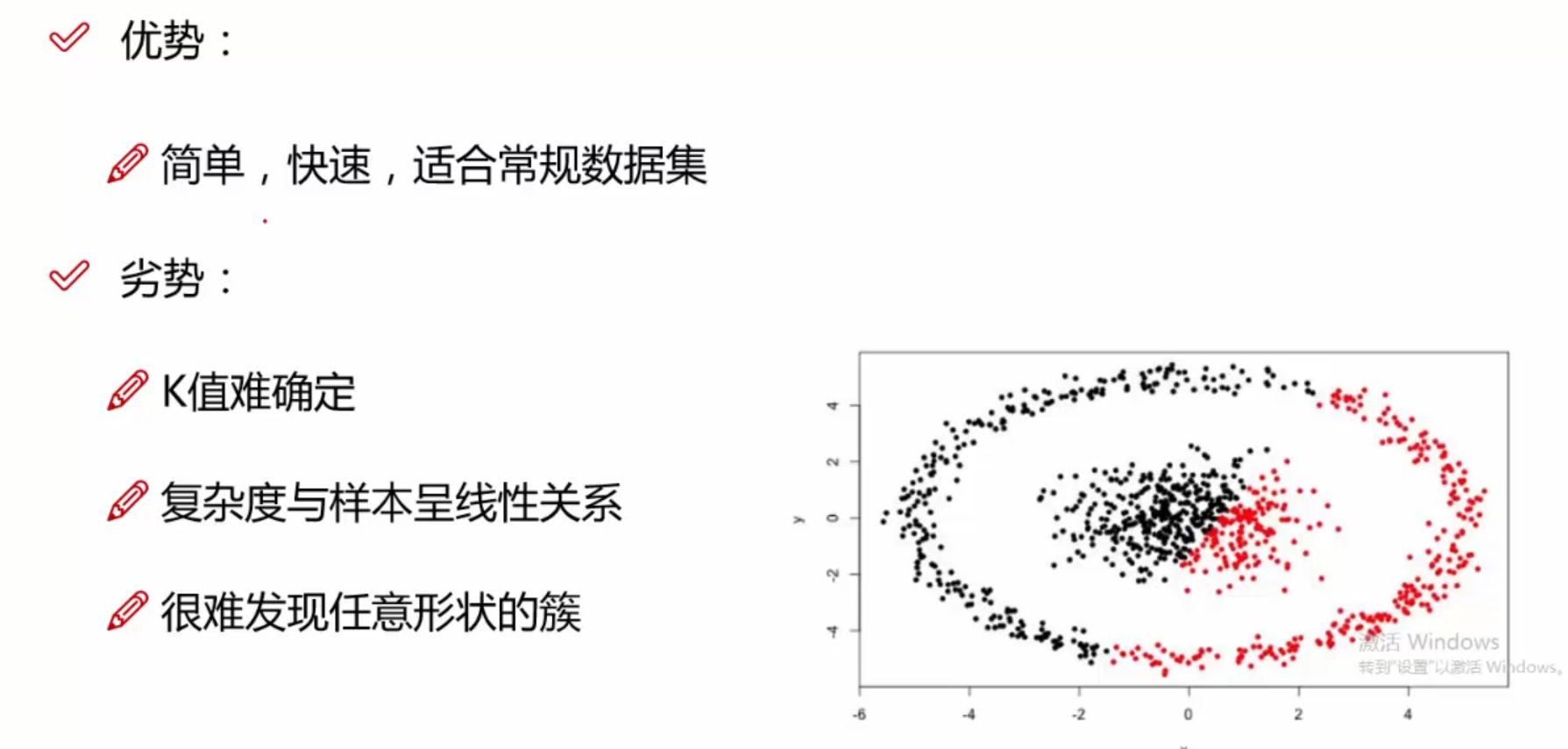
13.3 DBSCAN算法

13.3.1 基本概念

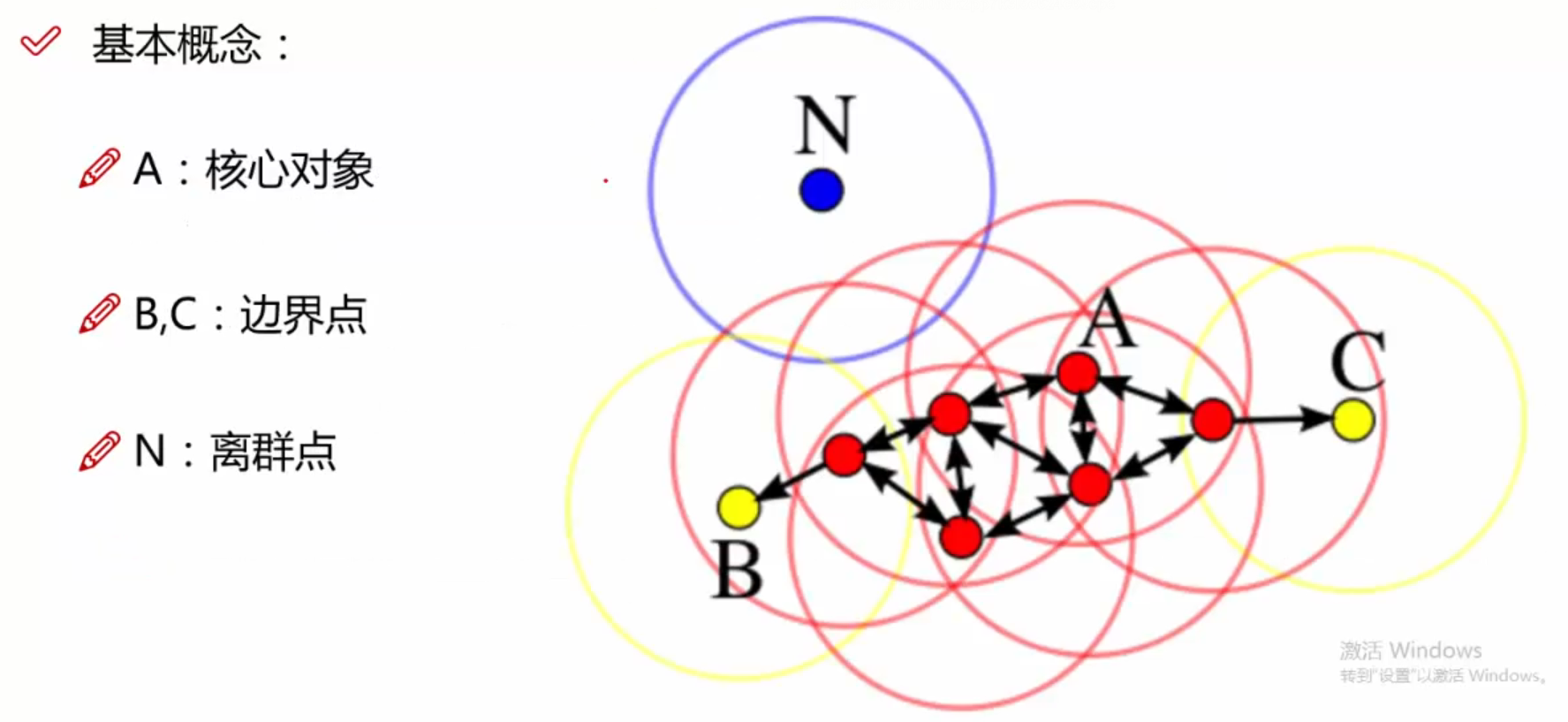
13.3.2 工作流程

13.3.3 优缺点

13.4 多种聚类算法概述

14.贝叶斯分析

14.1 基本概念

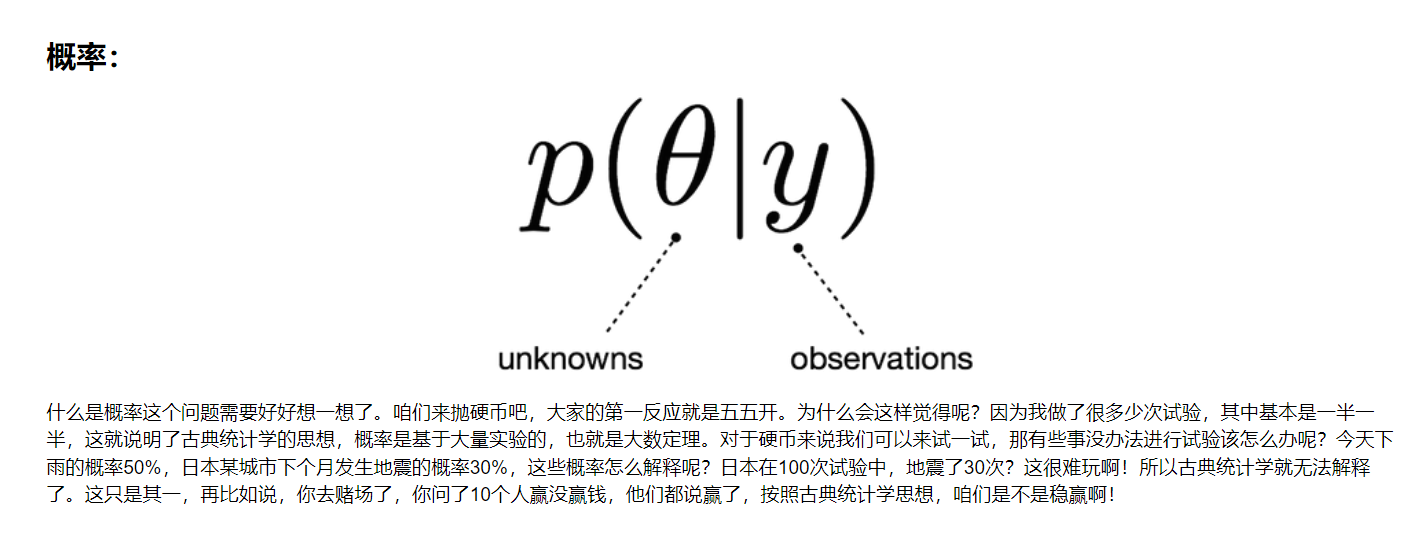
14.2 贝叶斯公式

14.3 贝叶斯推导

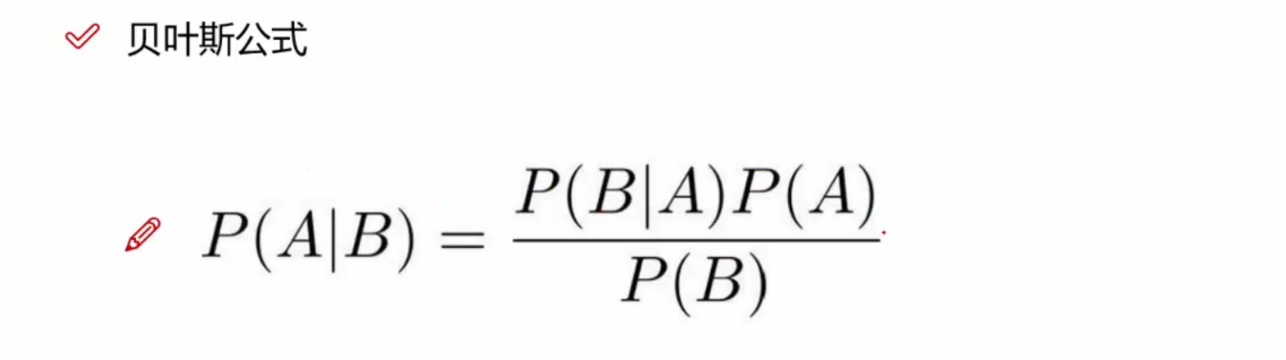
14.4 马尔科夫链蒙特卡洛方法MCMC

14.4.1 马氏链的平稳性