Solution Set - “女孩是瑰宝我心动一丝不苟”

目录

• 0.「NOI Simu.」静态顶树
• 1.「NOI Simu.」祖先
• 2.「NOI Simu.」睡眠
• 3.「JLOI 2008」「洛谷 P3881」CODES
• 4.「ARC 163A」Divide String
• 5.「ARC 163B」Favorite Game
• 6.「ARC 163C」Harmonice Mean
• 7.「ARC 163D」Sum of SCC
• 8.「NOI Simu.」国王的旅行
• 9.「NOI Simu.」图
• 10.「NOI Simu.」计算
• 11.「NOI 2006」「洛谷 P2703」千年虫
• 12.「HEOI 2014」「洛谷 P4102」林中路径
• 13.「BalticOI 2011」「洛谷 P4672」Tree Mirroring
• 14.「CF 1637H」Minimize Inversions Number
• 15.「HEOI 2015」「洛谷 P4110」小 L 的白日梦

\[\text{1 1 4 5 1 4}
\newcommand{\op}[1]{\operatorname{#1}}
\newcommand{\son}[0]{\op{son}}
\newcommand{\str}[1]{\underline{\texttt{#1}}}
\]

  打一首中 V 曲, 送分题!

0.「NOI Simu.」静态顶树

• Private link & Submission.
• 「A.DP-动态 DP」

  为什么静态 top tree 题不用静态 top tree 做呢?

  不妨对每个值域的 \(1\) 考虑贡献, 枚举 \(k\), 求出所有划分方式下连通块数量之和, 这个再对以每个点作为顶点的连通块考虑贡献. 设 \(f(u)\) 表示以 \(u\) 为顶点的合法连通块总贡献, \(g(u)\) 表示 \(u\) 子树内所有连通块的总贡献. 不妨设 \(1\) 为根, \(s_u\) 表示 \(u\) 子树大小, 考虑转移:

• 当 \(a_u\ge k\) 时:

  \[f(u)=\prod_{v}(f(v)+2^{s_v-1}),\quad g(u)=\sum_{v}g(v)+2^{n-s_u-[u\neq 1]}f(u).
  \]

• 当 \(a_u<k\) 时:

  \[f(u)=0,\quad g(u)=\sum_{v}g(v).
  \]

  结合题目名, 使用全局平衡二叉树 (静态 top tree) 维护 DDP 即可. 维护的向量是 \(\begin{bmatrix}f(u)+2^{s_u-1}&g(u)&1\end{bmatrix}^T\), 瓶颈其实在一个地方的求逆元, 但也不是不能优化, 复杂度是 \(\mathcal O(n\log n)\).

1.「NOI Simu.」祖先

• Private link & Submission.
• 「A.树论-树链剖分」

  设 \(w_u\) 表示 \(u\) 子树点权和, 那么 \(u\) 的答案为:

\[\textit{ans}_u=\frac{1}{2}\left(w_u^2-a_u^2-\sum_{v\in\son(u)}w_v^2\right).
\]

  不想树剖怎么办? 使用毛毛虫剖分支持菊花查(/修)+链修(/查)+子树修(/查), 然后就只需要线段树维护 \(w\) 了. 打两种标记, 比较繁琐, 不好看啦确实. \(\mathcal O(m\log^2n)\).

2.「NOI Simu.」睡眠

• Private link & Submission.
• 「A.数学-生成函数」

  不妨算非法方案, GF 会方便一点:

\[\textit{ans}=[x^Ny^{n-1}]\frac{1}{1-y}\prod_{i=1}^m\left((1-p_i)\cdot\frac{1-x^{a_i+1}}{1-x}+p_i\cdot\frac{1-(xy)^{a_i+1}}{1-xy}\right).
\]

  联系题目中 \(d\) 这个诡异条件, 可以发现暴力卷分子是可行的, 我们先求出 \(F_a(x,y)\) 表示有 \(a\) 项分子来自 \(\frac{\cdots}{1-xy}\) 时, 所有分子乘积之和. 那么, \([x^{N-u}y^{n-1-v}]F_a(x,y)\) 对答案的贡献系数是:

\[g(u,v)=[x^uy^v]\frac{1}{1-y}\cdot\frac{1}{(1-x)^{m-a}}\cdot\frac{1}{(1-xy)^{a}}.
\]

  代数推导灭天地, 组合意义保平安. \(g(u,v)\) 描述的是: 总共 \(u\) 个球放入 \(m\) 个盒子, 前 \(a\) 个盒子最多放 \(v\) 个的方案数. 枚举第 \(u-v\) 个球所在的盒子编号 (也许枚举第 \(v\) 个更符合直觉, 你可以试试, 应该不如这个方便), 有

\[g(u,v)=\sum_{k=1}^{m-a}\binom{u-v-1+k-1}{u-v-1}\binom{v+m-k}{v}.
\]

把 \(a\) 放在最内层递推即可. 不过组合意义还是有风险: 这个递推式对 \(u,v,a,0\) 的大小关系很敏感, 需要一些特判. 计算次数量级 \(10^8\), 题目硬凑出几个 \(100\) 当复杂度咱就不写出来了, 挺丑的.

3.「JLOI 2008」「洛谷 P3881」CODES

• Link & Submission.

  啊?

  \(f(s)\) 表示两种不同表示法的前缀都吻合, 其中一个是另一个末尾添加上字符串 \(s\) 时, 较短者的最优形式. Dijkstra 大力转移即可. 最坏 \(\mathcal O(n^5\log n)\), 实际上很快很快.

4.「ARC 163A」Divide String

• Link & Submission.

  只会分成两部分, \(\mathcal O(n^2)\) 大力检查.

5.「ARC 163B」Favorite Game

• Link & Submission.

  只会减小 \(a_1\) 或增大 \(a_2\), 枚举最终的 \([a_1,a_2]\) 求最优答案. \(\mathcal O(n\log n)\).

6.「ARC 163C」Harmonice Mean

• Link & Submission.
• 「A.构造」

  乐, 这种小 trick 不熟悉肯定是文化课学少了.

  特判 \(n\le 2\), 其余情况裂项构造 \(\sum_{k=1}^{n-1}\frac{1}{k(k+1)}+\frac{1}{n}=1\). 这在 \(n=a(a+1)\) 时会出现问题, 此时 \(2a(a+1)-2\) 一定不是 \(2b(b+1)\), 所以构造 \(\sum_{k=1}^{n-2}\frac{1}{2k(k+1)}+\frac{1}{2}+\frac{1}{2(n-1)}\) 即可. \(\mathcal O(n)\).

7.「ARC 163D」Sum of SCC

• Link & Submission.

  竞赛图 \((V,E)\) 的 SCC 数量等于将 \(V\) 划分为有序可空集合对 \((X,Y)\), 使得 \(X\times Y\subseteq E\) 的方案数\({}-1\). 随便 DP. \(\mathcal O(n^5)\).

8.「NOI Simu.」国王的旅行

• Private link & Submission.
• 「A.构造」

  Motivation: 限制最强的时候, \(k=nm-[2\nmid nm]\), 不妨先研究此时的构造.

  Observation: 注意到, 在这种情况下, 路径覆盖了矩形内几乎所有格子 (存在至多一个未被覆盖, 此时可以通过上下翻转构造路径来将其覆盖, 此后不表), 而路径是环, 所以几乎所有的起点都可以用这种路径构造方案. 因此, 我们只需要考虑起点是 \((1,1)\) 的情况.

  具体构造不必多言, 给出两个结果:

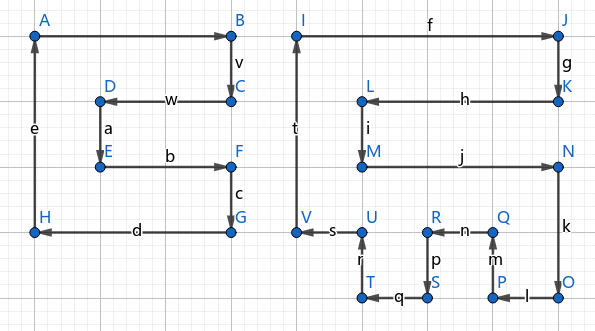
  最后的问题在于 \(k<nm-[2\nmid nm]\) 该如何处理. 我们不妨从限制最强的 \(k=nm-[2\nmid nm]\) 向小调整. 注意到在上面两种构造中, 我们可以不断消除任意 \(\str{L?R}\), \(\str{R?L}\), \(\str{U?D}\), \(\str{D?U}\) 子串而保持路径合法. 感受这股劲, 这两种构造都可以按照栈顺序不断被消除直到什么都不剩, 所以方案一定存在.

  顺带一提, 上述方案自然不是唯一的. 事实上, 只要 \(2\mid nm\) 或者空出来的一个格子在矩形的边界上, 都可以使用这种调整法调整出答案. \(\mathcal O(k)\) (可以根据 \(k\) 先人为缩小 \(nm\) 的范围使其和 \(k\) 同阶).

9.「NOI Simu.」图

• Private link & Submission.
• 「C.思维」

  不妨设 \(d_0<d_1<\dots <d_{m-1}\), 我们尝试找到一种归纳的方式: 每次找出一些树边, 删除一些结点和 \(d\), 将结点数和 \(\{d\}\) 缩小, 得到另一个相同形式的问题.

  考虑这样构造: 对于 \(i>0\), \((x,x+d_i)\) 可以被替换为 \((x+d_0,x+d_i)\), 此时编号最小的 \(\min\{d_0,n-d_0\}\) 个点都向后连了恰好一条边, 我们可以把这些点删掉, 另所有 \(d_i\gets d_i-d_0\), 如此归纳. 当 \(d_0,d_1\) 的大小关系保持不变时, 我们可以快速地多次操作 \(d_0\). 当 \(d_0,d_1\) 的大小关系改变时, \(d_0+d_1\) 至少变成原来的 \(2/3\), 因此总共只会迭代 \(\log\) 次, 复杂度 \(\mathcal O(m\log n)\).

10.「NOI Simu.」计算

• Private link | 不想写啦!
• 「A.数学-数论」「A.数学-多项式」

  注意到所有 \(a\) 的出现奇数次的素因子集合相同, 枚举集合乘积 \(x\), 则 \(a_i/x\) 是任意 \([\lceil L/x\rceil,\lfloor R/x\rfloor]\) 内的完全平方数. 令 \(L\gets L-1\), 我们可以将这些 \(a\) 的总贡献表示成 \(P(L/x,R/x)\), 它可以 \(\mathcal O(\log k)\) 被计算.

  重点在于对枚举 \(x\) 的优化. 令积性函数 \(f(n)\) 有 \(F_p(z)=1+p^{k-1}z\), 则

\[\textit{ans} = \sum_{i=1}^Rf(i)P(L/i,R/i).
\]

使 \(f(n)\neq0\) 的 \(n\) 是 square-free 的, 我们在这里见识过一种较为通用的做法. 具体地, 尝试进行 Powerful Number 样的拟合, 发现 \(g(n)=n^{k-1}\) 满足 \(f(p)=g(p)\), 设 \(f=g\star h\), 那么

\[\sum_{i=1}^mf(i)=\sum_{i=1}^mh(i)\sum_{j=1}^{m/i}j^{k-1}.
\]

又因为 \(h(i)\neq0\) 的 \(i\) 一定是完全平方数, 所以

\[\sum_{i=1}^mf(i)=\sum_{i=1}^{\sqrt m}h(i^2)S_{k-1}(m/i^2).
\]

我们在上文链接里推导过, 这里直接套两层整除分块的复杂度上界有 \(\mathcal O(\sqrt R\log R)\), 不过 \(P(\cdot,\cdot)\) 实际上只和参数的根号有关, 内层可以做到 \(\mathcal O(R^{1/3})\), 这样算出来复杂度是 \(\mathcal O(R^{5/12})\), 还需要加上求 \(g\) 前缀和的多点求值, \(\mathcal O(R^{1/2}+(k+R^{1/4})\log^2k)\).

11.「NOI 2006」「洛谷 P2703」千年虫

• Link & Submission.
• 「A.DP-杂项」「B.Tricks」「C.性质/结论」

  原题的第一步转化假了, 我们就来做这个转化后的题目: 给定 \(\{a_n\}\), 每次操作可以选择一个 \(a_i\gets a_i+1\), 求将其变为峰谷交替且一段峰或谷内部值相同的序列至少需要操作多少次.

  状态少转移复杂的 DP 可能不如状态多转移简单的 DP 好优化, 可以从状态定义入手转化问题.

  设 \(f(i,j,0/1)\) 表示考虑了 \(\{a_{1..i}\}\), \(a_i=j\), \(i\) 是谷/峰时的最少操作次数. 枚举 \(k\ge a_{i+1}\) 就能完成转移.

  最后呢, 我们容易看出 \(j\) 的惰性移动的特点 (为了合法, 只需要卡在某个 \(a\) 值附近), 因而对于 \(f(i,\cdot,\cdot)\), 只需要选取 \(p\in[i-2,i+2]\) 中 \([a_p,a_p+2]\) 内的所有 \(j\) 更新状态就能求出最优解, \(\mathcal O(n)\). 证明略过.

  Trick: 就算不知道正确性, 也可以想到用 "听着难卡" 的贪心性质人为缩小状态数, 在这里的 #8 中我们也下意识采取了这种策略.

12.「HEOI 2014」「洛谷 P4102」林中路径

• Link & Submission.
• 「A.数学-线性代数」

  \(n\) 小 \(k\) 大, 感觉不弱于邻接矩阵上的快速幂. 先用组合意义拆平方, 设 \(A^{(k)}_{uv}\) 表示 \(k\) 以内步从 \(u\) 到 \(v\), 选择了 \(0\) 条特殊边的方案数, \(B^{(k)}_{uv}\), \(C^{(k)}_{uv}\) 分别表示选择了 \(1\) 条, \(2\) 条特殊边的方案数, 设 \(G\) 为图的邻接矩阵, 那么:

\[A^{(k+1)}=A^{(k)}+G^{k+1},\\
B^{(k+1)}=B^{(k)}+2(k+1)G^{k+1},\\
C^{(k+1)}=C^{(k)}+(k+1)^2G^{k+1}.
\]

好消息是, 倍增时也是线性变换:

\[A^{(2k)}=A^{(k)}+A^{(k)}G^k,\\
B^{(2k)}=B^{(k)}+B^{(k)}G^k+2kA^{(k)}G^k,\\
C^{(2k)}=C^{(k)}+C^{(k)}G^k+kB^{(k)}G^k+k^2A^{(k)}G^k.
\]

\(\mathcal O(n^3\log k)\) 结束. 注意记录一些共同的中间计算结果减小常数.

13.「BalticOI 2011」「洛谷 P4672」Tree Mirroring

• Link & Submission.
• 「C.性质/结论」「C.细节」

  如果我们可以肯定 \(x,y\) 都不是叶子, 假设 \(x,y\) 是两侧树对应的结点, 我们可以通过点到 \(x,y\) 距离的大小关系判断其属于那棵树, 然后分别以 \(x,y\) 为根树 hash 判断树同构 (注意叶子是有标号的! WA 了十万次).

  如何对尽量少的 \((x,y)\) 进行尝试呢?

  首先判掉存在度数为 \(1\) 的点的情况, 合法图中一定只存在两个, 且它们为根, 直接检查就行.

  注意到在合法图中, 环是特殊的: 它一定对称横跨两棵树. 任意找出一个环, 特判环包含所有结点的情况, 此后删掉环上的边, 在合法图中一定存在一个连通块, 它恰好有两个点在环上, 且这两个点是相对应的. 我们只需要任意拿出这样一对点检查即可. \(\mathcal O(n)\).

  Corner 很多, 不要想着合法图判断图是否合法, 要有耐心!

14.「CF 1637H」Minimize Inversions Number

• Link & Submission.
• 「C.性质/结论」

  解题不行? 结论犹乏! 无以刻画? 边界转化!

  考虑 \(k=1\) 的情况, 我们只需要把一个数丢到最前面, 这里就不需要考虑被丢出去的数的相互作用了. \(p_i\) 被丢到前面, 全局逆序对的变化量为 \(d_i=\sum_{j=1}^i[p_j>p_i]-\sum_{j=1}^i[p_j<p_i]\), 我们选择变化量最大的一个数丢就行.

  \(k=2\)? 假设丢了 \(x<y\) 这两个位置, 我们发现如果先丢 \(x\), 再把 \(y\) 丢到 \(x\) 前面, \(x,y\) 的顺序就改变了, 嗯, 不合题意, 但这种情况下丢 \(y\) 时逆序对数变化量正如同 \(x\) 没有被丢过一样, 因为 \(x\) 总会从 "在 \(y\) 前面" 变到 "在 \(y\) 后面"!

  推广一下, 我们从左到右将下标集合 \(S\) 内的数丢到排列最前端, 逆序对变化量就是 \(\sum_{i\in S}d_i\), 非常独立.

  接下来, 我们还需要把 \(S\) 反序调整回题意要求的状态, 这里带来的变化量是 \(\binom{|S|}{2}-2\times{}\)子序列中的逆序对数. 我们需要最大化的就是 \(\sum_{i\in S}d_i-2\times{}\)子序列中的逆序对数.

  又不会了? 还有结论! 若原序列中逆序对 \(i<j\) 中的 \(i\in S\), 则 \(j\in S\). 反证+调整法 (调整 \(|i-j|\) 最小的 \(i\) 到 \(j\)) 可以证明.

  这样, 子序列中的逆序对数又和子序列本身无关了: 子序列中一个数向后的逆序对贡献就是它在原序列中向后的逆序对贡献! 这样每个数对变化量的总贡献可以独立刻画, 贪心地从大到小选取子序列即可. BIT 维护一些逆序对的求解, \(\mathcal O(n\log n)\).

15.「HEOI 2015」「洛谷 P4110」小 L 的白日梦

• Link & Submission.
• 「C.性质/结论」

  天高地迥, 觉结论之无穷; 信竞悲来, 识智力之有数. (滕王阁序背着太舒服了! 每天亿遍!!!)

  读对题: 活动序列是预先确定的, 不会随着女友前几日的表现动态决策. 因此, 对于给定序列 \(p_{1..k}\), 女友的期望不高兴次数为 \(\sum_{i=1}^{k-1}(1-p_i)p_{i+1}\).

  抄了一天题解了, 于是我们发现当选出的 \(\{p_k\}\) 集合确定时, 我们必然将它们不降地排列. 当 \(\sum p\) 一定时, 我们需要最大化 \(1\times p_1+\sum_{i=1}^{k-1}p_ip_{i+1}\), 利用排序不等式就得到这个结论.

  我们将所有活动按照 \(p\) 降序排列. 又有结论: 我们选择的一定是 \(p\) 的一段前缀和一段后缀. \(k>1\) 时, 不难说明第一个和最后一个必选. 不妨设我们选择了 \([1,l]\) 和 \([r,m]\), 中间散点最左侧位置是 \(i\), 后一个位置是 \(i'\); 最右侧位置是 \(j\), 前一个位置是 \(j'\):

• 若将 \(i\) 替换为 \(l+1\), \(\Delta=(1-p_l)p_{l+1}+(1-p_{l+1})p_{i'}-(1-p_l)p_i-(1-p_i)p_{i'}\), 当 \(\Delta\le0\), 有 \(1-x_l-x_{i'}\le0\);
• 若将 \(j\) 替换为 \(r-1\), \(\Delta=(1-p_{j'})p_{r-1}+(1-p_{r-1})p_r-(1-p_{j'})p_j-(1-p_j)p_r\), 当 \(\Delta\le0\), 有 \(1-x_{j'}-x_r\ge0\).

我们需要证明二者必成立至少一个:

• 当 \(x_l+x_r\ge1\) 时, 结合 \(x_{i'}\ge x_r\) 可知前者成立;
• 当 \(x_l+x_r\le1\) 时, 结合 \(x_{j'}\le x_l\) 可知后者成立.

  因此, 维护 \(l,r\), 根据 \(x_l+x_r\) 和 \(0\) 的大小关系扩展对应端点就行. 瓶颈是排序的 \(\mathcal O(n\log n)\).