poj3468 A Simple Problem with Integers（线段树/树状数组）

Description

You have N integers, A₁, A₂, ... , A_N. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

Input

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A₁, A₂, ... , A_N. -1000000000 ≤ A_i ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of A_a, A_a+1, ... , A_b. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of A_a, A_a+1, ... , A_b.

Output

You need to answer all Q commands in order. One answer in a line.

Sample Input

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

Sample Output

4
55
9
15

Hint

The sums may exceed the range of 32-bit integers.

Source

POJ Monthly--2007.11.25, Yang Yi

 

题目大意：

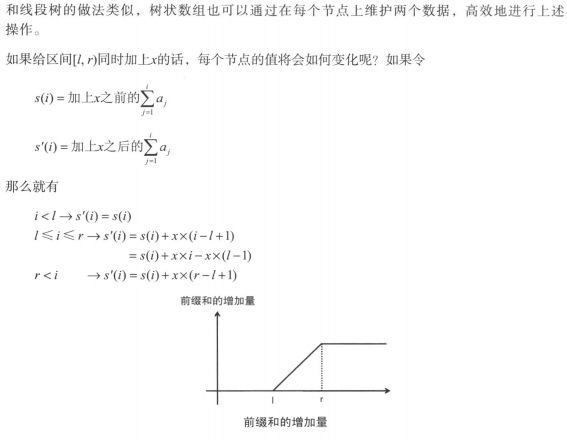
上图最后一行打错了，应该似乎求a[l]到a[r]的和。

线段树做法太裸，直接贴代码：

 program rrr(input,output);
 type
   treetype=record
      l,r:longint;
      sum,d:int64;
   end;
 var
   a:array[..]of treetype;
   c:array[..]of longint;
   n,q,i,x,y,d:longint;
   ch:char;
 procedure build(k,l,r:longint);
 var
   mid,i:longint;
 begin
    a[k].l:=l;a[k].r:=r;a[k].d:=;
    if l=r then begin a[k].sum:=c[l];exit; end;
    mid:=(l+r)>>;i:=k+k;
    build(i,l,mid);build(i+,mid+,r);
    a[k].sum:=a[i].sum+a[i+].sum;
 end;
 procedure pushdown(k:longint);
 var
   i:longint;
 begin
    if a[k].l=a[k].r then a[k].d:=;
    if a[k].d= then exit;
    i:=k+k;a[i].sum:=a[i].sum+(a[i].r-a[i].l+)*a[k].d;a[i].d:=a[i].d+a[k].d;
    inc(i);a[i].sum:=a[i].sum+(a[i].r-a[i].l+)*a[k].d;a[i].d:=a[i].d+a[k].d;
    a[k].d:=;
 end;
 function ask(k:longint):int64;
 var
   mid:longint;
   ans:int64;
 begin
    pushdown(k);
    if (x<=a[k].l) and (a[k].r<=y) then exit(a[k].sum);
    mid:=(a[k].l+a[k].r)>>;ans:=;
    if x<=mid then ans:=ask(k+k);
    if mid<y then ans:=ans+ask(k+k+);
    exit(ans);
 end;
 procedure change(k:longint);
 var
   mid,i:longint;
 begin
    pushdown(k);
    if (x<=a[k].l) and (a[k].r<=y) then begin a[k].sum:=a[k].sum+d*(a[k].r-a[k].l+);a[k].d:=d;exit; end;
    mid:=(a[k].l+a[k].r)>>;i:=k+k;
    if x<=mid then change(i);
    if mid<y then change(i+);
    a[k].sum:=a[i].sum+a[i+].sum;
 end;
 begin
    assign(input,'r.in');assign(output,'r.out');reset(input);rewrite(output);
    readln(n,q);
    for i:= to n do read(c[i]);readln;
    build(,,n);
    for i:= to q do
       begin
          read(ch,x,y);
          if ch='Q' then writeln(ask())
          else begin read(d);change(); end;
          readln;
       end;
    close(input);close(output);
 end.

下面是树状数组做法：

代码（实测比线段树快1倍）：

 program rrr(input,output);
 var
   a,b:array[..]of int64;
   n,q,i:longint;
   c:char;
   ans,x,y,z:int64;
 procedure adda(k,x:int64);
 begin
    while k<=n do begin a[k]:=a[k]+x;k:=k+k and (-k); end;
 end;
 procedure addb(k,x:int64);
 begin
    while k<=n do begin b[k]:=b[k]+x;k:=k+k and (-k); end;
 end;
 function suma(k:longint):int64;
 begin
    ans:=;
    while k> do begin ans:=ans+a[k];k:=k-k and (-k); end;
    exit(ans);
 end;
 function sumb(k:longint):int64;
 begin
    ans:=;
    while k> do begin ans:=ans+b[k];k:=k-k and (-k); end;
    exit(ans);
 end;
 begin
    assign(input,'r.in');assign(output,'r.out');reset(input);rewrite(output);
    readln(n,q);
    fillchar(a,sizeof(a),);
    fillchar(b,sizeof(b),);
    for i:= to n do begin read(z);adda(i,z); end;readln;
    for i:= to q do
       begin
          read(c,x,y);
          if c='Q' then writeln(suma(y)+sumb(y)*y-suma(x-)-sumb(x-)*(x-))
          else begin read(z);adda(x,-z*(x-));addb(x,z);adda(y,z*y);addb(y,-z); end;
          readln;
       end;
    close(input);close(output);
 end.