RSA公钥文件解密密文的原理分析

前言

　　最近在学习RSA加解密过程中遇到一个这样的难题：假设已知publickey公钥文件和加密后的密文flag，如何对其密文进行解密，转换成明文~~

分析

　　对于rsa算法的公钥与私钥的产生，我们可以了解到以下产生原理：

公钥与私钥的产生

1. 随机选择两个不同大质数 $p$ 和 $q$，计算 $N = p \times q$
2. 根据欧拉函数，求得 $r=\varphi (N)=\varphi (p)\varphi (q)=(p-1)(q-1)$
3. 选择一个小于 $r$ 的整数 $e$，使 $e$ 和 $r$ 互质。并求得 $e$ 关于 $r$ 的模反元素，命名为 $d$，有 $ed\equiv 1 \pmod r$
4. 将 $p$ 和 $q$ 的记录销毁

此时，$(N,e)$ 是公钥，$(N,d)$ 是私钥。

消息加密

首先需要将消息 $m$ 以一个双方约定好的格式转化为一个小于 $N$，且与 $N$ 互质的整数 $n$。如果消息太长，可以将消息分为几段，这也就是我们所说的块加密，后对于每一部分利用如下公式加密：

$$ n^{e}\equiv c\pmod N $$

消息解密

利用密钥 $d$ 进行解密。

$$ c^{d}\equiv n\pmod N $$

我们可以知道，RSA公钥主要有两个信息:模数(modulus)和指数(exponent)，也就是我们所说的N和e。只要有了这两个信息,我们便可以生成公钥，然后使用rsa库对数据进行加密~

脚本实现如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import rsa

key = rsa.PublicKey(modulus, exponent)
print key

这时候我们有如下的publickey.pem文件：

-----BEGIN PUBLIC KEY-----
MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgMBAAE=
-----END PUBLIC KEY-----

现在我们需要做的就是从这段字符串中提出模数和指数。

首先我们得知道pem文件是什么？

简单来讲，pem文件这种格式就是用于ASCII(Base64)编码的各种X.509 v3 证书。

文件开始由一行"-----BEGIN PUBLIC KEY-----“开始，由"-----END PUBLIC KEY-----"结束

pem类型的数据除去begin和end之外的内容，要根据base64编码解码后，得到的数据需要进行增加或裁剪特殊字符-、\n、\r、begin信息、end信息等。

这里有张图片很清楚的解释了这个问题~~

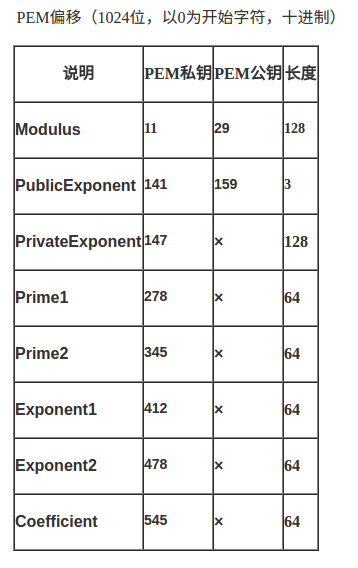
既然我们现在已经知道了pem这种文件格式，并且也知道其中的数据内容，我们该如何对这种文件内容进行解密呢？

我们可以做以下尝试Base64解码尝试：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import base64

pubkey = "MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgMBAAE="
b64_str = base64.b64decode(pubkey)
print b64_str
print len(b64_str)

解码以后如下：

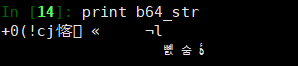
很明显，我们解出来一段乱码，我们尝试把这串乱码转换成16进制，这里我们用的是python自带的binascii库进行解码

发现结尾是"\x01\x00\x01",10001,看多了rsa的公钥,就知道这个数,多半是exponent了。

再看看解码后的长度为162,我们找到偏移表,发现模数的偏移位置是159，长度是3,加起来正好162~

那么说明这段字符串就是指数和模数加密过后的结果,甚至比一般的pem文件中的信息还要简单~

按照这个思路,对照偏移表我们找出指数e和模数N：

# /usr/bin/python
# -*- coding: utf-8 -*-

import base64

def str2key(s):
    # 对字符串解码
    b_str = base64.b64decode(s)

    if len(b_str) < 162:
        return False

    hex_str = ''

    # 按位转换成16进制
    for x in b_str:
        h = hex(ord(x))[2:]
        h = h.rjust(2, '')
        hex_str += h

    # 找到模数和指数的开头结束位置
    m_start = 29 * 2
    e_start = 159 * 2
    m_len = 128 * 2
    e_len = 3 * 2

    modulus = hex_str[m_start:m_start + m_len]
    exponent = hex_str[e_start:e_start + e_len]

    return modulus,exponent

if __name__ == "__main__":

    pubkey = "MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgMBAAE="
    key = str2key(pubkey)
    print key

结果如下：

('C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD', '')

这个即为我们求出来模数N和指数e。

当然我们也可以用一些比较方便的工具，Kali Linux里面自带了openssl，其他版本的Linux官方也提供了源码安装：https://github.com/openssl/openssl

而在Windows下安装大家可以参考这篇文章：https://bbs.csdn.net/topics/392193545?page=1，当然我还是不建议大家在Windows下进行操作，安装过程相对麻烦，而且可能安装过程中会出现各种状况~~~

我们使用如下命令对pubkey.pem找出指数e和模数N：

openssl rsa -pubin -text -modulus -in warmup -in pubkey.pem

结果如下：

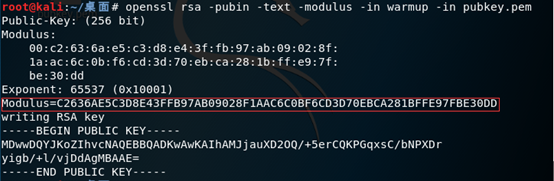
我们可以得到如下参数：

e=65537 (0x10001)

Modulus即为N=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD

然后我们可以使用yafu对n进行因数分解，得到p、q

p=275127860351348928173285174381581152299

q=319576316814478949870590164193048041239

解码网站在这里：https://factordb.com/

至此，各个参数已经求得如下，可以编写代码获得私钥，再用私钥解密密文，得到明文信息~

p = 275127860351348928173285174381581152299

q = 319576316814478949870590164193048041239

N = 87924348264132406875276140514499937145050893665602592992418171647042491658461

e = 65537

我们可以开始用python写脚本了~

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import gmpy2
import rsa

p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
N = 87924348264132406875276140514499937145050893665602592992418171647042491658461
e = 65537
d = int(gmpy2.invert((e,p - 1) * (q - 1)))
privatekey = rsa.PrivateKey(N,e,d,p,q)
s = open("flag.enc","rb")
print rsa.decrypt(s.read().privatekey).decode()

结果如下：

当然了，我们也可以用之前的公钥对一段信息进行加密操作，具体实现过程如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import rsa
import base64

message = 'Angel_Kitty'
key = ('C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD', '')
modulus = int(key[0], 16)
exponent = int(key[1], 16)
rsa_pubkey = rsa.PublicKey(modulus, exponent)
crypto = rsa.encrypt(message, rsa_pubkey)
b64str = base64.b64encode(crypto)
print b64str

加密结果如下：

这样子我们就得到一个rsa加密,base64编码过的字符串了，我们这个过程主要就是在一串字符串中,对照一个偏移表,提取需要的位置上的数字~~

本文用到的文件我已经上传到本地，点击下载即可：https://files.cnblogs.com/files/ECJTUACM-873284962/RSA公钥文件解密密文的原理分析实例.rar