Matlab:显(隐)式Euler和Richardson外推法变步长求解刚性问题

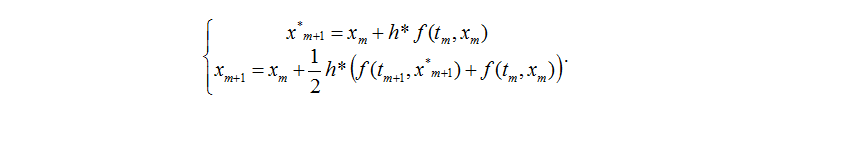
一、显示Euler

函数文件：Euler.m

 function f=Euler(h,Y)
 f(1,1)=Y(1)+h*(0.01-(1+(Y(1)+1000)*(Y(1)+1))*(0.01+Y(1)+Y(2)));
 f(2,1)=Y(2)+h*(0.01-(1+Y(2)^2)*(0.01+Y(1)+Y(2)));

脚本文件：

 tic;
 clear
 clc
 %%
 %显示Euler方法求刚性微分方程，要求用Richardson外推法估计近似误差从而控制步长
 y(1:2,1)=[0;0];%初值
 e=1e-5;%误差过小
 tol=1e-3;%指定的误差
 N=10;%节点的步数
 h=1/N;%初始步长
 t(1)=0;
 i=1;
 while t(i)+h<=1
     k=1;
     %%自动变步长
     while k==1
     y(1:2,i+1)=Euler(h,y(1:2,i));%符合误差的数值解
 y1_half=Euler(h/2,y(1:2,i));%半步长的中点数值解
 y1_one=Euler(h/2,y1_half);%半步长的右端点的数值解
 Estimate_error=2*norm(y(1:2,i+1)-y1_one);%中间估计误差
 if Estimate_error<tol%指定误差
     k=0;%步长相差不大，或者说正好在指定的误差范围内，则确定选择h作为步长。
 elseif Estimate_error<e%误差过小
     h=2*h;
 else
     h=h/2;
 end
     end
    t(i+1)=t(i)+h;
    i=i+1;
 end
 %%
 %绘图
 plot(t,y,'');
 xlabel('t'),ylabel('y(t) and z(t)');
 legend('y(t)','z(t)');
 title('Implicit Euler method for numerical solution of image');
 grid on;
 toc;

效果图：

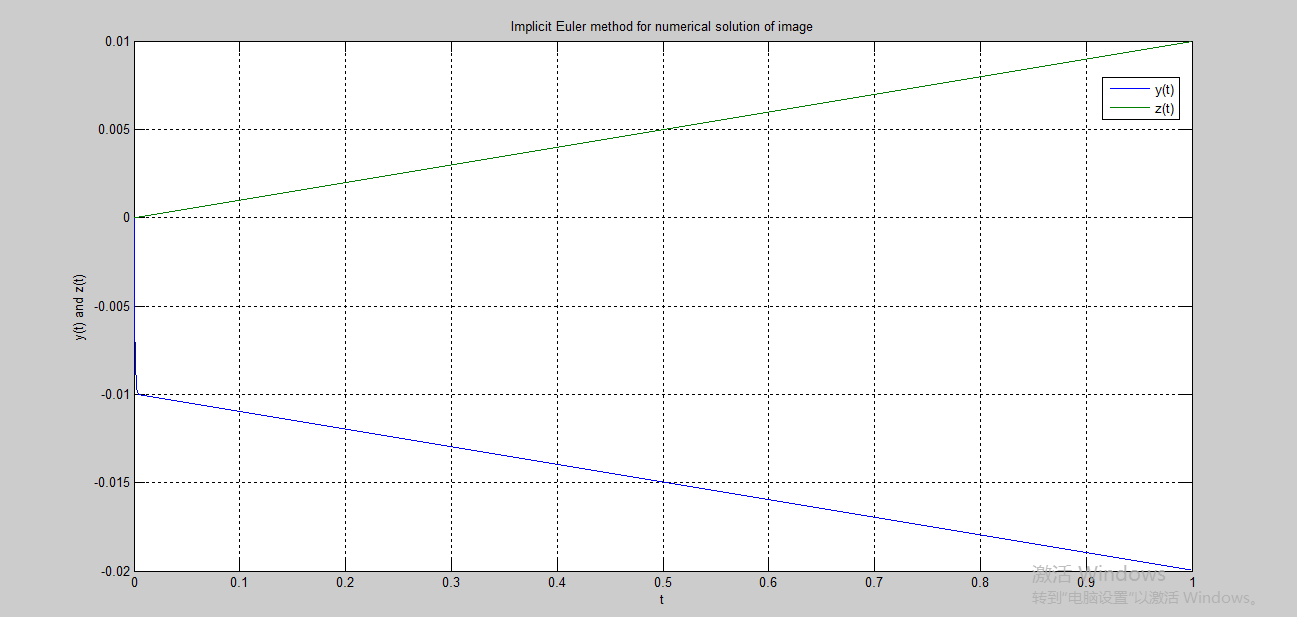
二、隐式Euler：Euler.m

 function X=Euler(t_h,u)
 %隐式Euler(Newton迭代法)
 %%
 Tol=1e-5;
 U=u;
 x1=U-Jacobian(U,t_h)\F(U,u,t_h);
 while (norm(x1-U,2)>=Tol)
     %数值解的2范数是否在误差范围内
     U=x1;
     x1=U-Jacobian(U,t_h)\F(U,u,t_h);
 end
 X=x1;%不动点
 %雅可比矩阵
 function f=Jacobian(U,t_h)
 f(1,1)=-t_h*((2*U(1)+1001)*(0.01+U(1)+U(2))+1+(U(1)+1000)*(U(1)+1))-1;
 f(1,2)=-t_h*(1+(U(1)+1000)*(U(1)+1));
 f(2,1)=-t_h*(1+U(2)^2);
 f(2,2)=-t_h*(2*U(2)*(0.01+U(1)+U(2))+(1+U(2)^2))-1;

 %方程组
 %%
 function fun=F(U,u,t_h)
 fun(1,1)=u(1)+t_h*(0.01-(1+(U(1)+1000)*(U(1)+1))*(0.01+U(1)+U(2)))-U(1);
 fun(2,1)=u(2)+t_h*(0.01-(1+U(2)^2)*(0.01+U(1)+U(2)))-U(2);

脚本文件：

 tic;
 clear
 clc
 %隐式Euler方法求刚性微分方程，要求用Richardson外推法估计近似误差从而控制步长
 %%
 y(1:2,1)=[0;0];%初值
 e=1e-5;%误差过小
 tol=1e-3;%指定的误差
 N=100;%节点的步数
 h=1/N;%初始步长
 t(1)=0;%初始节点
 i=1;
 while t(i)+h<=1
     k=1;
     %自动变步长
     while k==1
     y(1:2,i+1)=Euler(h,y(1:2,i));%符合误差的数值解
 % y1_half=Euler(h/2,y(1:2,i));%半步长的中点数值解
 y1_half=Euler(h/2,y(1:2,i));%半步长的右端点的数值解
 Estimate_error=2*norm(y(1:2,i+1)-y1_half);%中间估计误差
 if Estimate_error<tol%指定误差
     k=0;%步长相差不大，或者说正好在指定的误差范围内，则确定选择h作为步长。
 elseif Estimate_error<e%误差过小
     h=2*h;
 else%近似估计误差大于指定误差
     h=h/2;
 end
     end
    t(i+1)=t(i)+h;
    i=i+1;
 end
 %绘图
 %%
 plot(t,y);
 xlabel('t'),ylabel('y(t) and z(t)');
 legend('y(t)','z(t)');
 title('Explicit Euler method for numerical solution of image');
 grid on ;
 toc;

效果图：