快速傅立叶变换(FFT)算法

已知多项式f(x)=a₀+a₁x+a₂x²+...+a_m-1x^m-1, g(x)=b₀+b₁x+b₂x²+...+b_n-1x^n-1。利用卷积的蛮力算法，得到h(x)=f(x)g(x)，这一过程的时间复杂度为O(n²)。但是，利用分治策略和插值法来求解h(x)，可以将时间复杂度降低至O(nlogn)，从而大幅提升算法的效率。此求值算法将被应用于FFT算法中。

一、多项式求值

---

首先，由lagrange插值法可以知道，对于一个n-1次多项式，只要给定n个不同的点(x_i, y_i)，我们就可以计算出多项式的系数。因此，求解2n-1次多项式系数的问题，可以转化为多项式对1的复数域中所有2n次方根求值的问题。其中，1在复数域的2n次方根可以表示为

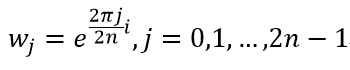
设f(x)，g(x)为n-1次多项式，则插值法求多项式h(x)=f(x)g(x)的系数的步骤如下：

1. 选择2n个不同的值x_j（j=0,1,...,2n-1），求出算f(x_j)，g(x_j)
2. 计算所有h(x_j)=f(x_j)g(x_j)
3. 由于h(x)的次数不高于2n-1，利用lagrange插值公式求出h(x)的系数

在第一步多项式求值过程中，如果用蛮力算法，即直接计算每一个A(w_j)，那么时间复杂度为O(n³)。但事实上，设A_k(x)=a_n-k+a_n-k+1x+...+a_n-1x^k-1，则存在关系：

A_k(x)=a_n-k+xA_k-1(x)

利用这一递推关系式来求解A(x)=A_n(x)，复杂度可以降低到O(n²)。这比蛮力算法已经有了很大的改进，但有没有更高效的求值算法呢？

采用分治策略，可以将多项式求值过程的时间复杂度降低至O(nlogn)，从而大幅提升算法的效率。这一算法的思想如下：

设要求值的多项式为A(x)=a₀+a₁x+...+a_n-1x^n-1，不妨设n为偶数，令

A₀(x)=a₀+a₂x+a₄x²+...+a_n-2x^(n-2)/2

A₁(x)=a₁+a₃x+a₅x²+...+a_n-1x^(n-2)/2

则

A(x)=A₀(x²)+xA₁(x²)

值得注意的是，根据复数域2n次单位根的性质，x²并不需要重新计算，只要在单位圆上间隔取值就可以了。下面给出用分治策略为多项式求值的算法伪码

算法1 Polyval(A, W) //分治策略多项式求值（假设n为偶数）

输入：n-1次多项式A的系数a₀,a_1,...,a_n-1，以及w₀,w₁,...,w_2n-1

输出：A(w₀),A(w₁),...,A(w_2n-1)

1. if A的长度=1 return A(W)

2. else do

3.     计算W₁: W[0]²,W[1]²,...,W[2n-1]²

4.     计算A0: A[0],A[2],...A[n-2]

5.     计算A1: A[1],A[3],...A[n-1]

6.     A0(W1)←Polyval(A0, W1)

7.     A1(W1)←Polyval(A1, W1)

8.     return A(W)=A0(W1)+W^TA1(W1)

算法的递推方程为T(n) = 2T(n/2) + f(n), T(1) = O(1)。其中，f(n)为初始时计算所有2n次方根的时间，f(n) = O(n)。根据主定理，得到T(n) = O(nlogn)。

二、快速傅立叶变换

---

设f(x)=a₀+a₁x+a₂x²+...+a_n-1x^n-1, g(x)=b₀+b₁x+b₂x²+...+b_n-1x^n-1，h(x)=f(x)g(x)。下面给出FFT算法的伪码：

算法2 FFT

1. 对x=w_j（j=0,1,...,2n-1），分别计算f(w_j)，g(w_j)

2. 利用步骤1的结果，计算所有d_j=h(wj)

3. 构造多项式D(x)=d₀+d₁x+d₂x²+...+d_2n-1x^2n-1

4. 对x=w_j（j=0,1,...,2n-1），计算D(w_j)

5. 设h(x)的系数为c₀,c₁,...,c_2n-1，则有c₀=D(1)/2n，c_2n-1=D(w₁)/2n，...，c₁=D(w_2n-1)/2n

不难分析，FFT算法时间复杂度为O(nlogn)。