Nginx源码结构及如何处理请求






Nginx源码结构及如何处理请求的更多相关文章
- Nginx源码结构
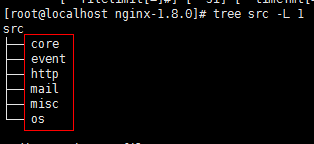
上一章对Nginx的架构有了一个初步的了解.这章,为了对源码仔细的剖析,先要对Nginx的源码结构有一个了解.从宏观上把握源码模块的结构. 一.nginx源码的3个目录结构 在安装的nginx的目录下 ...
- flask 源码浅析(flask 如何处理请求(多线程,多进程,IO多路复用))
2018-04-04 13:09:47 lucky404 阅读数 5724更多 分类专栏: python 版权声明:本文为博主原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接 ...
- nginx源码学习_源码结构
nginx的优秀除了体现在程序结构以及代码风格上,nginx的源码组织也同样简洁明了,目录结构层次结构清晰,值得我们去学习.nginx的源码目录与nginx的模块化以及功能的划分是紧密结合,这也使得我 ...
- nginx源码分析-源码结构
本文主要简单介绍nginx源码目录结构.程序编译流程.如何构建学习nginx的环境等.本文以及后续nginx源码分析文章是基于nginx当前(2009-02-27)的稳定版本0.6.35进行的分析,该 ...
- nginx源码分析之网络初始化
nginx作为一个高性能的HTTP服务器,网络的处理是其核心,了解网络的初始化有助于加深对nginx网络处理的了解,本文主要通过nginx的源代码来分析其网络初始化. 从配置文件中读取初始化信息 与网 ...
- Nginx源码分析:3张图看懂启动及进程工作原理
编者按:高可用架构分享及传播在架构领域具有典型意义的文章,本文由陈科在高可用架构群分享.转载请注明来自高可用架构公众号「ArchNotes」. 导读:很多工程师及架构师都希望了解及掌握高性能服务器 ...
- nginx源码分析之hash的实现
nginx实现了自己的hash数据结构,正如数据结构中讲述的那样,nginx用开放链表法解决冲突,不过不同的是一旦一个hash表被初始化后就不会被修改,即插入和删除,只进行查询操作,所以nginx通过 ...
- nginx源码安装
1,首先解决系统环境: 安装rpm包组{CentOS6 跟开发相关的包组:} a. Development Tools #yum groupinstall "Development Too ...
- Nginx源码安装及调优配置
导读 由于Nginx本身的一些优点,轻量,开源,易用,越来越多的公司使用nginx作为自己公司的web应用服务器,本文详细介绍nginx源码安装的同时并对nginx进行优化配置. Nginx编译前的优 ...
随机推荐
- 摘录和再编:彻底弄懂JS执行机制
网文: https://juejin.im/post/59e85eebf265da430d571f89 并发模型和事件循环:https://developer.mozilla.org/zh-CN/do ...
- ranch 源码分析(二)
接上ranch 源码分析(一) 上次讲到了ranch.erl的start_listener函数,下面我们详细分析下这个函数 -module(ranch). %...... 省略若干行 -spec st ...
- React文档(九)list和key
首先,我们回顾一下在js里如何转换数组. 给出下面的代码,我们使用map()函数来获取一个数组的numbers然后将值变成两倍大.我们分配新数组由map()返回: const numbers = [1 ...
- learning makefile VPATH
- SQL语句中Left join,right join,inner join用法
转载于:https://blog.csdn.net/lichkui/article/details/2002895 一.先看一些最简单的例子 例子 Table Aaid adate 1 ...
- unity中实现场景之间加载进度条
using UnityEngine; using System.Collections; using UnityEngine.SceneManagement; using UnityEngine.UI ...
- [BZOJ1406]密码箱
Problem 给你1个数n,求出0 ≤ x < n,并且x ^ 2 % n = 1 Solution x ^ 2 - 1 = kn,(x - 1) * (x + 1) = kn 所以枚举n的约 ...
- VMware与Centos系统安装、重置root密码
VMware与Centos系统安装 今日任务 .Linux发行版的选择 .vmware创建一个虚拟机(centos) .安装配置centos7 .xshell配置连接虚拟机(centos) 选择性 ...
- cocos2d-x js 中创建node的方法
1.精灵Sprite 一共4种创建方式 (1) 根据图片资源路径创建 1 2 3 4 //参数1:图片资源路径 var sprite1 = cc.Sprite.create("res/zif ...
- 用记事本编写helloworld文件但是javac时报错
刚开始编写第一个java文件时遇到的错误: javac HelloWorld.java HelloWorld.java:1: 错误: 写入HelloWorld时出错: HelloWorld.class ...
