HDU 6073 Matching In Multiplication（拓扑排序）

Matching In Multiplication

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 1127    Accepted Submission(s): 325

Problem Description

In the mathematical discipline of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V (that is, U and V are each independent sets) such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. A matching in a graph is a set of edges without common vertices. A perfect matching is a matching that each vertice is covered by an edge in the set.

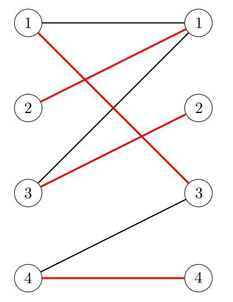
Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges' weight, and the weight of a graph is the sum of all the perfect matchings' weight.
Please write a program to compute the weight of a weighted ''bipartite graph'' made by Little Q.

Input

The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.
In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.
For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.

It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex.

Output

For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353.

Sample Input

1
2
2 1 1 4
1 4 2 3

Sample Output

16

【题意】给你一个二分图，每一集合里的 点数量 都为n，且其中一个集合里每个点的度数都为2.然后对于每一种完美匹配，算出边权值的乘积，然后再将每一种匹配的乘积加起来，输出最后结果。

【分析】U集合里的点 度数都为二，V集合里的点度数未知，但加起来肯定为2*n，对于V集合里度数为1的点，它的匹配对象是固定的，所以我们用拓扑排序将度数为1的点全部挖出，算出乘积res。然后对于剩下 的图，假设总节点为2*m，则V集合总度数为2*m，由于此时V集合里已经，没有度数为1的点，所以V集合里点的度数都为2，这说明这个图每个连通块是个环，在环上间隔着取即可，一共两种方案。比如对于两个联通块，他俩的两种方案乘积分别是(a1,a2),(b1,b2)，则答案为a1*b1+a1*b2+a2*b1+a2*b2,化简后为(a1+a2)*(b1+b2),最后在乘以res即可。

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define met(a,b) memset(a,b,sizeof a)
#define pb push_back
#define mp make_pair
#define inf 0x3f3f3f3f
#define qwer 2e18
using namespace std;
typedef long long ll;
const int N = 6e5+;
const int M = ;
const int mod = ;
const double pi= acos(-1.0);
typedef pair<int,int>pii;
int n,s;
int vis[N],in[N];
ll ans[];
vector<pii>edg[N];
ll topSort(){
    queue<int>q;
    ll ret=;
    for(int i=n+;i<=n+n;i++){
        if(in[i]==){
            q.push(i);
            vis[i]=;
        }
    }
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=;i<edg[u].size();i++){
            int v=edg[u][i].first;
            if(vis[v])continue;
            if((--in[v])==)q.push(v),vis[v]=;
            if(u>n)ret=(ret*1LL*edg[u][i].second)%mod;
        }
    }
    return ret;
}
void dfs(int u,int ty,int fa){
    vis[u]=;
    for(int i=;i<edg[u].size();i++){
        int v=edg[u][i].first;
        if(v==s&&v!=fa)ans[ty]=(ans[ty]*1LL*edg[u][i].second)%mod;
        if(vis[v])continue;
        ans[ty]=(ans[ty]*1LL*edg[u][i].second)%mod;
        dfs(v,ty^,u);
    }
}
int main(){
    //freopen("de.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        for(int i=;i<N;i++)vis[i]=in[i]=,edg[i].clear();
        for(int i=,v1,w1,v2,w2;i<=n;i++){
            scanf("%d%d%d%d",&v1,&w1,&v2,&w2);
            v1+=n;v2+=n;
            edg[i].pb(mp(v1,w1));
            edg[v1].pb(mp(i,w1));
            edg[i].pb(mp(v2,w2));
            edg[v2].pb(mp(i,w2));
            in[i]+=;
            in[v1]++;in[v2]++;
        }
        ll anss=topSort();
        for(s=;s<=n;s++){
            if(!vis[s]){
                ans[]=ans[]=;
                dfs(s,,);
                anss=anss*((ans[]+ans[])%mod)%mod;
            }
        }
        printf("%lld\n",anss);
    }
    return ;
}