L2-001 紧急救援（dijkstra算法)

题目：

作为一个城市的应急救援队伍的负责人，你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候，你的任务是带领你的救援队尽快赶往事发地，同时，一路上召集尽可能多的救援队。

输入格式:

输入第一行给出4个正整数N、M、S、D，其中N（2≤N≤500）是城市的个数，顺便假设城市的编号为0 ~ (N−1)；M是快速道路的条数；S是出发地的城市编号；D是目的地的城市编号。

第二行给出N个正整数，其中第i个数是第i个城市的救援队的数目，数字间以空格分隔。随后的M行中，每行给出一条快速道路的信息，分别是：城市1、城市2、快速道路的长度，中间用空格分开，数字均为整数且不超过500。输入保证救援可行且最优解唯一。

输出格式:

第一行输出最短路径的条数和能够召集的最多的救援队数量。第二行输出从S到D的路径中经过的城市编号。数字间以空格分隔，输出结尾不能有多余空格。

输入样例:

4 5 0 3
20 30 40 10
0 1 1
1 3 2
0 3 3
0 2 2
2 3 2

输出样例:

2 60
0 1 3

dijkstra算法：

dijkstra算法是贪心算法在求解路径问题上的应用。

作用：dijkstra算法能够解决边权非负的加权有向图的单起点最短路径问题。也就是说，规定一个起点，就能够得到这个加权有向图中其他点距该起点的最短距离。

数据结构：数组known[ ]用于标记这些点的状态（已知、未知）； 数组dis[ ]，也就是下表中的dv，表示每个点到起点的距离，附初值时，除了起点自身，其他的点到起点的距离都设为无穷，在实际编程时，可用定义一个很大的数（比如99999999）作为常量为其赋值；数组pre[ ]，也就是下表中的pv，表示引起dv变化的最后一个顶点，也就是以这种路径到达这个点经过的前一个点。

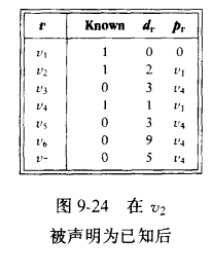
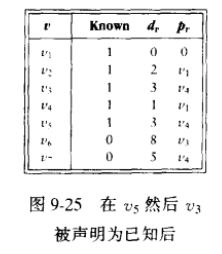
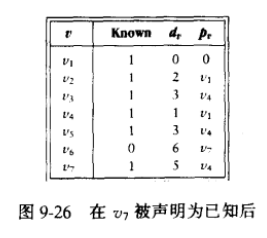
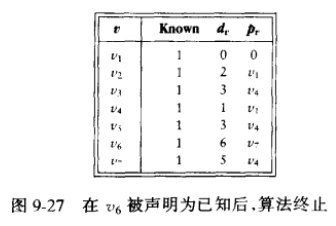
算法：以下面这个加权有向图为例，并假设开始结点为v1。初始配置如图9-12所示。每次更新下图的表格，算法都会选择未知的点中dv最小的一个标记为已知，然后去寻找这个点的下几个邻接点，如果该邻接点到这个已知点的距离加上这个已知点的dv小于该邻接点的dv，那么更新dv和pv，这其实就是从这个已知点这里走会更近的意思；如果该邻接点是已知的就跳过（因为每一次都是先将dv最小的点标记为已知，所以该点的dv不会更小）。

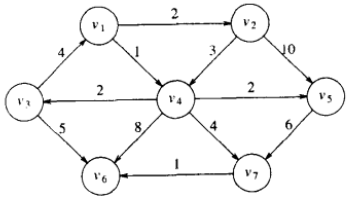
过程如图：

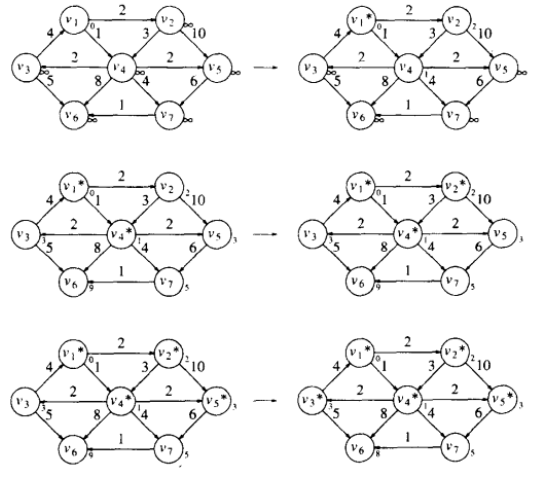
下表是每次更新的表格。在下面我直接把书上的讲解搬上来，书是《数据结构与算法分析：C语言描述》。

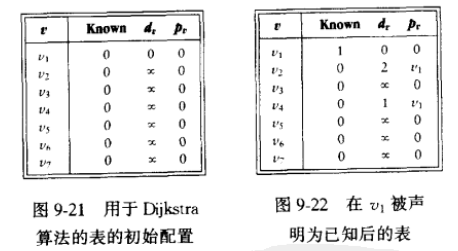
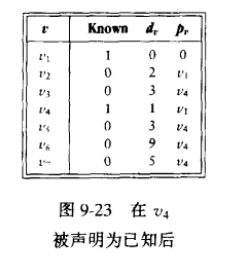
思路：

了解了dijkstra 以后，再来看这道题，发现题目就是在这个算法的基础上加了一个“救援队”和经过的结点数。那么我们在表格后多加两列就ok了，也就是在程序中加两个数组。最后按顺序输出路径那里使用了递归，具体见代码。

知识点for me：

1、fill()可以按照单元赋值，将一个区间的元素都赋同一个值，它在头文件<algorithm>里面。

它可以赋值任何，比如int数组：fill(arr, arr + n, 要填入的内容); 比如vector：fill(v.begin(), v.end(), 要填入的内容); 比如二维数组fill(f[0], f[0]+N*N, 要填入的内容);

　【C++】fill函数，fill与memset函数的区别 

上代码：

第一次写dijkstra，一些数组的命名感觉不是那么合适，将就看吧。

#include <iostream>
#include <algorithm>
using namespace std;
const int inf=;
int v,e,a,b;//点、边、起点、终点
int pv[];//路径中每个点的前一个点 

void printPath(int v)//递归输出路线
 {
    if(v == a) {
        printf("%d", v);
        return ;
    }
    printPath(pv[v]);
    printf(" %d", v);
}
int main() {
    cin>>v>>e>>a>>b;
    int help[v];//存储每个村的救援队
    int x=;
    for(int i=;i<v;i++)
    {
        cin>>x;
        help[i]=x;
     }
     int f,t,l;
     int dis[v][v];//边权
     fill(dis[],dis[]+v*v,inf);
     for(int i=;i<e;i++)
     {
         cin>>f>>t>>l;
         dis[f][t]=l;
         dis[t][f]=l;//注意！！道路是双向的！
      }
      int known[v]={};//最初所有的点都为未知
      int dv[v];
      fill(dv,dv+v,inf);//所有点到起点的距离除了起点自身是0，其余都是无穷
      dv[a]=;

      int min;
      int minn;
      int num[v];//累加的救援队的数量
      //num[a]=help[a];
      fill(num,num+v,help[a]);
      int way[v]={};//从出发点到v结点拥有的最短路径的条数
      for(int i=;i<v;i++)//dijkstra
      {
           min=inf;
           minn=-;
          //找出未知且dv最小的一个点，将它设为已知
          for(int j=;j<v;j++)
          {
              if(dv[j]<min&&known[j]==){
                  min=dv[j];
                  minn=j;
              }
           }
           if(minn==-)//如果剩下未知的点全是dv=inf，break
                   break;
           known[minn]=;
           for(int k=;k<v;k++)//找该点邻接的下一个顶点，并求其dv
           {
               if(dis[minn][k]!=inf&&known[k]==){
                   if(dis[minn][k]+min<dv[k])
                   {
                          dv[k]=dis[minn][k]+min;
                       pv[k]=minn;
                       num[k]=num[minn]+help[k];
                       way[k]=way[minn];
                    }
                else if(dis[minn][k]+min==dv[k]){
                    way[k]+=way[minn];//无论如何，到达k点的最短路径数量增加：原来的way[k]加上前一个结点的way
                    if(num[minn]+help[k]>num[k])//比较救援队的数量
                    {
                       pv[k]=minn;
                       num[k]=num[minn]+help[k];
                    }
                }
               }
           }

      }
    cout<<way[b]<<" "<<num[b]<<endl;
    printPath(b);
    return ;
}

杀不死我的使我更强大 _(:з」∠)_