spark实现smote近邻采样

一.smote相关理论

(1).

SMOTE是一种对普通过采样(oversampling)的一个改良。普通的过采样会使得训练集中有很多重复的样本。

SMOTE的全称是Synthetic Minority Over-Sampling Technique，译为“人工少数类过采样法”。

SMOTE没有直接对少数类进行重采样，而是设计了算法来人工合成一些新的少数类的样本。

为了叙述方便，就假设阳性为少数类，阴性为多数类

合成新少数类的阳性样本的算法如下：

1. 选定一个阳性样本ss
2. 找到ss最近的kk个样本，kk可以取5，10之类。这kk个样本可能有阳性的也有阴性的。
3. 从这kk个样本中随机挑选一个样本，记为rr。
4. 合成一个新的阳性样本s′s′，s′=λs+(1−λ)rs′=λs+(1−λ)r，λλ是(0,1)(0,1)之间的随机数。换句话说，新生成的点在rr与ss之间的连线上。

重复以上步骤，就可以生成很多阳性样本。

=======画了几张图，更新一下======

用图的形式说明一下SMOTE的步骤：

1.先选定一个阳性样本（假设阳性为少数类）

aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAkGBwgHBgkIBwgKCgkLDRYPDQwMDRsUFRAWIB0iIiAdHx8kKDQsJCYxJx8fLT0tMTU3Ojo6Iys/RD84QzQ5Ojf/2wBDAQoKCg0MDRoPDxo3JR8lNzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzf/wgARCADJASIDAREAAhEBAxEB/8QAGwABAQADAQEBAAAAAAAAAAAAAAEEBQYCAwf/xAAaAQEBAQEBAQEAAAAAAAAAAAAAAQQDAgUG/9oADAMBAAIQAxAAAAD9xAAAAAAAAIteQUAAAAAAAAAAAAAAAAYVnxefS7GegAAAAAAAAAAAABEkVbQkaDvw0/bhlc+vXZ9IAAAAAAAAAAAAEjj9GfE6+Oizd9146CCAtqAAAAAAAAAAaj1z47dk8x+kYN3pQAAAAAAABJAtFAAAAABJAW0AAAAAAAIYlnH68o7DJpzPPpQAAAAAAAAAAACFAAARBVAAAAAAAAAAAAA4LXjp1+XVmefdsAAAAAAAAAA/PdmL49PHUY9e/wCXS2gAAAAAACJwWnN6vnp82jazoAAAAAB5QWW2FAAAAAAAEiWURbSAoAAAAAAAAAAAAA0nvnz2jPl8+vY8O4GE88hqzSuvyas5QAAAAAAAAAAAAIgqgCQFCgAAEjWevPL680O9x6wABEhoOevBnXrevz6VQAAAIiKqgAAACSFCqAAJWr8+/wAUw/rcfx0/dPo/jtn68WAAABE5PvwtnRcO+VPQAAAAAAAAAGj8aMWdOm6YwAAAANZfCs3z7+wAAAAAAAAAB5QelAAAAAQAoAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACSa33EmZPX2l4jXm+frx0WbRuvHQAAAAAAE5/pz5bXl+3j1+h49oAAAAEk5LRn9V0OfRlSxBVtAAAAAACJPNtgtoAAAAAELAUAAABJNB158vsy5vHr3eXUAAAAAAAAABoevGVsOXTPnoAAAAkiCz09AAAAAAAAAAaHrxlbDl0z56AAAAAAAAAAAAAAAAELCgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAP/8QAOxAAAQMCAwIKCAUFAQAAAAAAAQIDBAURAAYSE9IUFRYhMUBBUlWUFzBQVGSSpeIHECBhlWBlcJOi0f/aAAgBAQABPwD2tLqESFpE2UxH130bZwI1W6bXPPbHH1G8Vg+YRhir02Q6GY1QiuuqvZDbyVE9psAeu3/VmSgLrTkZaJQY2AV0tar6rfuLWtjkI/4q35U7+KRlFyn1KPMXUEOhkk6AwU9KSnvHvddrOTTVKo/O4W0jbEHQqPr6EhPeGPR78ex5L7sZaovEcN6Ptw9reLlw3o6QBa1z3euZlemsUd9ynazJBRp2aNZsVAGwsezHGua/7n/HDcwqrZt0EoNS/jhuYHtYYqUngVPlStOssMrc0XtfSCbXx6QvgGPO/Zj0hfAMed+zFMk8Np8aXp0F9lLmnptqANsD2Hbricy5o8K+nP72OUmaPC/pz+9imOvyIEV6UgtvLZSp1FimyiASLHnFj1ednSoMTpTCTAAZfW2NaCVWSojvjHLup9+m/IrfxlGrv1qA+/J2OtD5bGxBAICUntJ7T1I4GZs0eFfT397HKTNHhn05/exQZMyZTGn6gzsZKiq6NBRYBRA5iSRcAH19va2ZIVQnw2m6XI2DodClHbKaumxFtSQT0kHHJrM/if1F/dxRaJXotUYfmz9cdBOtvhjrmoWIHSAP0VJp6TT5TMVezecaUltdyLKIIBuOcWOOTWZ/E/qD+7gZazN4p9Qf3cUxp6NT4zMpe0ebaSlxdybqAAJuec3Ps6vVI0mlvTdkHdmUDSVaQbqCemxtbHpC+AY879uFfiHpBPFzPnft9TnSryKJlyXUYQbLzOiwdBKedYGPw6zFMzNSH5c9tlDrb5aAZ/YDrA/K3qa+3Keos9FPvwtUdwM6FaSFkEJsbixv23GK7Rs6RaW8/WnJ5gjTtQ9ODiflCjjLNLzZNhLXlxyYIodsoMywyNfzDFAalM0WA3UL8LRHbD2tWolYACrm5ub9tz6onAz3T1o1CFO/438cuoPuM75Ub+IMpE2GxKbuEPNpcSCLGxAIv1bNVF5QUJ+mB/g+20naaNVrKBxkfLJytTHoZliSXXy7r0aOkAes4ho/hUDyyMcQUfwqD5ZGGm0MtpbaSEISAlKUiwAHMAAOgdXH9R8fUfxWD5hGOPqP4rB8wj/3DTiHm0uNKC0KAUlSTcEHnBBHSPymZ6MabIj8BZJZeU3dUrSTYkXtpOPSF8Ax537MZarXHkN6RsAzoeLdg5r6ADe9h3uoZuk1KNBZNK2u1L9lllnaHRpV2WV2gY41zX3ql5AbmINTzMqfFQ6Z5bL6A4FwQBpKgDc6B6y2BkSAlGkTZw+TcxyGg+/TvmRuYgxUQ4bEVu5Qy2ltJJuSEgAX/Kw9n5tq79GgMvRtjrW+GztgSkApUewjtGOXdT71N/1q38UHNk2o1iLDeMItvFQXskEKFkkgglR6s7mmjsvONOylhbaildmHCAQbEXAtjlfRPe3PLO7uKXU4lUZW9CdLiEq0ElCkkGwNrEA9BHrLdXdyrR3nnHXYqytxRUuz7gBJNybBVhjkhRPdHPMu72KZTIlLZWzCbLaFK1kFalkmwF7kk9AH+DP/xAAsEQABAwIEBAYCAwAAAAAAAAABAAIDESEEFEBREjAxUhATICJQYkFCYGFw/9oACAECAQE/APlgNl5Z2XARrr7emKXy1nDspcSXilNZ0UcwYOizf1Uj+I1p6KaiMCvuQZhfyU5mGpY/CWQohogsp9llPsjZD58RQ968mHv1EeGDhWqybe5SsDTQLpoQE2KMi7kYoR+yeGg251/C+lt8AxzQbrzoe1Pewiwp6GkAoSx9qM0XanFpPwVlZDlNbU0WU+yyn29Y8JHFrKhQOL2VKHLoFQcyqur8l7ZWtNSomyOb7UOULpuGeUcM8I200jeIUUbOAU5gcd1xHfTj+ScB2XA/ZEEIXUeFLxWqOEp+ykZwmldBEGk+5CPD7p8cNDwnmVoUMSWhZl5TiSfAH+1ffQgHWC6ijDjQrJsH7KaAMFQdMIZCKgLLy7Itp15Yqr7o6YTSAUBWYl3RdXr/AIZ//8QALREAAQMCAwYGAgMAAAAAAAAAAQACAwQRIUBREhMUMDFBBRAgUFJhYGIicHH/2gAIAQMBAT8A92Jst41bYztwrj0BSw7a4T7TKfZzr4i5cKR3TGBozkl7YIvqB0Ca+oviEL29jxWOU4r9VxX6ppv+AGWX4oSzfFDLuqHDsuKdoonlwxXXIk2TpnjoEJZT2TC4jHnYaKw0QtksFh5Y+wPa8jArdS6pjCOvocLhGJx7psTh3TRYe3E2XEn4oVJ+PIBKoqcT1DYybArxGkbTShjTdXKHKxVzywrKwVh6woSNoX6Kln8PfM1sQ/l/irJKGN9psTbRSlu0bdEeSTZGpDU2pBQN8tSz8NMJAL2VbVmqk2yLcwtCDAEMv9X/ACMyNCEjUDdEp0xauKJ7JjwRkJS4DBF8yY+XvzCLo090KeyAsPKwVhpkSRnZZC0YIVTj2UU1ziMtvotVv4tU11+WbIAaID6y25i0W4i0TW2/oz//2Q==" alt="" data-filename="1 (1).JPG" />

2.找出这个阳性样本的k近邻（假设k=5)。5个近邻已经被圈出。

aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAkGBwgHBgkIBwgKCgkLDRYPDQwMDRsUFRAWIB0iIiAdHx8kKDQsJCYxJx8fLT0tMTU3Ojo6Iys/RD84QzQ5Ojf/2wBDAQoKCg0MDRoPDxo3JR8lNzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzf/wgARCADkAUIDAREAAhEBAxEB/8QAGwABAAIDAQEAAAAAAAAAAAAAAAEFAwQGAgf/xAAaAQEBAAMBAQAAAAAAAAAAAAAAAQIDBAYF/9oADAMBAAIQAxAAAAD7iAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACAiUk2gAAAAAAAAAAAAAAAAAQnF9XNjz19By9NzhtAAAAAAAAAAAAhBKgDUTnujn8y9bz75tArMsBsY5bagAAAAAAAAAAAaLHFZlN6ZgYE08sRZYZTaAERZKgAAAAAAAAAAAcxv0V2/RY6NvTc/TNAAAAAAABECyZVAAAAAAAAQjGqWSoAAAAAAAiOe26aTfo3Ne3sdHQAAAAAAAAAAAAABCaialx9W2uOYAAAAAAAAAAAAEIJUAAAQlDsw5fp59nVn33P0gAAQglQAAAAAABEVGzXx/ZyeV+lcHcAAAANVNg9KAIk1a0M8Od6efJhl2/L1LCkmVQAAAAEIxqwTaAAAAEBQA5bbq8Za7PVuuMM5siK3KaezXkxt1r2TaAAAAARKsSqAAAAAAAHObNVds19Dp3WeGahWXDT2YZMbda9k2gAAAAI1cpqXHPLvTIAAAQSAAAAAAQhSTKoAAAACI4vo58G3VsatvaaOgAAeUptfR8b4/VfWevzXTbeMAAAAQky+T1YUAAAAAAYrK9Ns2pkAAPKc3r7fjvF6j6j1+e7fd8wAAAAUueHO9PLt4Z9hy9U0AAAAAAAAAAABVzOzuuVAAAAAAAAAAAAAAAAAAAhEs0AAAAAAAAAAAAAAAhQQoAAAAAABEUSVAAAAAAAAAFVlh7LLDNQAAAAAAFblhBmxy3VAAAAAAApc9fO9Ojb1Z9hz9FZlhxXVywv0nj7JoAAAQhZABByXRzau3Vcc/R0GrcAAAAAABEQk1KxJW5TIu9LIAAIivzwxLuS7UoAhJIlVIAAAAAAAAAAAAABEfPe3j1dmrp+Tr6bVuAAAAAAAAAAAFXceY6+Xyd7x9gAAAAJiNKrKUAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAD//EAEIQAAEDAgQBBwgGCAcAAAAAAAECAwQFEQAGEjETFSFAQVFV0hQWIDBQYYGUIjJSVGSlBxAXJHBxkuImM1Ngk6Sx/9oACAEBAAE/AP4HSs6PMS32BTULDTy29Rk/ZJF7aTjz7f7rb+aPgxlysGtQ3n1sBgtvFvSF6tgDe9h2+wJslEOHIlOAltltTigNyEgk2x58wfuM7+lHjwc9wEIKjCmj4I8eB6DlEpTji3XabDWtZJUtbCSSTuSSMCg0buqD8sjESHGhtlEOO0w2TcpaQEi/bYDpUmpwIbgblzYzCyL6XXUpJHbYnHL1H71g/MoxFqcCY4W4k2M+4BfS06lRA7bA+g60h5tTbqQtCgUqSoXBB5iCDuMcgUfuqD8ujHIFG7qg/Lo9g1/LDlXqAlompYsyGtJZ1bEntHbjzEf71b+VPjxl/LDlHqBlqmpeuyWtIZ0bkG+57PZAGB0PM9MqtQVGNLl8ANhfEHHW1qJtb6oOPNvNHef5g/4cUWi1+JVGH5lQ1x031t+WOuahYgcxAHT58lMSI6+UlegfRQN1E8wA/mSBhFPfeTrmTZBf3PBcU2hB7ABuB773xBdfRMchSnONZAcZdsAVJvYhQHNcG3OAAQR7HzdR3K3Swwy6lLjTgdAUm4WQCANxiHk1iUyXUVKMNP8AmIVDstHaFAquCMZZy0Ga0ie1LbXHjXCVoY0h0kFJsbm4Hb6i/Q8ywHapR34bBbDjhQRxCQnmUCbkA48xKn9mm/8AIrwYVkSprQRam/1q8Hq34ESQsOSIrDqxstbSSR/IkYACRYWAAsB6Tc6I86WmZTC3RuhLiSR8Ab4zLReXYbUbjBrQ8HLlvVsCLWuO3H7PPx7HyX92IWRTFmMSPLmSWXkuWTF0k6SDvqOB7ErlbpqJ6KbLkKSgEmUENr2sCEXA69QJw9XcsvMcAuaUj6umK4ko7CCE8xGMuVNFUpwcQ7xVNLLTi9JF1DrsQNwQfQqdZg0otic8UF2+izalbb7A4876J97c+Wc8OIWZKVOkoixpCy65cJBZWnYEncAewazlmFUXVSw3aWVJNy6sJXYAWIB5gQMHLLDoLbVGcYX1vOzVFA94AXdVuwhOKPSo1HieTxEkJKtS1FRJUqwBJueu3oVOjQaqWzPZKy1cIs4pNtW+xGPNCifdHPmXPFiFlulQZKJMZhYdbuUkvLVuCDuSPXTJKIbC33LkCwCUi5UomwAHWSbAYBq67uWht9YYVqJ+KwbD4JOKfLEttwlCmnm1lDrZNyhQ5/iCCCD1gj1JI6dnKnVN6YzLjS+FETw0EcdbYSvUoaiACANufHm3mjvP8wf8OMp02qRq1MdmS+K0hHCV+8Lcu5cEfWA2Hp3xXcy0mgFnlaSWOPfRZtStt9gcfpNrEGu19qXS3+OwIiW9innClHFKztQKtOagwJxdku30oLK0/wDoHrQegONoebUhxIUhQIKSLgg7gjHJOj6DU6a2x/opcFvgogqHwUMRYzUVkNMoSltOwA+JPvJPqM2ZQhZpMYzn5LRjatHBt1/zBxn+gRss1lqDCeecQqMHSXveVDFA/R1SqJVWKlGkzFvM3sHCkp5wR1JHq8y8reRtch34/GGvRo+pY/a5t7Y/xv8Aif8Aq4o3nXyoxyjxfI7ni6+B2H7PPv0udRaXUHQ7OpsSU6BpCnmErNuy5BOB/vNdRfcecZgRePw1aVuLXoQD1gGxJI67Cw2viJO4zyo7zKmJCRqLaiCCL2uFDmI6u0dY6C/VqbGeU1IqEVp1O6HHkpUOsXBN8cvUfvWD8yjESoRJpUIUpiRotr4LgXa97Xsea/QMy1rkOG1I4Id1vBuxc0bgm97Hsx+0P8Ax87/bijZyNUqjEHyRpHGJGtMjXskq20j9Vdiy5lMdYp7/AAZCimy9ZRYBQJ5wCRcAjFNoNfeigs1DRZSkqT5c8khQJuCAmwOJFAzCJbDIqNpCgsoInPEpTYAkkpv0GrZRdn1ORMRPQ0HiDoLBVskJ31Dsx5iP96t/Knx4y1QFUVcpa5Yf44Rs1otpv7ze9+g2GAP1vU1tT6n2H34zyyNa2SLK7CUqBST1XtfESA1EUpxOtby7anXFXUQNh7gOwWHqajJWzwmo6QuS8vS3qJAFuclVuoAfE2GFMVJlBdan+UubllxtKUH3JIGpPxKsQpKJcZt9u4S4AQDzEdoI7QeY+x81ZclP1pyf+68B9aE3dURpOkAavomwuLDD+TJsZlTrwpaGkAlSi4fBjI9MfpVIWiXoSXni8EIP1QQAAbgdJrsmXDpjr9PZ40lJTpb0FdwVAHmBBNgScecmaO6/y5/xYOZc0d1flz/i9Y42h1socSFIUCCki4Iw3R4CFhSWlnSQUJW4tSUkbFKSSB8B/GD/xAAsEQABAwEGBgEEAwAAAAAAAAABAAIDEQQSEyFAURAUMDFBUFIgIkJgYWJw/9oACAECAQE/AP2XJEoZ+nispeK1XJk+VLHcNPQNBJQszyjZi0KlD9Acd1fO6qTqgwlXDsrpHf6ASFff4Kvu3VfQRTYaNtJ8KWbEQrohXTdkDoo3NHcISw/FPfGRkNe1tSgf4RFRX08Trhqjav6qWa8O2qCjcAarmmfFc23bRZ7KN901XOHZSWm+KU0IQWaz0LI3kVAWDLsnsulA8KhMjc7suXk2ToXtzKGXoGSlqx3eSnOqhxY9zVjybp0z3ZFDPqgcCNPms+vE9re4WLD8VM9hGQp0HyBqnka6hBTZWPyHTz4VGgCvImvQfGH91NE1lAEyFjaEdOO7X7kOV8qUwU+zV0/dKaINJ7BXDsi0jQRsvGlULJX8lJCGDuuyYQDmFix/FCRlw5LzoIrSYxRC2EeFLLiGuhz341KBKJ6IHA5engnDAham7KZwc6o1LaFYMPzWFD8+rU/7B//EACsRAAEDAgQFBAIDAAAAAAAAAAEAAgMRIQQSMUATIDBQUQUQFEFSYEJwcf/aAAgBAwEBPwD9lv2jRSYoMtRfKUUmYdgcaBHEUTcRmQNeQsBQjCAA3WYLO1B1eQiq4bUGNCHYJIc6GEp9qKHJs7bQW2r2OOiMUvlMjkGp32qcaBDTVN/3s2ilbUIQW1TIaHXdyNqF8Z/lDDO87ORmYL4g8qPD5SgFZWV+vZW2LnxhCSPymPzcjntahOxNna7TsL4gUIAmtpyOY1yEDE2BrdOsT7A7eysr9aVhOi4UvlRMkGp6GHws2JqIxWi9JwksMT2yNuVL6fiYWl0jKAdO3tfYhqaKc/hYTHSYQks+16bjXzsc9xpRYn1SbEMLHUoem/NSyPyVGJ/5btkhAoDRV/c6oHYlwC4gQIOwe8NXyqfSjlLvZ4cRYrgv8psbgUOiOaikgzFHC1+1FFk2NAqD2oFQKl+iSqhA9nmjLijA5QtLRuXFcWb8UJZvx6lKq39wf//Z" alt="" data-filename="2 (1).JPG" />

3.随机从这k个近邻中选出一个样本（用绿色圈出来了）。

aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAkGBwgHBgkIBwgKCgkLDRYPDQwMDRsUFRAWIB0iIiAdHx8kKDQsJCYxJx8fLT0tMTU3Ojo6Iys/RD84QzQ5Ojf/2wBDAQoKCg0MDRoPDxo3JR8lNzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzc3Nzf/wgARCADZAS8DAREAAhEBAxEB/8QAGwABAAIDAQEAAAAAAAAAAAAAAAEGAwQFAgf/xAAaAQEBAQEBAQEAAAAAAAAAAAAAAQIDBAUG/9oADAMBAAIQAxAAAAD7iAAAAAAAAgSrCgAAAAAAAAAAAAAAADmXJNlrazVAAAAAAAAAAAABCyASoApXq83jfPv+b0djl1mgAAAAAAAAAAAAjT1Kf6vLBffJ6wBEAKkAAAAAAAAACKb6PLyfRx63DvcvP6QAAAAAAABESRUgAAAAAAiQpJtAAAAAAAAFe6ceH6OG5z6XDzemaAAAAAAAAAAAAGNObc52t+UAAQkhQAAAAAAAAAAAAKz048j0cPWOl783pAAAAAAAAAAA4+sU72+Xzl9K8XslQAAB4Obc5k35sACI4vTlXvRwyZ3ePN6QAAAAABEkIqZqaAAACFAARHP3jEbmdbKiQAAAAAAAAAAAAAAACh+jy6e8Wfz+mw46CMq925cT0efc5dbjw9AAAAAHNud+a9gAAAAAACBp3O3LNoJEsgUAAAAKZ34anbjs8el08/pmgAB4j5z5/tfRvR8WbPSgAABAiwSoAAAAA0WcFZToZ0oAAUPz/S+UeL9PfPX8T6p6/g+4AAACOV058jry2MbsnLsAAAAAAAAACYssaUvj9W9+j5noAAAARq6msz6XozQAAAAAAAAA18yTLor1KAAAACJVgKAAAAAAAERURhk9S5tFAAAAAAAAAAAAAAADXRERmt9gUAAAAAAAAAAAABqXOCxm9Ga5ms/Ou3z9rXT6f5vcAAAEBQAAonq8el0x3vP3tPn9E6AAAAAcrWOR34Z8bsvHtEVLnw29bse+oAAA1bNS56mdyAARCki2QAAAAARk1BMqgAAAB889fiwdZYvJ6LPy7SAAAAAAAAADSZ5nbnGVg59ZUAAAAaDOtqdHNzLKgAAAAAAAADSZ5nbnGVg59ZUAAAAAAAAAAAAAAAARk1BMqgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB/8QAQhAAAQMCAwMIBwQHCQAAAAAAAQIDBAURAAYSEzFBFBYhMECRlNIVUFFSVFVhIDKS4gcQFyJkcaUjNVNlcHSTldH/2gAIAQEAAT8A9bOVulNuKadqUNC0EhSFvpBBG8EE49PUf5rB8QjESXGmtlyHIafbBsVtLChf2XB7YOolZKeflvvipIQHnluaTG94k2vqGOYj/wA1b8KfPjLlHVRYjzC3w+XHi5qCNO8AWtc+ztgxUo3LafKiatBfZW3q321AjH7PP49jwX58K/R5qH94s+C/N27NU2uR6oEU0ygwWUklmKHBruq9zpPADHpXNXvVLwA8mMqTa7Jqa0VMyjGDJIL8UNDXdNrHSOBPYx6mzPmL0EqMOTod24Wbqe2YGm30O++P2hfwDHjfy4ouczVKoxB5I0jbEjWmRr3JKt2kdsUpKElSiAALkk2AGET5UkByFAK2N4W67syse1KbE/i04hTUy0rTocadaVZxtYspJ4bugg8CLg/bt23O0mXFo14jAdCnAl+6CsBqxJJAxzkzP8s/pz/mxQ6tWJWZ2EyoOyQtkpfIjLbsACUk3J4ggdozLPepdHfmsBsuNlFtoCU9KgkkgEY59VP36b+A+fBz3VEpPTTvwK8+B1KkpcQUrAKSLEEXBGEU+XGAahTghjcEPNbQpHsSdQPR9b4hwkRQtWpx1103ccWbqUeH0AHACwH28yzqhAhtuUtjbul0JUNipyybE3skg7wBjnJmj5Z/Tn/NiHX8xuzGGnqdZtbyUrPIXk2STYm5NhYdgsMWHYajJcZ2bEdIVIfVZAVfSABcqVbgB3kgYMapspLjU8PucWXG0pQfoCBqT/MlWIUhEuM3IQLBYvY9BSdxB+oNx6kzPSqz6UdnszCmLcJRZ9xJaBSASQkdAuLnD9LrjDG3XWElB+5pqT5KzwAAHSTwAxlGnz6bTVN1JzU848XANZWUhViQSeOq5P2Mz0uq1BUY0uVsA2F7QbdbWom1vug45t5o+Z/1F/y4otEr8WpsPzZ+thBOtvljrmoWIHQQB1hrMAE/25KRcF0IUUC2+6gLDvwhSVpCkkFJFwQbgjsTVPhMOl5mGw26d60tpB7wL9izlmA0+SmmlgKS8hK1qL2i6SSCncbAhNicIz+ltGlNOjBP+8/LjJ1fE+qSYKIyGmdBfTpe1BBuARuG8m/U5/zxVMtVpuHAahraLAdu8DxJHAjCT2qoxOVxihKihwELbWBfQpJuDbj07xxFxjlVRSNmumlbnvoeQGu8nUPwnFOirZ2rr6gqS8u7hSCEi3QAL8AO83PUfpIgZknGBzbMkaNZf2EkNe7bGZ4c+DM2NdkPSJZaSpl4vFwFFzcXJuBjJtGzrGzLDfrS5xgjVtQ7ODifuHgFHq63V2KNGbefbdcDjgbAaAKrkE8SBawOOfMD4Gd3I8+Kbm2JPnNQ24spC3iQFuBFrgE8FE9mec2TSnLE6RewwlBW4l7WoDT9wjGc8gHM9VROFSEbQyGbbDXuKvqMAWHVyocaY3omR2n2wbhDqAoX9tiMegaP8pg+HRhikU2O6Ho1Pisup3LbZSk94HZXnigJLbZcubGx3YbYDbrjgUSVnpB3DA9RKIQklRAA3nBW4p1IQgKaULlV8R2EMJKUXsTfpN/UUmXHioCpL7TIPQC4sJB78cpZLSXA6gtq3KSbg/yIxocdW6h4JLJFk+04QgIQEpFgkWA7dLmRoTeuW+0ygmwU6sJF/ZcnHp6jfNoPiE4Yq1NkvBqNUIrzytyG30qJ4mwBv+qvVL0TS3poaDuzKBpK9IN1BO+x3YdzAX5bsqQ1HcdWTYmT90cEp/d6AB3m5wzmaPTpBciR2nWFN3cYL4AKxuKRY9hrtQzEzWJSIXLRGBGz2UQLSRpBNjpOPSuav8y/64eTGT5lWkuzBVjJskN7LbsBrpOrVb90dbW6QxWYzbL7jrYbcDgLRAVcAjiCNxOOYsD46f3t+TFNylDgTWpbUqUtbRJAXotcgp4JBwP1TKNNiur5EzymOpRUhAWkKRc3I6SARfcb3tiiUl9mTy2cEoWgENMg3033kndfgAOgDqZUlqKypx9QQgbye4D6knoAwawhsan4kqOz/jOoASPqbElI+qgMA39SZmzJLjV8xRyUNxFhTe0Sd5QDc2UN1zbCs71BQKVmmf8AErz4yJUHqjRll7Qdg+WUFPugAjiezT5jFOirlSllLCSNSgkqtcgDoAJ3nHO+ifFOeHc8uOeFD+Lc8M55esqEQSm02WW3mlhbToFylX/hBII4g4W3VX0lpa4zCbWU6yVKURx0pIASfqSq2I0duKwhhlIS22kJSkcAOzT4bFRiriykFTCiNSQopvYgjpBB3jHNCifCueIc82OZ9D+Ec8S55v8AV7//xAArEQABAwEFCAIDAQAAAAAAAAABAAIDEQQSMDFAEBQhIkFQUVIgMhNCYnD/2gAIAQIBAT8A7tcKuO8IimuoVQ/FlqLRSi30+qkdfNUBTWBC1/yt7/n41GwDTxNYfsjHZ/KlEYHJ2TjpYor6Nkp1UkNwVrrACqAZlHskQaTzFGGD2UjGhvKdRG0F1ELKwjNGztAzwgcFgBzX4ofZOjiANHY/FVKBKGgAVQjXskT2gUIQkj9VK4E8B8I3NGYQmg9U98RHKKYgbogrxVToYYg5Cxk/spYQwLL5mnVSzXKBqBGJwxmkoAeVU4E7Xn6p1Rmomv6nDa29wQsr06BzRU6YlZp8N44gKvu8q+dKSgK9la2nYz2ACquO8K6R02NFTRPsd796IWO6PvXQwsipzFXLP5UrWD6ocMRrruSFqkCdaHvFCNlVKz8vVMZ+MUrXBCu/MbOONzbKDEhga5tSVurPZTNAdQaZoJNFu0h6IwPGYxGkBAhEknTNJBqt5kHVGd5zPZObZw/zj//EACwRAAEDAQYFBAIDAAAAAAAAAAEAAgMRBBIhMEBBBRQxUFEQEyBSMmFgcHH/2gAIAQMBAT8A7tfar7UDXXVCqPi6zByFkHlRsu67lj9kLMftkDTSveOiEk52ULpD17JQegGjlkuBNtVdlHMXHWEqpKHZJXPAwCbLL4UTyTjqJCQMEZ3jZCdxKBqMkhXUB83k7IyS+E2STcaCgVBoSUAQhT0HYpIySjG/yomuAxPwewnovZm8pjJR1OZe0d0IADQyvLVzIaPxUUpdkYAVC4dw1lqhc8mhCxrRDLxWOaQiSNkABkcOls0d4zivhWN8ErAYBQbq3T2F8JELaO/xDpjlOdRcyE2cO0901rVWLiXKsIu1rmEL22r2xp6ALE7/AMFr2Euor7fKBB39CUZ/0mTfrQyPlrgr8yie49c0tvLlWeU2Bo3QVEYj4TI6bZV7JFM/FY5ks5B6IWk06KE4aZxuhcwwITtKGOW4A7IgU6JraaZwvBcuwoQNCGHZMVj/AFx//9k=" alt="" data-filename="3 (1).JPG" />

4.在阳性样本和被选出的这个近邻之间的连线上，随机找一点。这个点就是人工合成的新的阳性样本（绿色正号标出）。

aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBUODAsLDBkSEw8VHhsgHx4bHR0hJTApISMtJB0dKjkqLTEzNjY2ICg7Pzo0PjA1NjP/2wBDAQkJCQwLDBgODhgzIh0iMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzMzP/wgARCADRASEDAREAAhEBAxEB/8QAGwABAAIDAQEAAAAAAAAAAAAAAAEFBAYHAwL/xAAaAQEBAQEBAQEAAAAAAAAAAAAAAQMCBAUG/9oADAMBAAIQAxAAAADv4AAAAAAAAiKRNAAAAAAAAAAAAAAAACq6zGZz3kqAAAAAAAAAAAABEkUiVmh8udB9vlm87V4/Va86AAAAAAAAAAAAAVHWep+rzek737x+qaEcnUBZAAAAAAAAAAOe+vxYGuexeb07d5vRPQAAAAAAAQJEqpoAAAAACIWIVKgAAAAAACI1L0eeq3ytcNtuw3AAAAAAAAAAAAhPEr+plxmToAAkEhQAAAAAAAAAAABpu2Fbvjk4973h6gAAAAAAAAAIk1zXPUvd4/bLvpfi9wAAAGPZgXjLneZKAEK1nXKh9Hnzcdd38/oUAAAAASIiwv0oAAAAgmFACpvHlVrz16wqVAAAAAACFAAAAAAAAcz9fj8tON48XsuOO5oahthV7ZWmOu347gAAAfBW9cWvPYAAAAAAAHwmPWXKhQhBKgAAARHPfX5PjTi18/o3HHYAARBOV+f7XUfT8f0QAAAARACyVAAAAgrbz53nInWfOgAB8ueXeT7fLPH+l6l7vznVPT8QAAAAUXeVVvlYY6bDntIAAAAAAAB81MnhyS6Hl9XoPo+X9oAAAAMFPDrn1LDnsAAAAAAAAlFz5bR6ZXI6fJB9qAAAAIQswoAAAAAAES/NmjZfG0Lz/C6t6/1Wxde0AAAAAAAAAAAAAABGJZ9y1nHm5tl+e6x6f0+Y7AAAAAAAAAAAAAwXPh1z689Z7qi0y5vp4Ldt07z+0SoABEoUABEnNff4/DTLbvF7dky1AAAAAo+8qrbLOz02LHXxs0zHz3Wml/dpoAAIw+pi3m156lQBEQkkV9KAAAAACRzXUlQAAABCcs9vh89Od58Psv8AjUAAAAAAAAAldea3XI62PHYAAAACs64xkueO/u0AAAAAAAAAldea3XI62PHYAAAAAAAAAAAAAAAAIgmwoAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA//xABAEAABAwIDAwYLBgUFAAAAAAABAgMEBREABhITMUEUISJAUlUHFRYXIDAyUFGU0hBUcYGl0yNykpXiYXCRk6P/2gAIAQEAAT8A97eUdD74p/zKMDMVE75p/wAyjEaSzMjh+M8h5lV9LjZCkqsbGxHNvBHXb4uD6KPBw8hGgVlHyh+vHm6f74b+UP14oVLNHpDUFTweLZUdYRpvqUVbrnrlepXjqjvwdsGtoUHWUah0VBW64ve2PNie8Y3yP+eIXg8MSfHk8vZJYeS7ZMTSTpINr6j12u1PM7NdltwuXCIkp2WyhBxJGkE2Og8ceOc4dqqf20ft4yfNrUt6cKsZRSkN7Hbxg1v1ardFN+HvjMecTQKmmFyNp3UyHda5Gz3kjsns485p7ujfPf4Yy7nHx/U1wuRttaWS7rRI2m4gdkdrrcmQ1EjrkPrCW0C6lHgMCdUVp2jdJOy4BbwS4R/La35FQxDmtTmNq1qACilSVCykKG8EHcR6duuZ2n1GF4t5HG2rRe1OEsrcAUkjQDpI3q3DHlVm3un9Nf8AqxlSq1ibmGemZC2TSmwpwiOtsB0aQAdRO9JB6vm2tyKDTWJEUM63Hw2S8CUgFKjwI4gccecSrdul/wDUr9zEDPlTk1GIwo0/S8+hs6EEKspQBt0z6qTHalxlx30am3E6VD4j8RgQakgbJuq/wvi7HCnAP5rgfmUnEKE1CY2TVzclS1LN1LUd5UeJPp5nq1Zpi4opcPbhwL2hEZb2gi2n2CLXx5VZt7p/TX/qxRa/mKZWI0abTtlFWTrc5E63pASTvKiPX2GLdRmypHK24UTSH3E61uKFw2gG17cSSbAXw6mpU9JkiWZraOd1lbaQojiUFIHOOAN77rjDTiXmkONkFC0hSVDiCLg+46tRcwxqs9MVU9DMl5QS5y11AbTqJSFkDoixsOAOJlJzJFQm9ZK1uWDTTdReKnPwGnGXIEulUKNCnPB19kKBUFlQtclIBIB5k2G70MxUWvVGpJfps/YRw0lJRytxrpBRJNkgg3GPJXNve/6k/wDTjLdErtOqS36lP28ctKSEcqcd6RIINlAAWAI9UpaW0KWpQCQLkk2AGE16m/eCEGwS6ptQbN91lkaT/wA9SUhK0lCgCkixBFwRiNToUMqVFiMMKV7RabSkq/Gw6jmjNvJq2aW5DacZjrC1hcjSHeiFAEaTYAkHCvCSlwFCqXFKeIM3/DGSK8aq1NihkNtwyjZkO6+iu5Cb2Hs+mPsrHhBq8DwkigMtQzDMlhnWUHXZYSTxwjnT1moRFvhpyO4lEphepoqBIPAggcCDb/Tfgy6oobNFJKHe2t5BaH5g6j/SMU6HyOKEFRcdUordWRbUsm5NuA+A4AAeoz/R84z6+y7QnZbMARkpWWpmyTr1KuSnFQhVNnMfIX3H3a6JSEtvbe5cKgNBCibgjo2JOPB5SM5wK+87mEzTDMYhAfmB4a7p4BR9XXMyRaAthEhiQ8XwooDITuTa99Sh8cecOB3fP/pb+vFFzXErU4xGY0lpwNly7oQAQCAdyj2h1WQ/ydsK0KXcgWThDKhIW6XCUqAAQdwxU/BsajnoZk8bbO0hl7YbDsAD2r4Hq5VMhTykzYkeTovo2zaV6b77XHNfHk5Q+5oHyqMRaTT4LpciQYzCyLa2mkpJHwuB1OmZnpFXlGNAlbV1KSojZqTzAgcQBhby0uNpQ2VpVvWDzDEdgRwsBazqUT0je3uKvZ+VR6xJgCnB7ZW6Ze07wDuscZdrQoM92SY23DjRaKNeneRxscZSrYrtKceEbYBpwthGvXwBvew+PuGRPiRLCTKYZUr2Q44lJV+FzgvtDQC4np+xbjhdEhTH3np1OiOuK3LLYKlAbrm19wGMgQo86vPtSmGn0CMTZ1AVxGIcKLBaLcWOywgm5S0gJBO69h1yVUoUDSJsuPG130bZxKNVt9rnntgZjoffED5lGItWp09wtQ50V9wC+hp1KyB8bA/ZmavHL0BqSGUOlx0NWWvQBcKNybHs4bzAC6pyS1HddcVd10yLqX8eG74DcBijZpZj1hEKMw27DkPtoaSX7FsqICikWPNx03wMAAevn1bNjdSmIaNRDSX1hrRAChpCyBY7M3FseOc49qqf24ft4yjKqkqmvqq222ofsgvM7I6NKeGlPEq4esreXItfWwuS9IZLAUEFkp3Kte+pJ+Ax5vKb3hUf/P6MUXKkSizzLYkyXXC2W7OlG4kE7kjsj7HG0PNLbWLoWClQPEHmIw5QqpDOxZjmWyOZtaVoBCeAWFEc4+IvfFBozsJbsuXpMl0BIQjc2gG9r8STzk+pmTmYLQW+ojUoJQlKSpS1HcABzk4brDYeQ3IjvxdoqyFPBOlZO4XSSATwBsT7kqOc57OY5HPBHJFuMtBaCbDWUknpjnIGJWeqhMiusPGmFtwFJAQv68ZUqUir5biTZOnbL1A6R2VFN953gdUGKlVoVHYS9MeLTa1hAIQpZKrE2sATuBx5b0D7478q79OGc40N99plqYsuOrShF47gBUo2AuU2HrJ8FT7rb8dzYy2b6FEXStJ3oUOINgebnBAOHYdQnpMeYY7EZXM6GFqUp0cRcpGkHjvNuIwlISNKRYDqgxU6VCrDCGZrJdbQsLAC1IIVYi9wQdxOPIigfc3fmnfqwzk6hx32nmoaw40tK0XkOEBSTcGxVY/7Zf/EACsRAAEDAgQFBAMBAQAAAAAAAAEAAgMRMQQhMEAQEhNBURRCUFIgIjJhcP/aAAgBAgEBPwDY14UHwYYT2XIfCIO8y4U/xDjZNxpaLI44kWTzzGu8Y8g1ohjKe1S4svFOVX4kLJZbeFkNP3K6eH8qZrB/CGWyJoiadkNYcM9lZQw9Tuhgq+5Sw9Pvum2TW1KoPKI+DgaCTVdGH7KZkYGR2wzUMYcaFehb9k/CtaCa6dQifziaw3K6MH2UjGAZGusKoHaAAI7CuyjkiAzautD9E51TVDjE+Mf0KrrQfVPc11hp0+DuoYQ8XTcEfspmch/MFZJ8rhJyhd9OgCuqAagJQDR3RNdCZr/aUecSZ3ULZQ6r9NkRevSPCfhyzM7UlAJ8VXhyFtMOIXUPlFxOza6qLkG7CmyfJyKNyZb4Imi5A66hZnvWgu7LpO8ItcOETA80UmBDvcvTFjSebYXuoGYcj9yjFhRYqUNB/TUjlcywRxUhTpjJdUQJT4XO9yYKC6A0aflRZIU1q6oUUDXtzKGFYBWqkaA6g2hTG1svTTeEYJAKkagJQJVSTtCmOpZepm8ozyEUJ+Dp/wAP/8QALBEAAQMBBgYCAQUAAAAAAAAAAQACAxEEITAxQEEFEhMUIFEQUEIiI1JhcP/aAAgBAwEBPwD7YvAQeDuga60Ee0CD4G9PsYduhYgN0xvKKax7A4Zo2QndRwFqA8L1fp5Hy1uXUnUT3HPRgaAooU0QUkpYu6/pRzc2qKJoECaJp86BU1c7iMl1paZKJ8jjeNNkpZC0XLu3eky0uO2GGoDzeXjJdWUbKJ7jnjGioPSFPWhqqq/4u+hfHKcnJsU38kwUR+XskORQhl9qNhGeGHaOnjRUw5ZnNKNrB/FRP5sGHhrH2Ezk3ogC4YlMUtaqk/imjzzK4bNY4weuKqGSzGzF4H7a4nNYntHbihw3ycq7oJkwdo6AK75h4o6Oymz8txRywy0FdMIMpo4rXBKaNKJOw8Kb1w6aPehVr4r0JDGG1VjtnQkLiK1VitRtDOalPoaoGpqE+BrnFxauFRc0rgWqNgY2gFNYS0boSNO6a8O+JZAwZIz1OShkKBQAGNlkpHzg/pXPOVFzkX4j4mPzQs0YTIuT4IqKUToiNlHGGquCHed6KFcWmKVJM9pXcPdsoiSL9IE51F3EXtCeM74ha1crU0AaQJzart4vSEEY2/zL/9k=" alt="" data-filename="4 (1).JPG" />

以上来自http://sofasofa.io/forum_main_post.php?postid=1000817中的叙述

(2).

With this approach, the positive class is over-sampled by taking each minority class sample and introducing synthetic examples along the line segments joining any/all of the k minority class nearest neighbours. Depending upon the amount of over-sampling required, neighbours from the k nearest neighbours are randomly chosen. This process is illustrated in the following Figure, where xixi is the selected point, xi1xi1 to xi4xi4are some selected nearest neighbours and r1r1 to r4r4 the synthetic data points created by the randomized interpolation. The implementation of this work uses only one nearest neighbour with the euclidean distance, and balances both classes to 50% distribution.

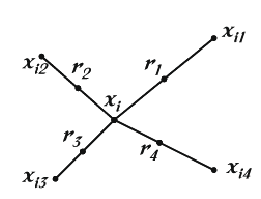
Synthetic samples are generated in the following way: Take the difference between the feature vector (sample) under consideration and its nearest neighbour. Multiply this difference by a random number between 0 and 1, and add it to the feature vector under consideration. This causes the selection of a random point along the line segment between two specific features. This approach effectively forces the decision region of the minority class to become more general. An example is detailed in the next Figure.

In short, the main idea is to form new minority class examples by interpolating between several minority class examples that lie together. In contrast with the common replication techniques (for example random oversampling), in which the decision region usually become more specific, with SMOTE the overfitting problem is somehow avoided by causing the decision boundaries for the minority class to be larger and to spread further into the majority class space, since it provides related minority class samples to learn from. Specifically, selecting a small k-value could also avoid the risk of including some noise in the data.

以上来自https://sci2s.ugr.es/multi-imbalanced中的叙述

二.spark实现smote

核心代码如下，完整代码https://github.com/jiangnanboy/spark-smote/blob/master/spark%20smote.txt

 /**
      *  (1) 对于少数类(X)中每一个样本x，计算它到少数类样本集(X)中所有样本的距离，得到其k近邻。
      *  (2) 根据样本不平衡比例设置一个采样比例以确定采样倍率sampling_rate，对于每一个少数类样本x，
      *      从其k近邻中随机选择sampling_rate个近邻，假设选择的近邻为 x(1),x(2),...,x(sampling_rate)。
      *  (3) 对于每一个随机选出的近邻 x(i)(i=1,2,...,sampling_rate)，分别与原样本按照如下的公式构建新的样本
      *      xnew=x+rand(0,1)?(x(i)?x)
      *
      *  http://sofasofa.io/forum_main_post.php?postid=1000817
      *  http://sci2s.ugr.es/multi-imbalanced
      * @param session
      * @param labelFeatures
      * @param knn 样本相似近邻
      * @param samplingRate 近邻采样率 (knn * samplingRate),从knn中选择几个近邻
      * @parm rationToMax 采样比率(与最多类样本数的比率) 0.1表示与最多样本的比率是 -> (1:10),即达到最多样本的比率
      * @return
      */
     public static Dataset<Row> smote(SparkSession session, Dataset<Row> labelFeatures, int knn, double samplingRate, double rationToMax) {

         Dataset<Row> labelCountDataset = labelFeatures.groupBy("label").agg(count("label").as("keyCount"));
         List<Row> listRow = labelCountDataset.collectAsList();
         ConcurrentMap<String, Long> keyCountConMap = new ConcurrentHashMap<>(); //每个label对应的样本数
         for(Row row : listRow)
             keyCountConMap.put(row.getString(0), row.getLong(1));
         Row maxSizeRow = labelCountDataset.select(max("keyCount").as("maxSize")).first();
         long maxSize = maxSizeRow.getAs("maxSize");//最大样本数

         JavaPairRDD<String, SparseVector> sparseVectorJPR = labelFeatures.toJavaRDD().mapToPair(row -> {
             String label = row.getString(0);
             SparseVector features = (SparseVector) row.get(1);
             return new Tuple2<String, SparseVector>(label, features);
         });

         JavaPairRDD<String, List<SparseVector>> combineByKeyPairRDD = sparseVectorJPR.combineByKey(sparseVector -> {
                     List<SparseVector> list = new ArrayList<>();
                     list.add(sparseVector);
                     return list;
                 }, (list, sparseVector) -> {list.add(sparseVector);return list;},
                 (list_A, list_B) -> {list_A.addAll(list_B);return list_A;});

         JavaSparkContext jsc = JavaSparkContext.fromSparkContext(session.sparkContext());
         final Broadcast<ConcurrentMap<String, Long>> keyCountBroadcast = jsc.broadcast(keyCountConMap);
         final Broadcast<Long> maxSizeBroadcast = jsc.broadcast(maxSize);
         final Broadcast<Integer> knnBroadcast = jsc.broadcast(knn);
         final Broadcast<Double> samplingRateBroadcast = jsc.broadcast(samplingRate);
         final Broadcast<Double> rationToMaxBroadcast = jsc.broadcast(rationToMax);

         /**
          * JavaPairRDD<String, List<SparseVector>>
          * JavaPairRDD<String, String>
          * JavaRDD<Row>
          */
         JavaPairRDD<String, List<SparseVector>> pairRDD = combineByKeyPairRDD
                 .filter(slt -> {
                     return slt._2().size() > 1;
                 })
                 .mapToPair(slt -> {
                     String label = slt._1();
                     ConcurrentMap<String, Long> keySizeConMap = keyCountBroadcast.getValue();
                     long oldSampleSize = keySizeConMap.get(label);
                     long max = maxSizeBroadcast.getValue();
                     double ration = rationToMaxBroadcast.getValue();
                     int Knn = knnBroadcast.getValue();
                     double rate = samplingRateBroadcast.getValue();
                     if (oldSampleSize < maxSize * rationToMax) {
                         int needSampleSize = (int) (max * ration - oldSampleSize);
                         List<SparseVector> list = generateSample(slt._2(), needSampleSize, Knn, rate);
                         return new Tuple2<String, List<SparseVector>>(label, list);
                     } else {
                         return slt;
                     }
                 });

         JavaRDD<Row> javaRowRDD = pairRDD.flatMapToPair(slt -> {
             List<Tuple2<String, SparseVector>> floatPairList = new ArrayList<>();
             String label = slt._1();
             for(SparseVector sv : slt._2())
                 floatPairList.add(new Tuple2<String, SparseVector>(label, sv));
             return floatPairList.iterator();
         }).map(svt->{
             return RowFactory.create(svt._1(), svt._2());
         });

         Dataset<Row> resultDataset = session.createDataset(javaRowRDD.rdd(), EncoderInit.getlabelFeaturesRowEncoder());
         return resultDataset;
     }