[NOIP2018]:旅行（数据加强版）（基环树+搜索+乱搞）

题目描述

小$Y$是一个爱好旅行的$OIer$。她来到$X$国，打算将各个城市都玩一遍。
小$Y$了解到，$X$国的$n$个城市之间有$m$条双向道路。每条双向道路连接两个城市。不存在两条连接同一对城市的道路，也不存在一条连接一个城市和它本身的道路。并且，从任意一个城市出发，通过这些道路都可以到达任意一个其他城市。小$Y$只能通过这些道路从一个城市前往另一个城市。
小$Y$的旅行方案是这样的：任意选定一个城市作为起点，然后从起点开始，每次可以选择一条与当前城市相连的道路，走向一个没有去过的城市，或者沿着第一次访问该城市时经过的道路后退到上一个城市。当小$Y$回到起点时，她可以选择结束这次旅行或继续旅行。需要注意的是，小$Y$要求在旅行方案中，每个城市都被访问到。
为了让自己的旅行更有意义，小$Y$决定在每到达一个新的城市（包括起点）时，将它的编号记录下来。她知道这样会形成一个长度为$n$的序列。她希望这个序列的字典序最小，你能帮帮她吗？
对于两个长度均为$n$的序列$A$和$B$，当且仅当存在一个正整数$x$，满足以下条件时，我们说序列$A$的字典序小于$B$。
　　$\bullet$对于任意正整数$1\leqslant i\leqslant x$，序列$A$的第$i$个元素$A_i$和序列$B$的第$i$个元素$B_i$相同。
　　$\bullet$序列$A$的第$x$个元素的值小于序列$B$的第$x$个元素的值。

---

输入格式

输入文件名为$travel.in$。
输入文件共$m+1$行。第一行包含两个整数$n,m$中间用一个空格分隔。
接下来$m$行，每行包含两个整数$u,v$，表示编号为$u$和$v$的城市之间有一条道路，两个整数之间用一个空格分隔。

---

输出格式

输出文件名为$travel.out$。
输出文件包含一行，$n$个整数，表示字典序最小的序列。相邻两个整数之间用一个空格分隔。

---

样例

样例输入1：

6 5
1 3
2 3
2 5
3 4
4 6

样例输出1：

1 3 2 5 4 6

样例输入2：

6 6
1 3
2 3
2 5
3 4
4 5
4 6

样例输出2：

1 3 2 4 5 6

---

数据范围与提示

对于全部测试数据，$1\leqslant n\leqslant 5\times 10^3$，且$m=n-1$或$m=n$。保证$1\leqslant u,v\leqslant n$。
对于不同的测试点，我们约定数据的规模如下：

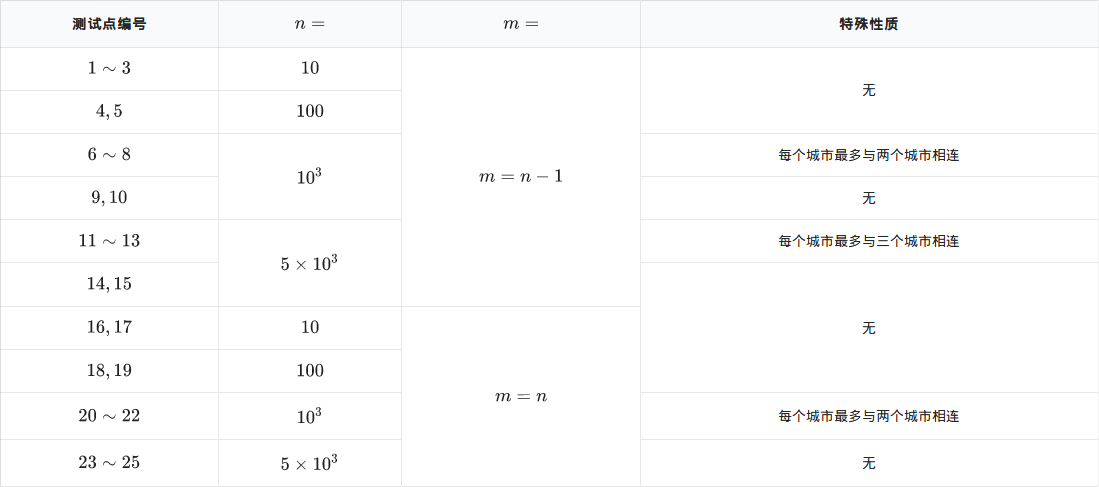
加强版数据范围：

对于$100\%$的数据和所有样例，$1\leqslant n\leqslant 500000$且$m=n-1$或$m=n$。
具体规定详见正常版本（除$testcase11-13$）

---

题解

$\Theta(n^2)$暴力不再赘述，找到环枚举断点即可。

考虑乱搞。

用$clock()$，防止超时。

发现$WA80$了。

$reverse$

时间复杂度：$\Theta(n^2)$。

期望得分：$70$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,m;
bool vis[500001];
int dfn[500001],fa[500001],sta[500001],vec[500001],ans[500001],top,tim,cnt;
vector<int>e[500001];
void dfs(int x)
{
	vis[x]=1;printf("%d ",x);
	int t=e[x].size();
	for(int i=0;i<t;i++)
		if(!vis[e[x][i]])dfs(e[x][i]);
}
void tarjan(int x)
{
	dfn[x]=++tim;
	sta[++top]=x;
	int t=e[x].size();
	for(int i=0;i<t;i++)
	{
		if(dfn[e[x][i]])
		{
			if(dfn[e[x][i]]<dfn[x])continue;
			int y=e[x][i];
			vec[++cnt]=y;
			while(y!=x)
			{
				y=fa[y];
				vec[++cnt]=y;
			}
		}
		else
		{
			fa[e[x][i]]=x;
			tarjan(e[x][i]);
		}
	}
}
void dfs(int x,int l,int r)
{
	vis[x]=1;sta[++top]=x;
	int t=e[x].size();
	for(int i=0;i<t;i++)
	{
		if((x==l&&e[x][i]==r)||(x==r&&e[x][i]==l))continue;
		if(!vis[e[x][i]])dfs(e[x][i],l,r);
	}
}
bool judge()
{
	for(int i=1;i<=top;i++)
	{
		if(ans[i]>sta[i])return 1;
		if(ans[i]<sta[i])return 0;
	}
	return 0;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		e[u].push_back(v);
		e[v].push_back(u);
	}
	for(int i=1;i<=n;i++)sort(e[i].begin(),e[i].end());
	if(m==n-1)dfs(1);
	else
	{
		tarjan(1);top=0;
		reverse(vec+1,vec+cnt+1);
		dfs(1,vec[1],vec[cnt]);
		memcpy(ans,sta,sizeof(sta));
		for(int i=1;i<cnt;i++)
		{
			memset(vis,0,sizeof(vis));
			top=0;dfs(1,vec[i],vec[i+1]);
			if(judge())memcpy(ans,sta,sizeof(sta));
			if(clock()>910000)break;
		}
		for(int i=1;i<=top;i++)printf("%d ",ans[i]);
	}
	return 0;
}

---

rp++