南大《软件分析》课程笔记——Data Flow Analysis

南大《软件分析》——Data Flow Analysis

@(静态分析)

目录

1. 数据流分析概述

2. 数据流分析应用

• Reaching Definitions Analysis(may analysis)
• Live Variables Analysis(may analysis)
• Available Expressions Analysis(must analysis)

数据流分析

相关概念

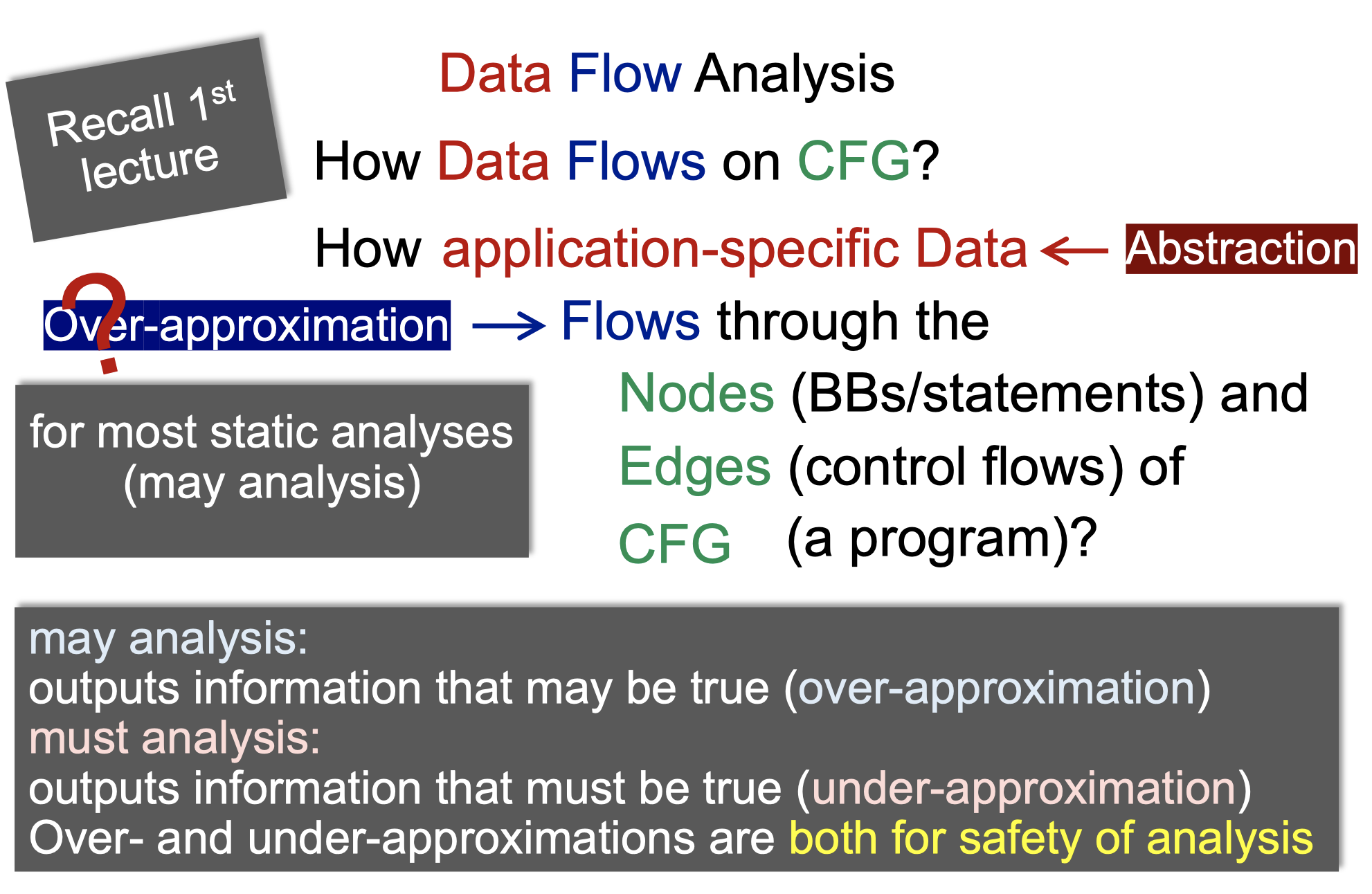
may analysis: 输出可能是正确的，要做over-approxiamation追求sound，可以有误报

must analysis: 输出必须是正确的，要做under-approxiamation追求complete，可以有漏报

无论是over还是under-approxiamation，目标都是实现safe-approxiamation

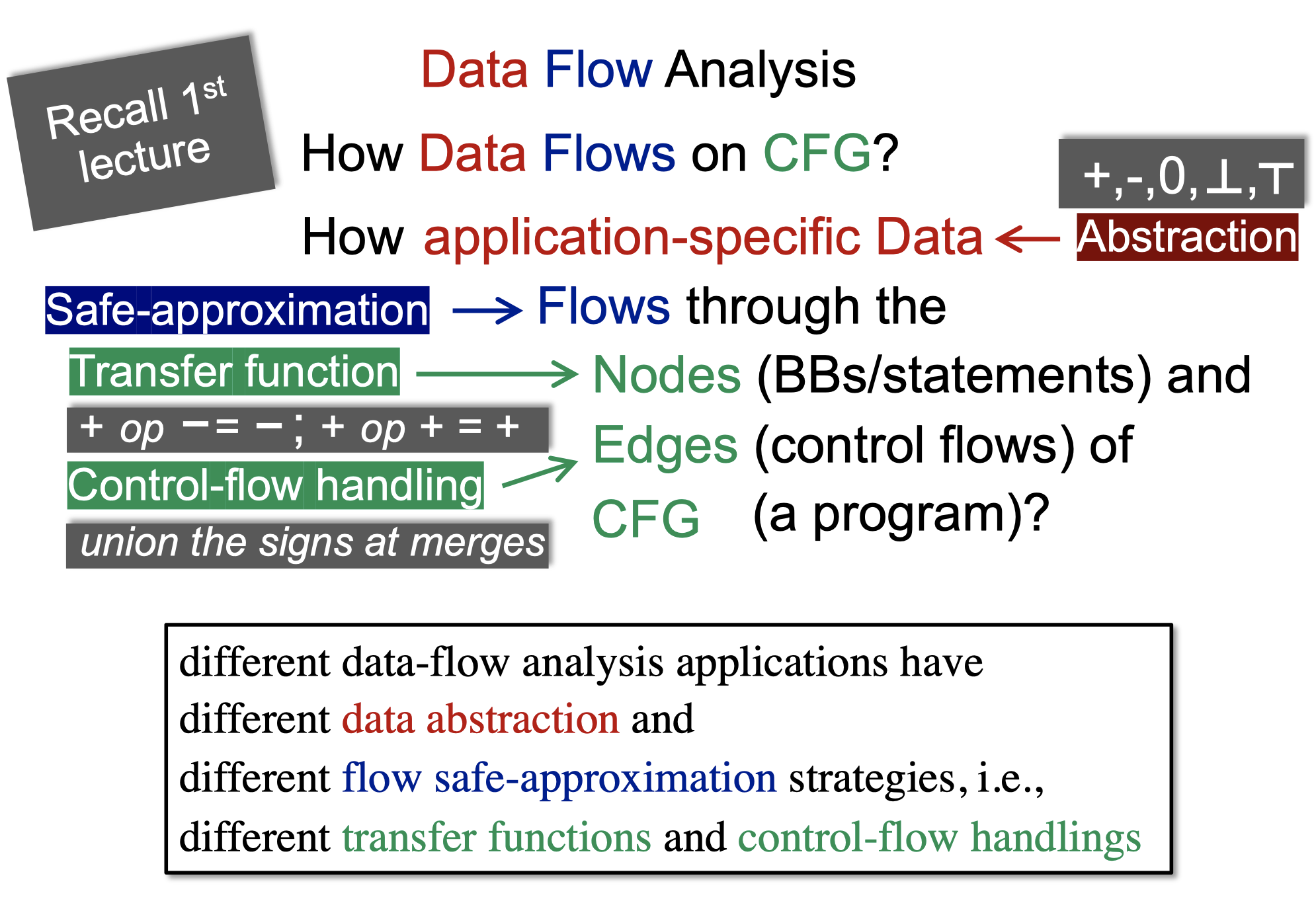
不同的数据流分析会有不同的数据抽象表达， 不同的安全近似策略，即转换函数和控制流处理。

前置知识

Input and Output States

Input and Output States(输入输出状态)：程序执行前和执行后的状态

• IR语句的每次执行都会从输入状态转换到新的输出状态。
• 输入（输出）状态与语句之前（之后）的程序点相关联。
  
  

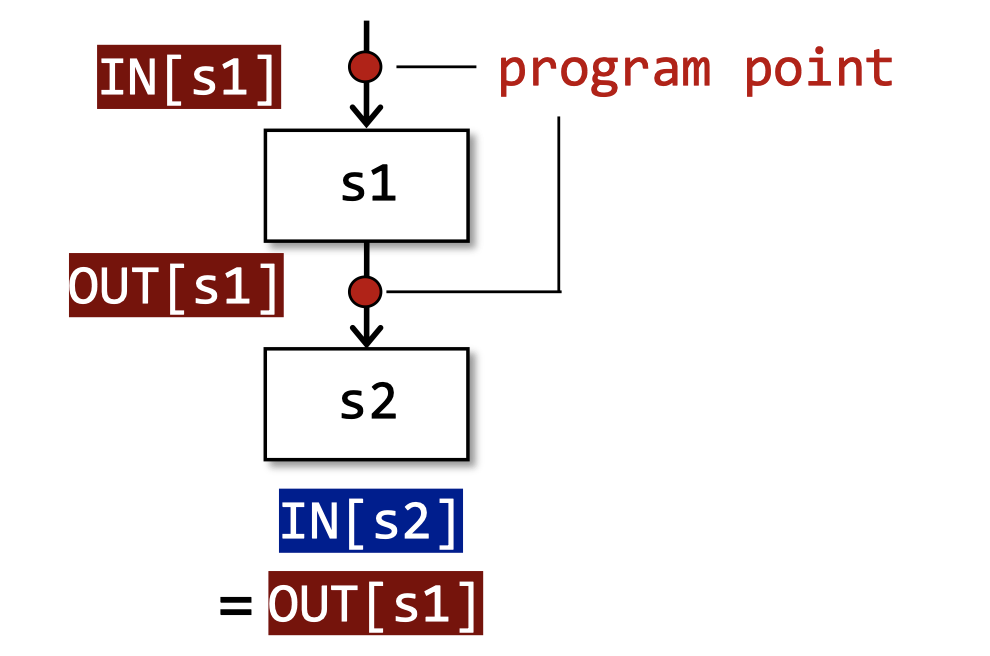
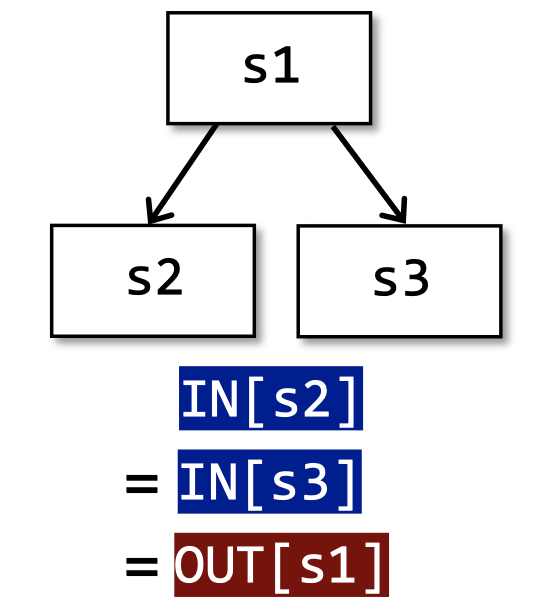
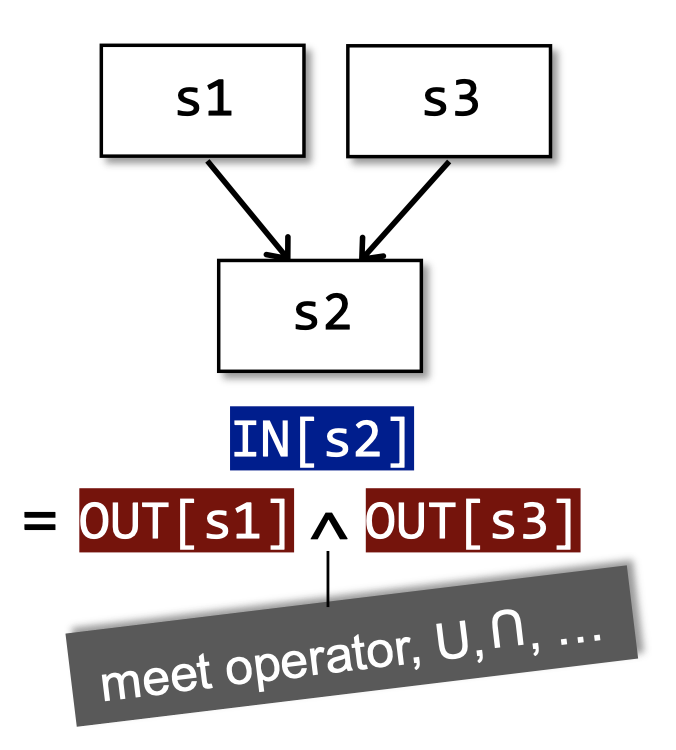
以上是三种控制流：顺序执行、分支、汇聚

数据流分析结果

In each data-flow analysis application, we associate with every program point a data-flow value that represents an abstraction of the set of all possible program states that can be observed for that point.

在每个数据流分析应用程序中，我们与每个程序点关联一个数据流值，该值代表对该点可以观察到的所有可能程序状态集的抽象。

结果的集合如下，我们只需要该程序点的抽象值

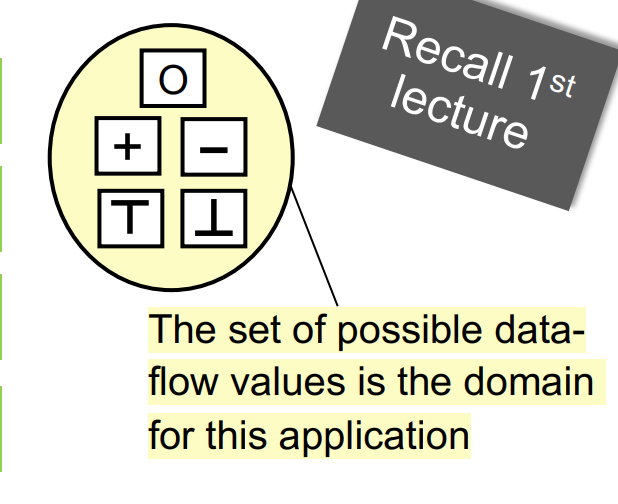
Data-flow analysis is to find a solution to a set of safe-approximation directed constraints on the IN[s]’s and OUT[s]’s, for all statements s.

• constraints based on semantics of statements (transfer functions)
• constraints based on the flows of control

Notations for Transfer Function’s Constraints

Transfer Funciton: 给一个input按预定规则输出一个output

转换函数约束分析

• 前向分析
  
  

• 反向分析
  
  

Notations for Control Flow’s Constraints

控制流约束分析

• Basic Block内部的
• Basic Block之间的（分为前向和反向）
  
  

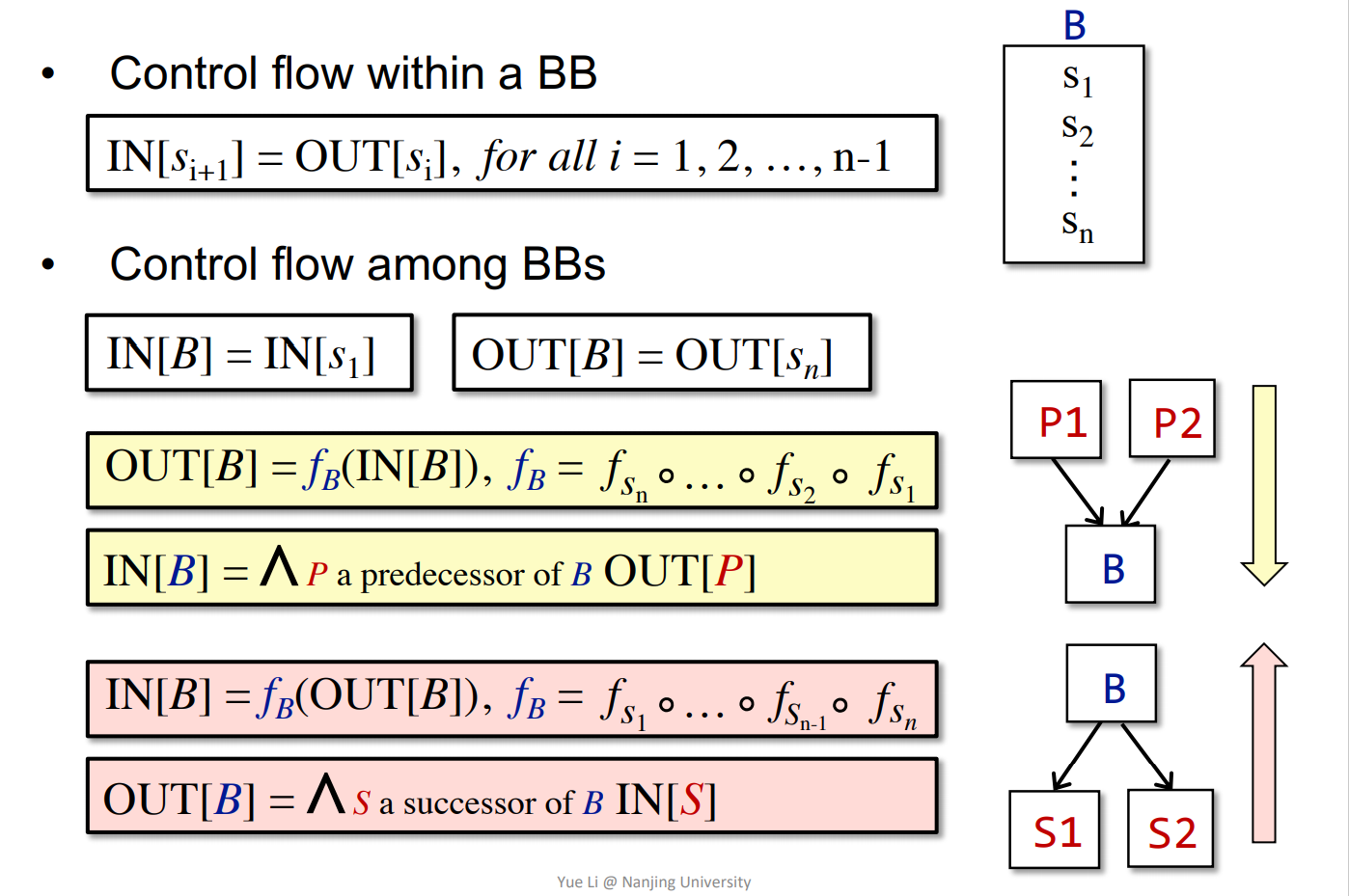
数据流分析方法

Reaching Definitions Analysis(到达定值分析)

定义：给变量v一个定义d（赋值过程），从程序点p到q存在一个完整路径，且v的定义未被改变

A definition d at program point p reaches a point q if there is a path

from p to q such that d is not “killed” along that path

应用：检测变量是否被初始化。例如，在CFG的入口给每个变量v引入一个虚拟定义，如果这个虚拟定义到达了程序点p即变量v被使用的地方，这就说明v可能未被定义，即未初始化。

Reaching definitions can be used to detect possible undefined

variables. e.g., introduce a dummy definition for each variable v at

the entry of CFG, and if the dummy definition of v reaches a point

p where v is used, then v may be used before definition (as

undefined reaches v)

公式分析

$$ D: v = x\ op\ y $$

该语句“生成”变量v的定义D，并“杀死”程序中定义变量v的所有其他定义，而其余输入定义不受影响。

This statement “generates” a definition D of variable v and “kills” all the other definitions in the program that define variable v, while leaving the remaining incoming definitions unaffected.

Transfer Funtion

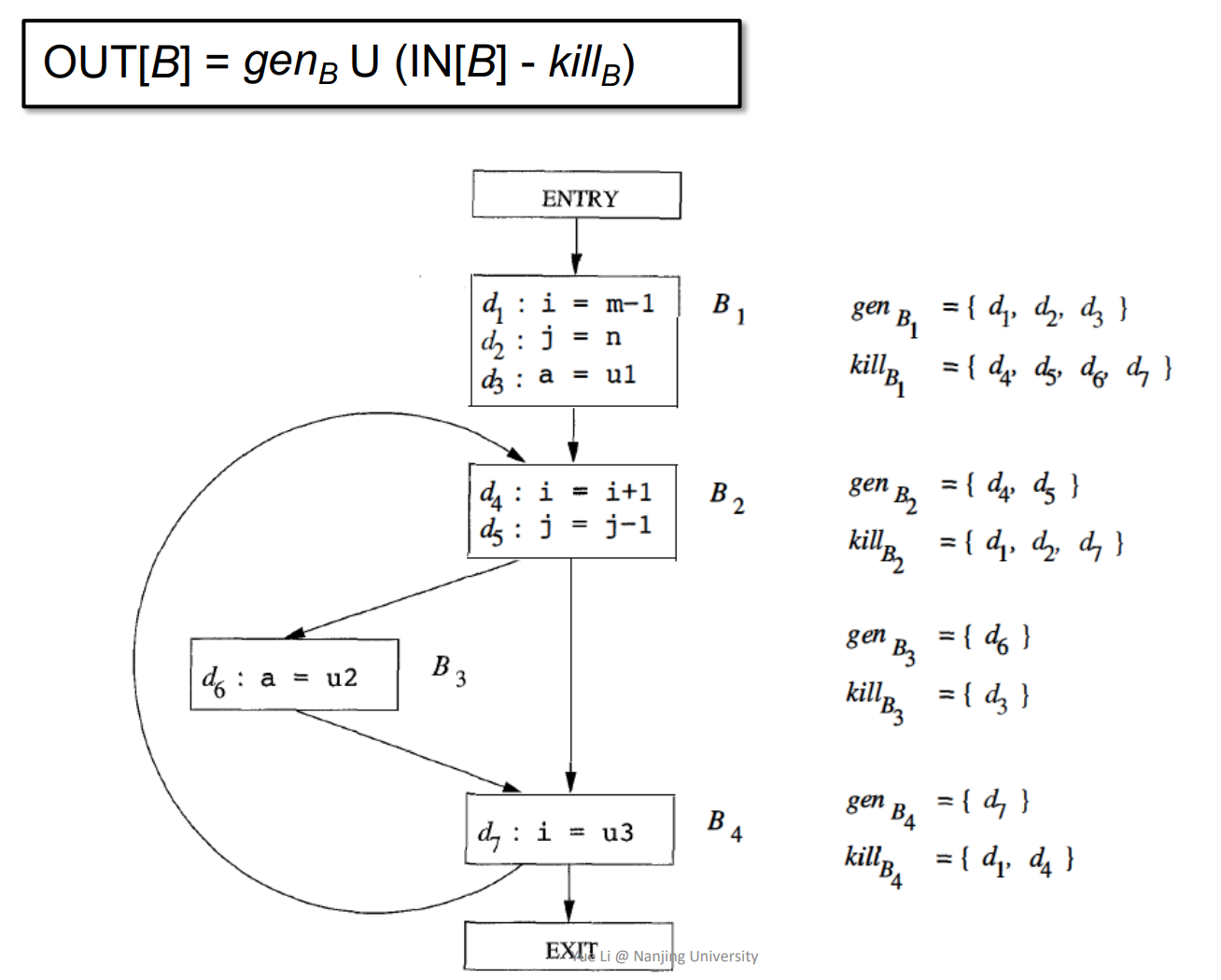
基本块的输出等于这个基本块中的定义与此基本块的输入减去程序中其它所有定义了变量v的语句的并集。

本质上输出的就是此基本块与前驱中所有修改变量语句的和

Control Flow

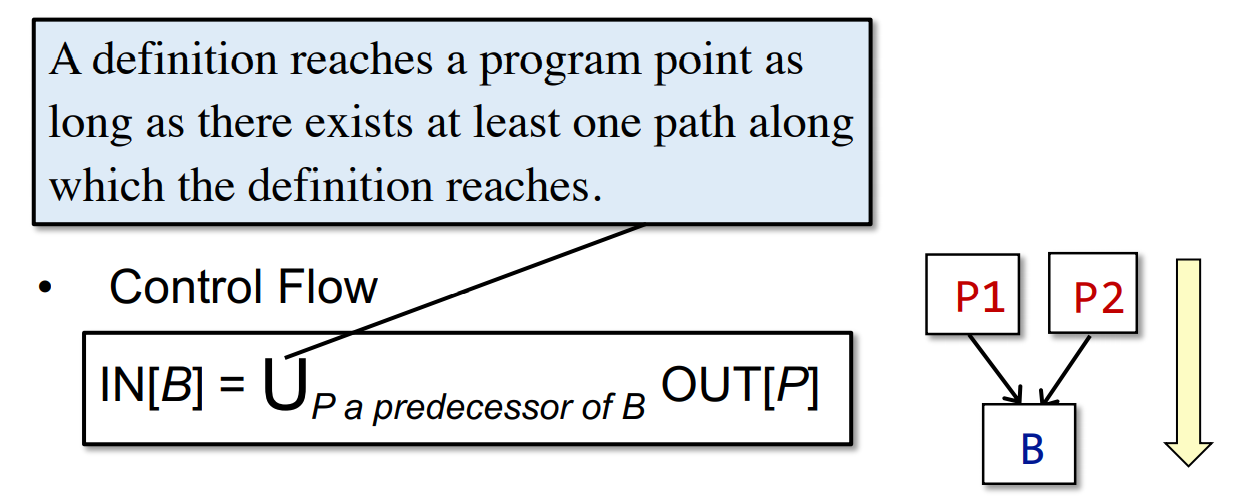
基本块B的输入 = 块B所有前驱块P的输出的并集。注意，所有前驱块意味着只要有一条路径能够到达块B，就是它的前驱，包括条件跳转与无条件跳转。

算法

Iterative algorithm

目的：输入CFG(计算好每个基本块的$kill_B$和$gen_B$)，输出每个基本块的$IN[B]$和$OUT[B]$

算法过程：

boundary condition:初始化OUT[entry]为空

然后所有基本块的OUT[B]初始化为空。（不同的分析方法不一样，may analysis一般初始化为空，must analysis一般初始化为TOP）

遍历每一个基本块B，按Transfer function和Control flow的约束求解块B的IN[B]和OUT[B]，只要这次遍历时有某个块的OUT[B]发生变化，则重新遍历一次（因为程序中有循环存在，只要某块的OUT[B]变了，就意味着后继块的IN[B]变了）。

例子

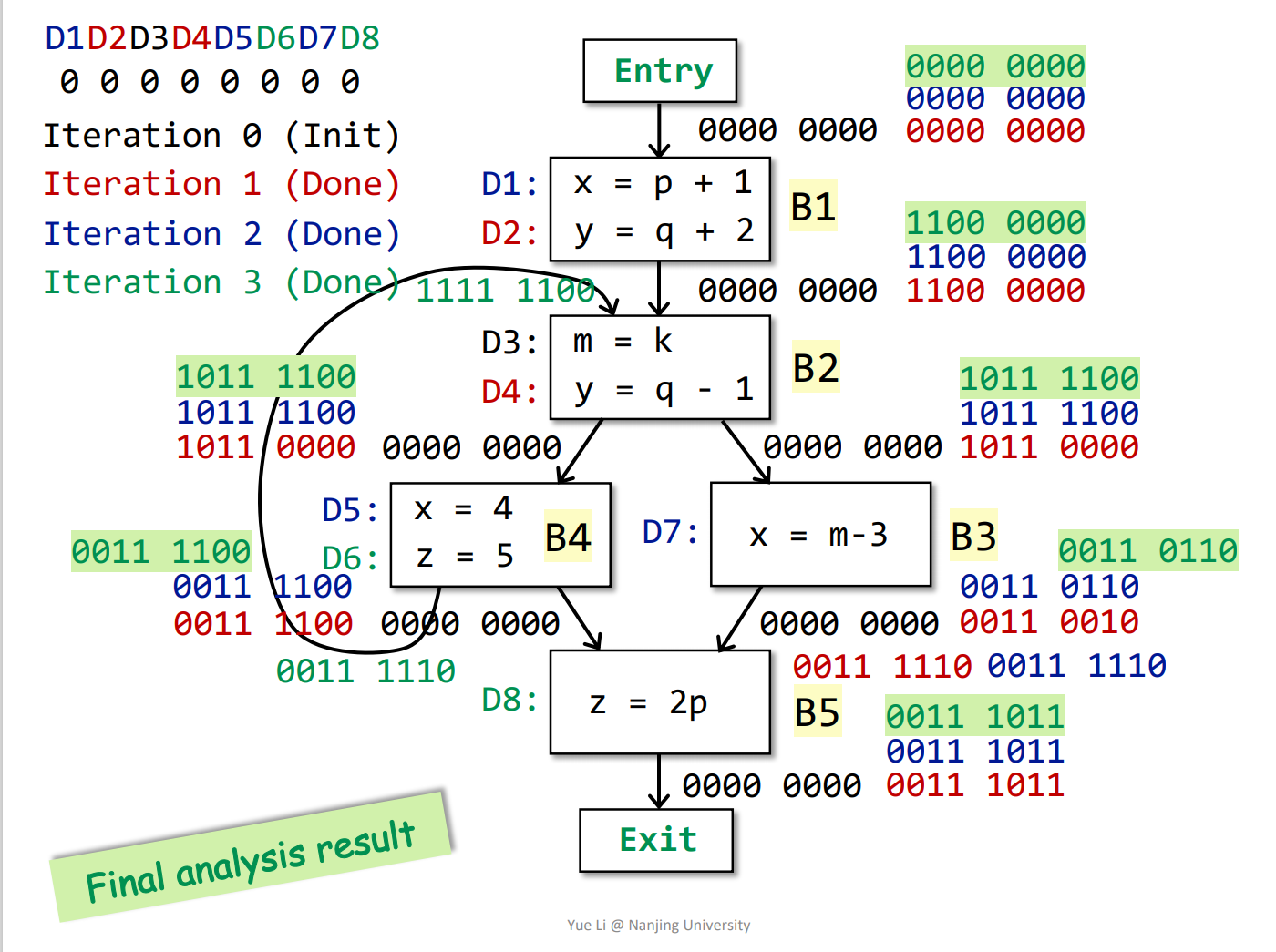
抽象表示：设程序有n条赋值语句，用n位向量来表示能reach与不能reach。

说明：红色-第1次遍历；蓝色-第2次遍历；绿色-第3次遍历。

结果：3次遍历之后，每个基本块的OUT[B]都不再变化，遍历停止。

在经过数据流分析算法过后，每个程序点都关联了一个数据流值，该值代表对该点可以观察到的所有可能程序状态的集合的抽象表示（即图里的位向量）

不停用约束求解，最终得到一个稳定的安全的近似约束集。

为什么迭代会停止？

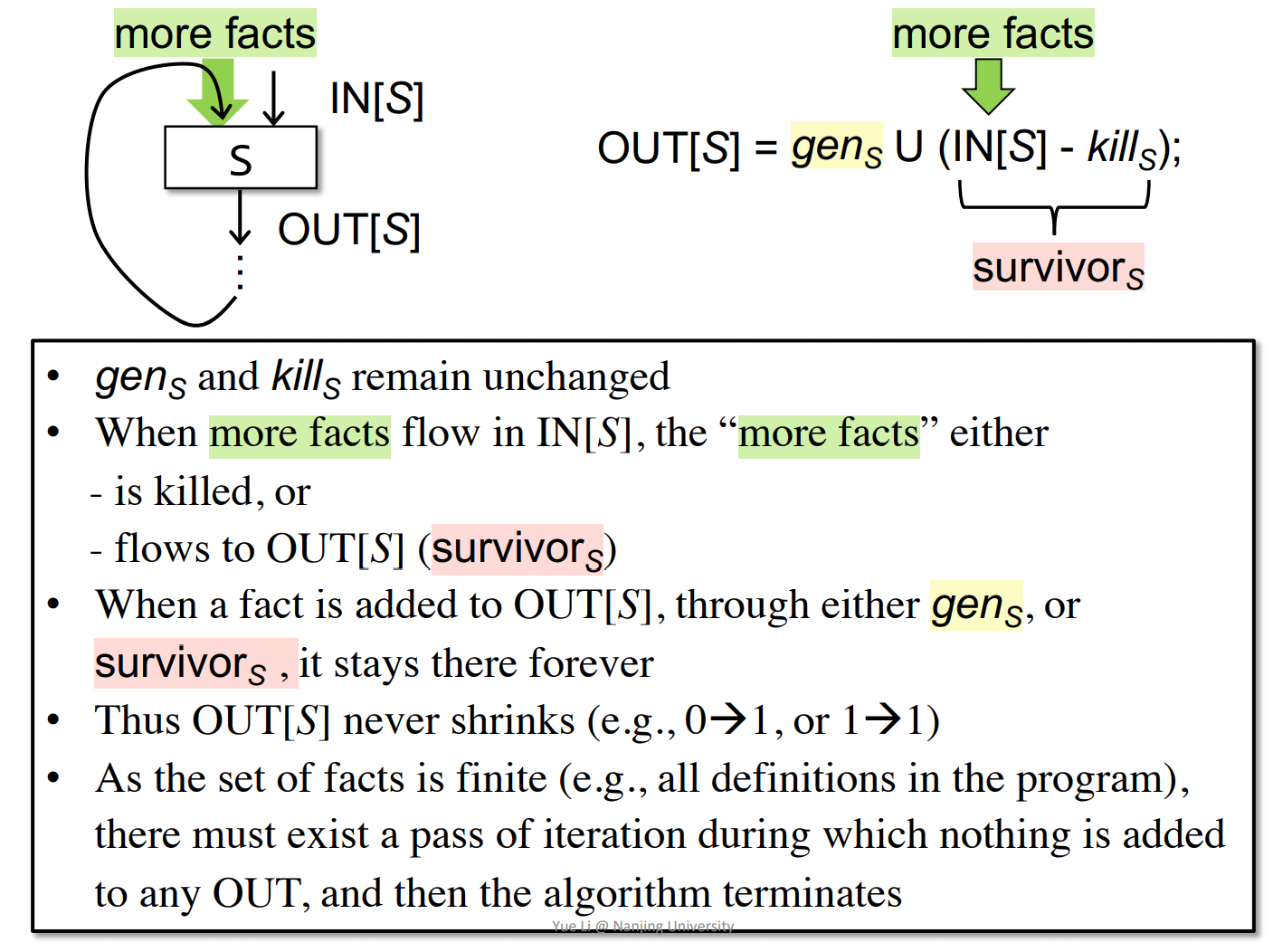
$gen_B$和$kill_B$是不变的，只有IN[B]在变化，所以说OUT[B]只会增加不会减少，n向量长度是有限的，所以最终肯定会停止。

迭代停止说明到达了不动点(fixed point)。

Live Variables Analysis(活跃变量分析)

Live variables analysis tells whether the value of variable v at

program point p could be used along some path in CFG starting at p.

If so, v is live at p; otherwise, v is dead at p.

某程序点p处的变量v，从p开始到exit块的CFG中是否有某条路径用到了v，如果用到了v，则v在p点为live，否则为dead。其中有一个隐含条件，在点p和引用点之间不能重定义v。

（感觉跟污点分析有点类似，标记污点如果路径中用到了就作污点传播，重定义了就消除污点）

用backword analysis

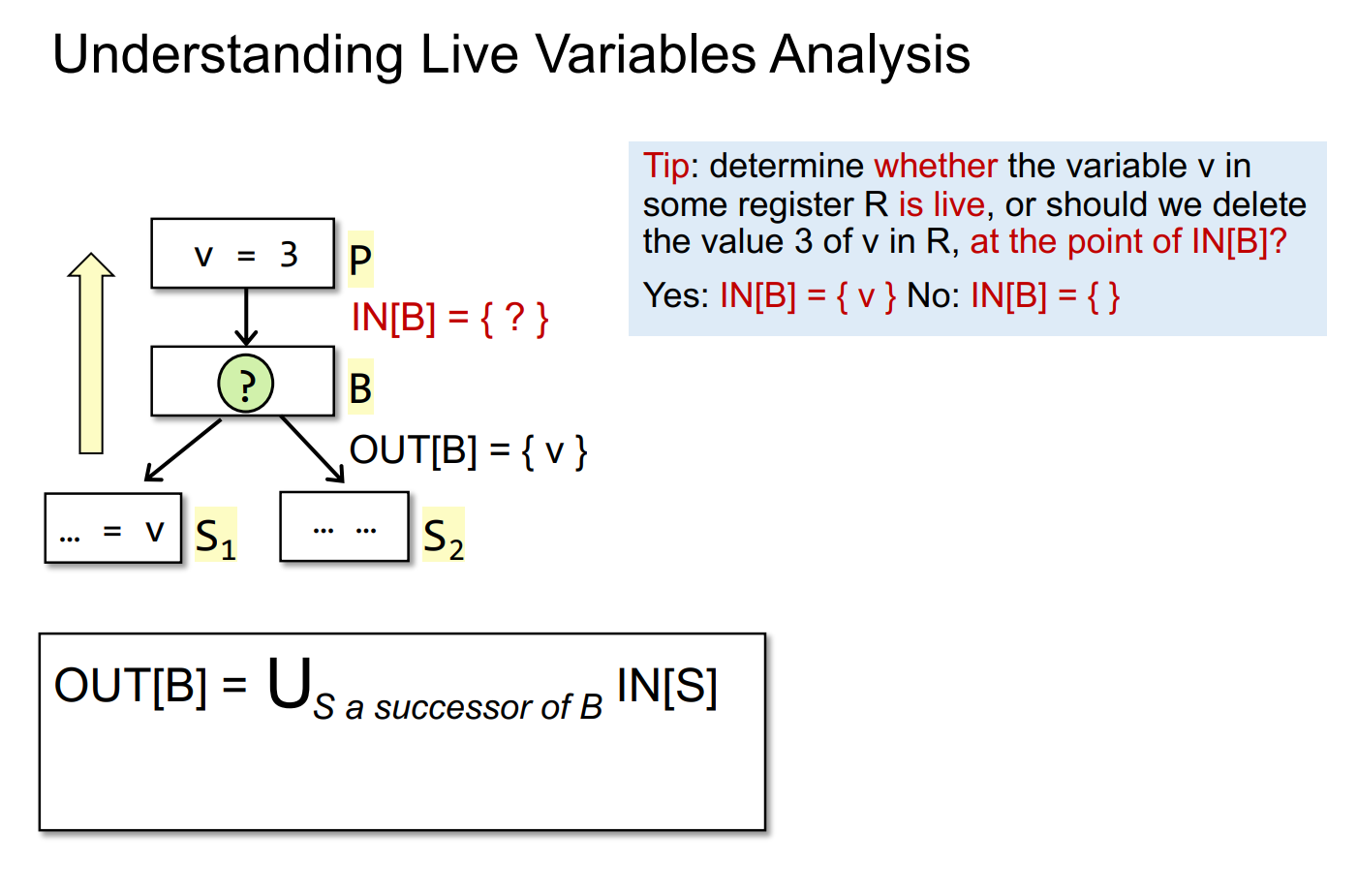
transfer functions

设计transfer functions计算IN[B]

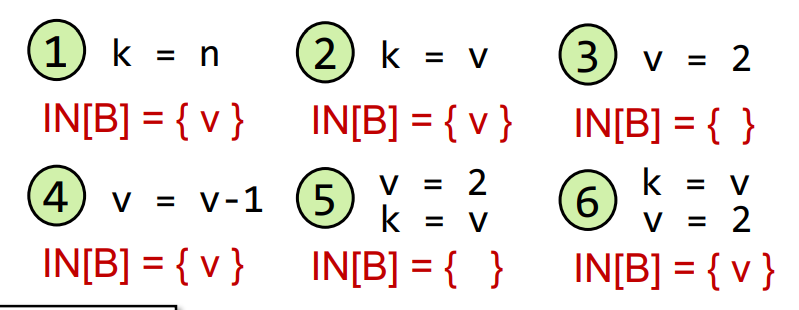
观察v是否在初始化后被重新定义(redefine)，4和6都在在redefine之前use了，所以也是live

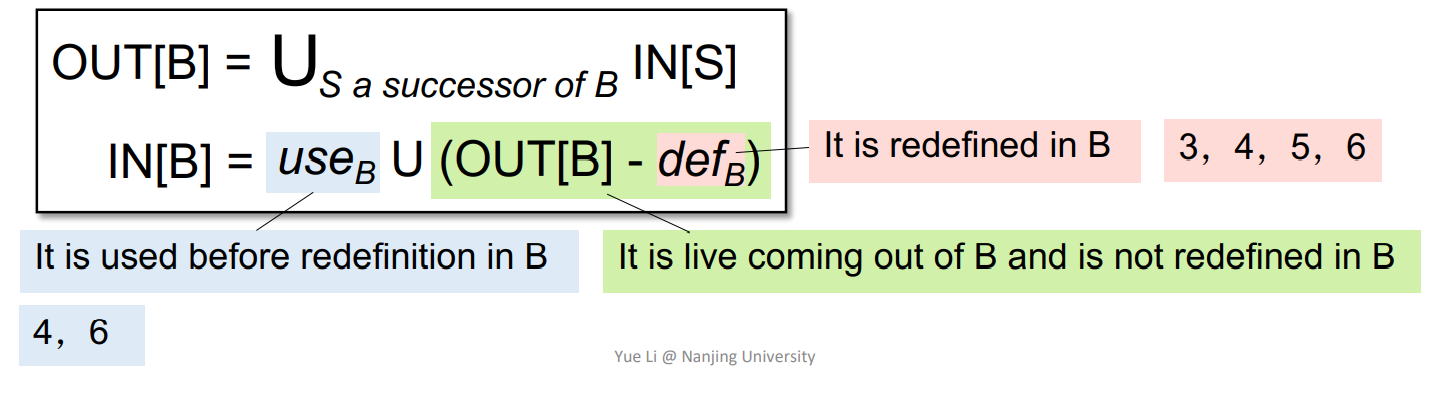
算法

从exit逆向分析，一般情况下，may analysis初始化为空，must analysis初始化为ALL

IN变了就继续迭代

例子

初始化

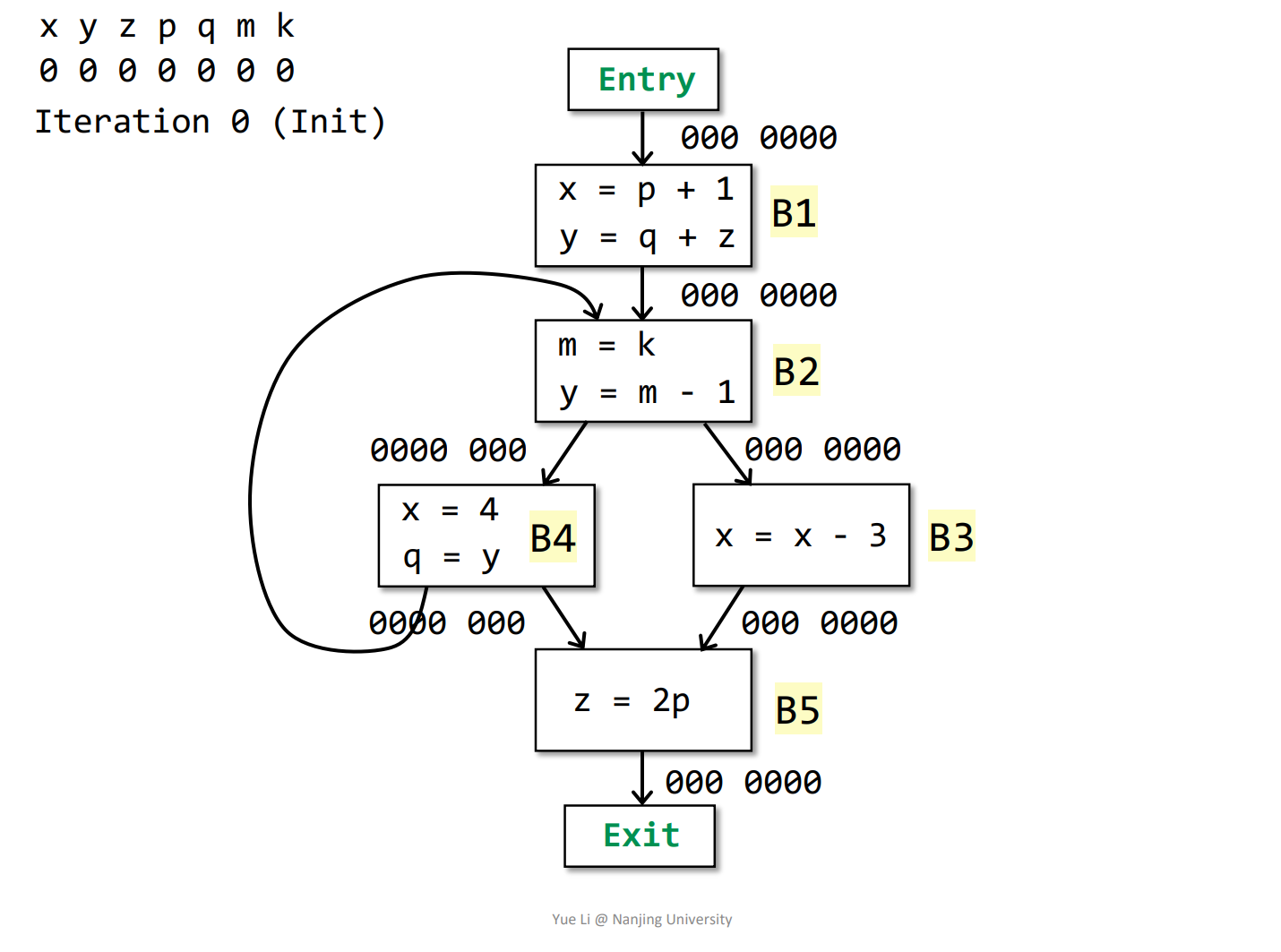
根据transfer funtion去逆向迭代算（建议跟着视频算一遍

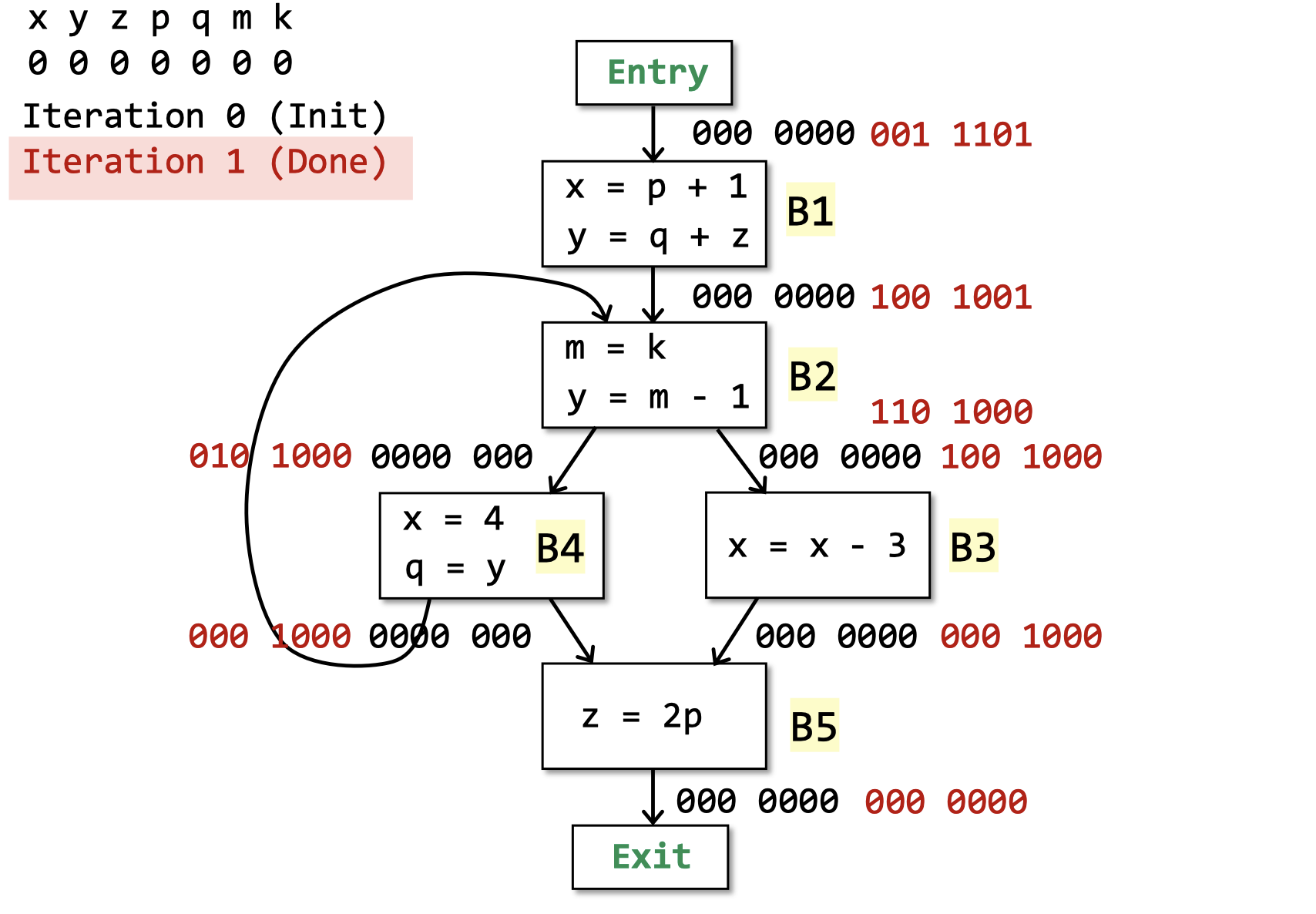
第一轮迭代，因为Basic Block的IN变了，继续迭代

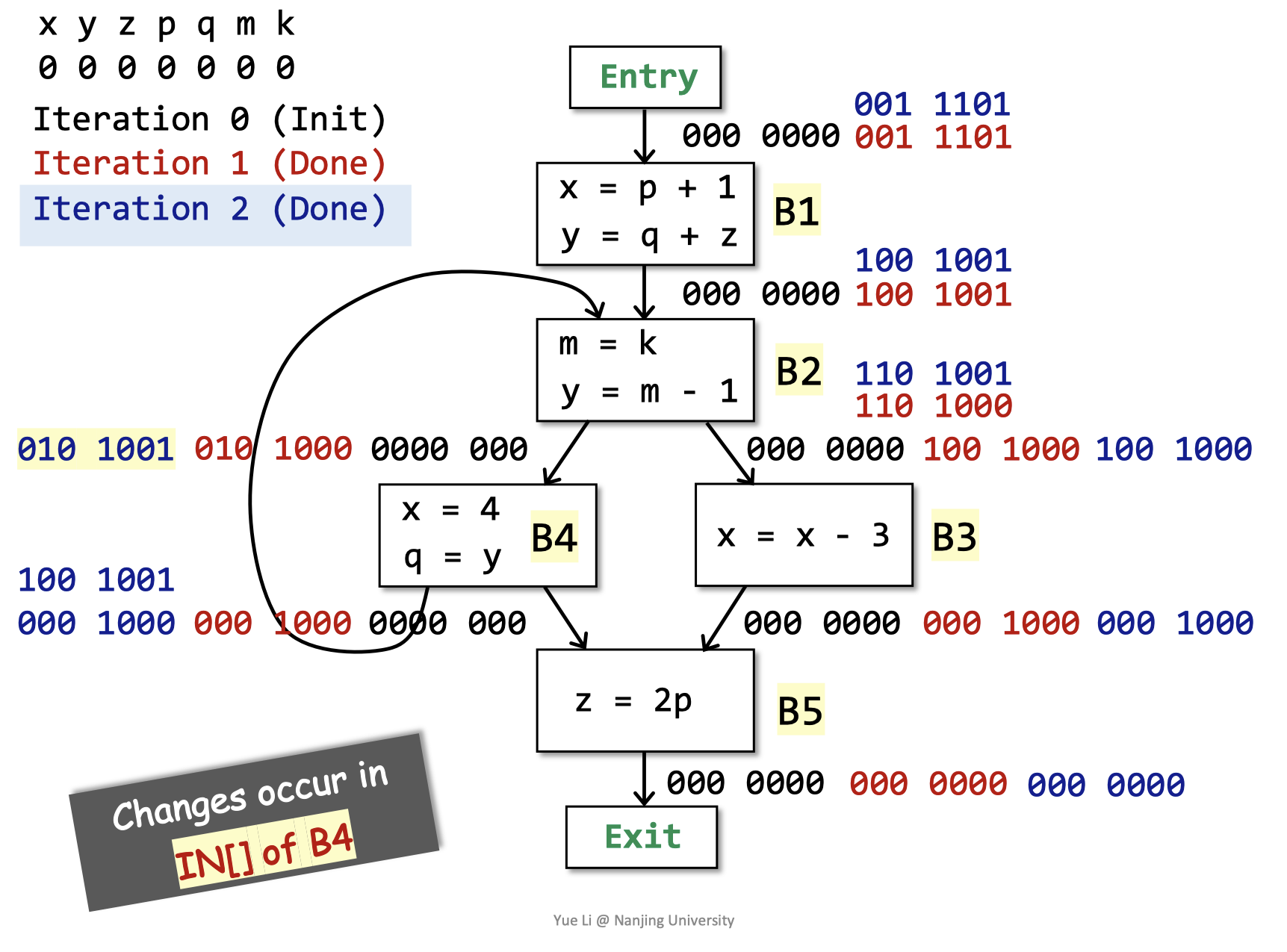
第二轮迭代

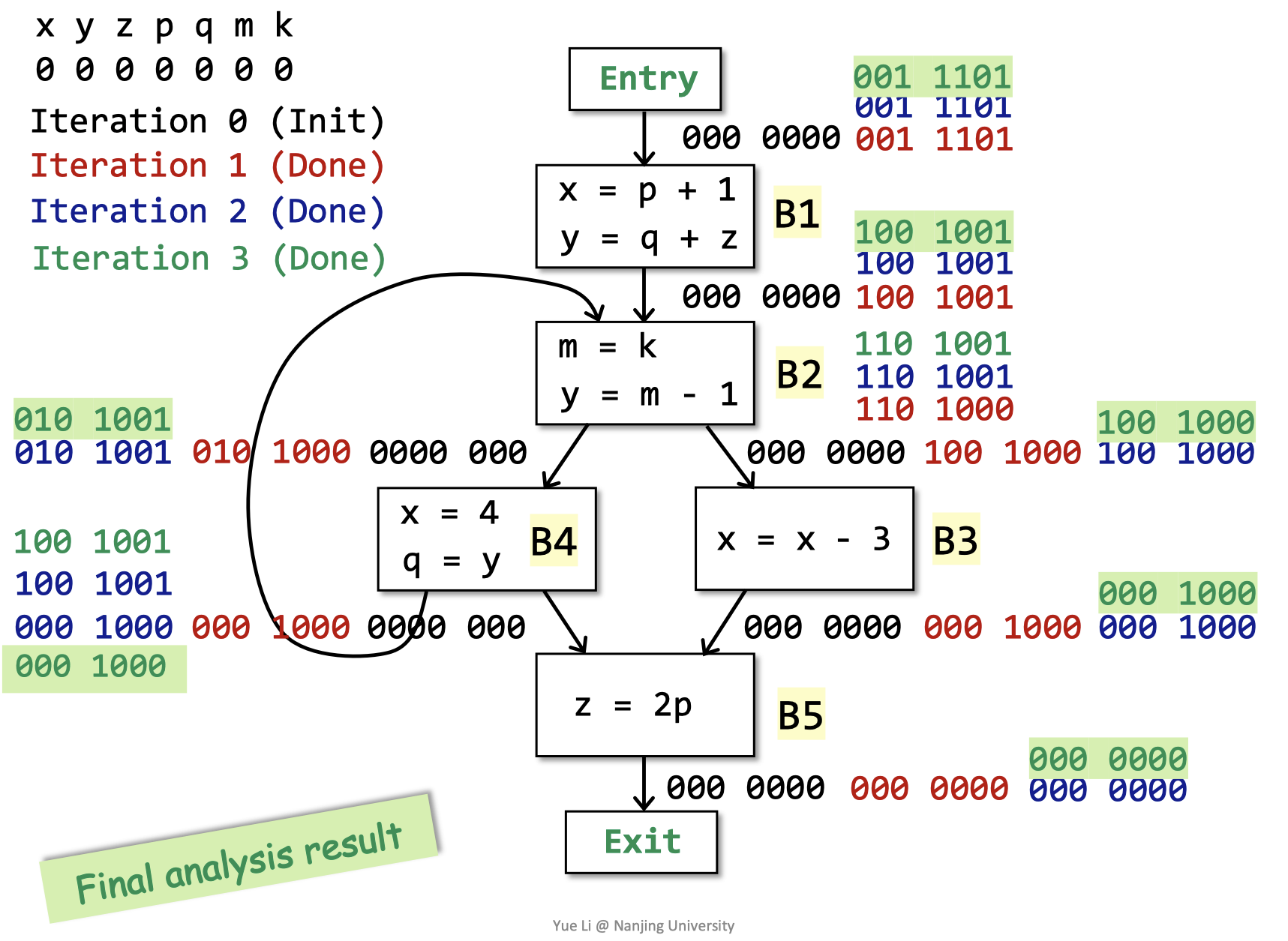
第三轮迭代结束

Available Expression Analysis

An expression x op y is available at program point p if (1) all paths from the entry to p must pass through the evaluation of x op y, and (2) after the last evaluation of x op y, there is no redefinition of x or y

程序点p处的表达式$x\ op\ y$可用需满足2个条件，一是从entry到p点必须经过$x\ op\ y$，二是最后一次使用$x\ op\ y$之后，没有重定义操作数x、y。（如果重定义了x 或 y，如$x = a\ op2\ b$，则原来的表达式$x\ op\ y$中的x或y就会被替代）。

这个算法应该是做编译优化，去除那些重复运算。

用n bit向量来抽象表示，0表示unavailable，1表示available

transfer functions

这是一个forward analysis

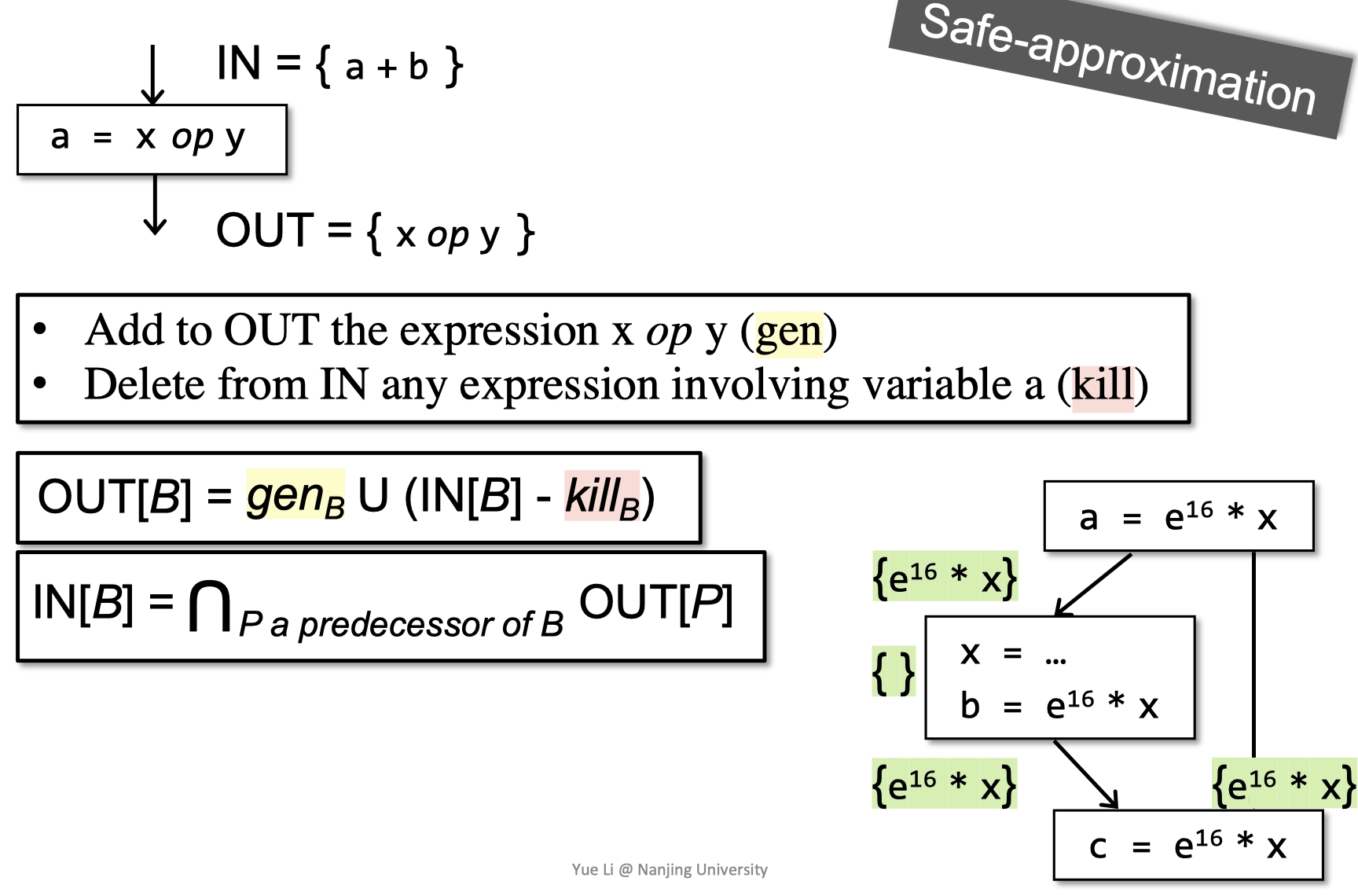
a被redefine了，a+b被kill掉。剩下x op y

右下的expression是available的

For safety of the analysis, it may report an expression as unavailable even if it is OUT truly = { x available op y } (must analysis -> under-approximation)

可以有漏报不能有误报。例如：上面的程序变为如下，x在编译前确定值为3，但未做常量传播，会导致漏报少一个优化，不会影响程序编译的正确性

算法

初始化入口为空，其他块为1

例子

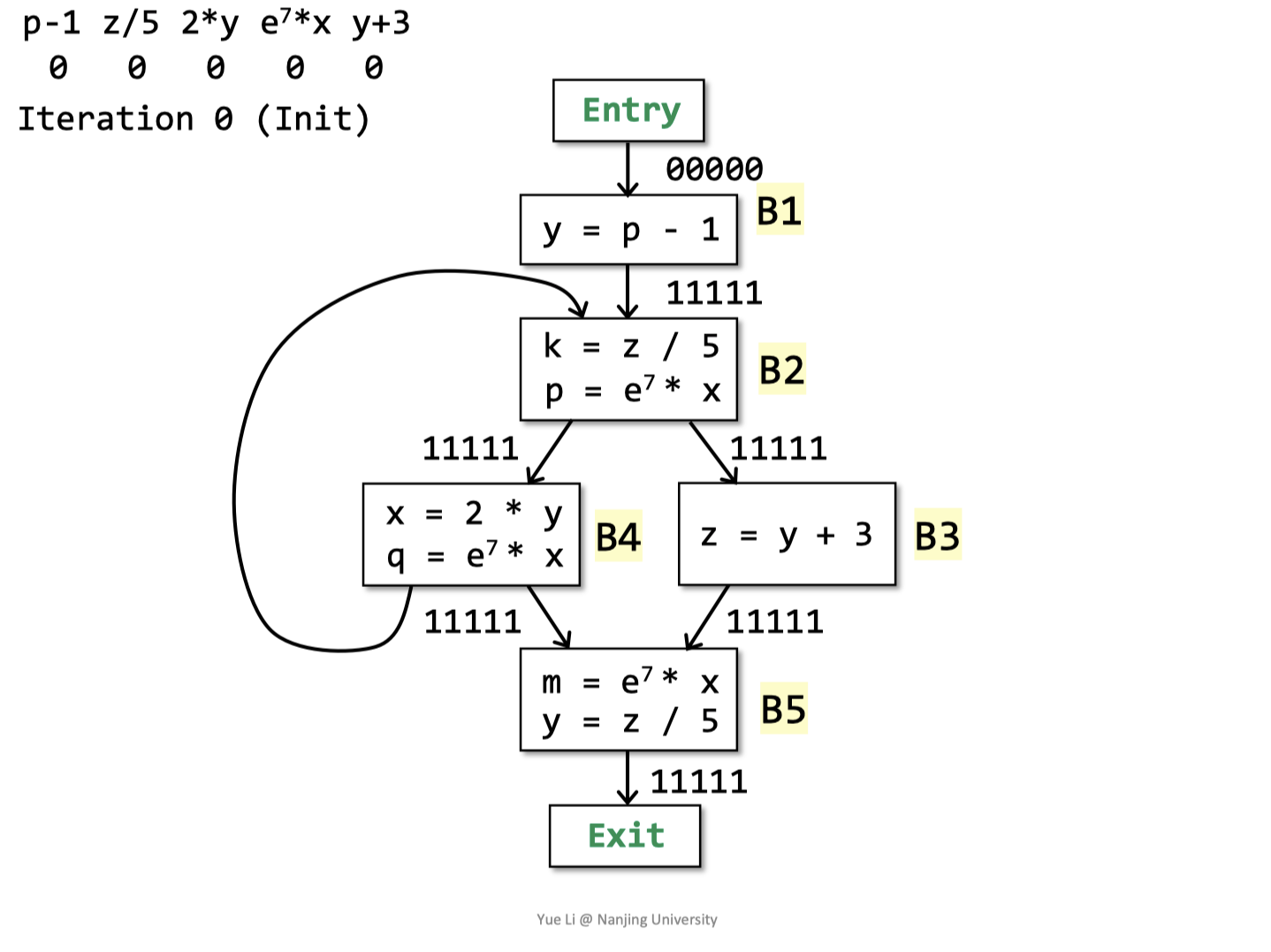
初始化

第一次迭代

迭代完成

三种技术对比

|&nbsp|Reaching Definitions|Live Variables|Available Expressions|

|::::

|Domain|Set of definitions|Set of variables|Set of expressions|

|Direction|forward|backward|forward|

|May/Must|May|May|Must|

|Boundary|OUT[entry]=$\emptyset$|IN[exit]=$\emptyset$|OUT[entry]=$\emptyset$|

|Initialization|OUT[B]=$\emptyset$|IN[B]=$\emptyset$|OUT[B]=$\cup$|

|Transfer function|OUT=gen $\cup$ (IN - kill)|OUT=gen $\cup$ (IN - kill)|OUT=gen $\cup$ (IN - kill)｜

|Meet|$\cup$|$\cup$|$\cup$|

总结

怎样判断是May还是Must？

Reaching Definitions只要从赋值语句到点p存在1条路径，则为reaching，结果不一定正确；（May）

Live Variables表示只要从点p到Exit存在1条路径使用了变量v，则为live，结果不一定正确；（May）

Available Expressions表示从Entry到点p的每一条路径都经过了该表达式，则为available，结果肯定正确。（Must）