Manacher算法求解回文字符串

Manacher算法可以在\(O(N)\)时间内求解出一个字符串的所有回文子串（正反遍历相同的字串）。

注：回文串显然有两种，一种是奇数长度，如abczcba，有一个中心字符z；另外一种是偶数个长度，如abccba，没有中心字符，下面提到暂时都是只查找奇数长度的字符串

要理解Manacher算法，首先假象一个随机生成的字符串，枚举每个字符作为中心，向两边不断拓展，判断是否相等，直到两边不相等或者走到边界为止，就可以得到每个字符为中心的最大回文长度了（记作\(f_i\)），显然第\(i\)个字符加上左右\(f_i\)的字符就可以构成\(i\)为中心的最长回文串\(S_{[i-f_i+1, i+f_i-1]}\)，而\(i\)为中心的更短的字串，显然也是回文串了，这样就求出了所有回文串。

void BF(char *s, int len, int *f) {
    for (int i = 1; i <= len; i++) {
        f[i] = 1;
        while (s[i+f[i]] == s[i-f[i]]) ++f[i];
    }
}

但是如果字符大量重叠（如abababab...），几乎每次拓展都会拓展到最边界，效率就会达到平方级。解决这个问题，就应该想到利用回文串的性质，利用已经得到的\(f_i\)来推出当前的\(f_i\)。

那么回文串有什么性质？首先是对称下标构成的字串肯定对称（比如abczcba，\(S_{[1, 3]}=S_{[7, 4]}\)），而且回文串的对称串依然是自己（定义）。所以，一个回文串中如果有另一个回文串，那么子串的对称下标肯定也构成了一个相同的回文串，可以直接推出来。换言之，如果我们知道一个回文串内左半边的对称串，就可以直接得到他右半边的对称串

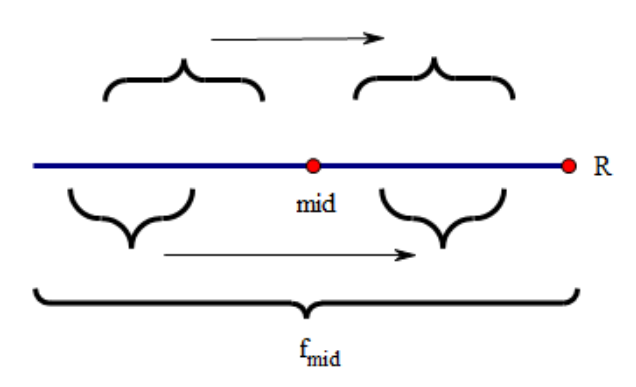
所以我们记录下达到过的最靠右的点和他的中心点（记为\(maxR\)和\(mid\)，当然你也可以只记录\(mid\)，用\(mid+f[mid]\)表示右边界）。只要枚举的\(i\)还在右边界以内，就尝试用\(f[mid*2-i]\)来更新\(f[i]\)。当然如果左半边回文串的最长左边界\(i-f[i]+1\)已经不在\(mid\)的回文范围内了，那就顶到最左边，把\(f[i]\)更新为\(f[mid]+mid-i\)（也就是最右边\(maxR\)处）。这时就需要继续往后更新，将\(maxR\)往右拓展。

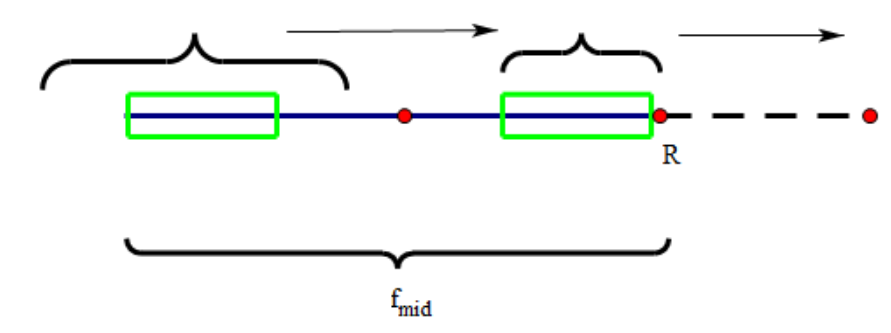
这里是一份参考代码，这里\(maxR\)是开区间。和上面的暴力一样没有做边界特判，应该将\(S[0]和S[len+1]\)设为两个原字符串中没有且不相等的字符（否则可能加上两端，多一个回文串，然后再往外走导致越界）。显然\(f[i]\)取\(f[mid]+mid-i\)时才会执行之后的更新。

void Manacher(char *s, int len, int *f) {
    static int maxR, mid;
    for (int i = 1; i <= len; i++) {
        f[i] = (i < maxR) ? min(f[mid*2-i], f[mid]+mid-i) : 1;
        while (s[i+f[i]] == s[i-f[i]]) ++f[i];
        if (i + f[i] > maxR)
            maxR = (mid = i) + f[i];
    }
}

那么为什么只需要这一个优化就可以做到线性呢？因为这样已经可以做到每个字符只被访问一次（算上和后面的字符比较相等就是两次）。回看第一张图，\(maxR\)左侧是已经访问过的，右侧是没有访问过的。这些已经访问过但\(i\)还没有遍历到的位置都可以\(O(1)\)求解，而\(maxR\)只会不断向右移动，因此一定是\(O(N)\)的。其本质就是利用回文串的性质避免了\(mid\)到\(maxR\)处的所有计算，只在往后更新的时候计算。

最后谈谈偶数长度回文串，偶数长度串的“中心”相当于于是字符之间的空隙。处理它们的一种方法是在每两个字符串之间加入不存在于原字符串的字符（如#），然后在执行算法，此时以#为中心的回文串就是偶数回文串。或者先做奇数长度，然后找到所有满足\(S[i]==S[i+1]\)的下标，将他们看作“一个中心“后进行拓展。

for (int i = 1; i <= len; i++)
    s0[(i << 1) - 1] = s[i], s0[i << 1] = '#';