递归与分治策略之棋盘覆盖Java实现
递归与分治策略之棋盘覆盖
一、问题描述
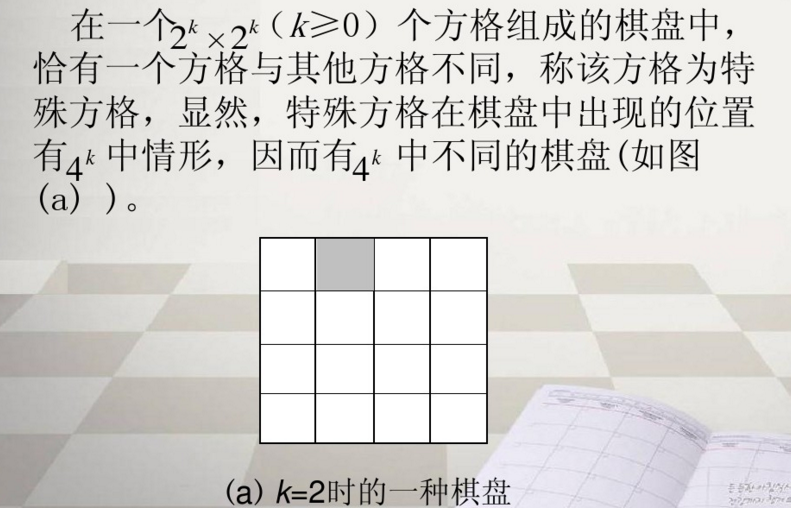
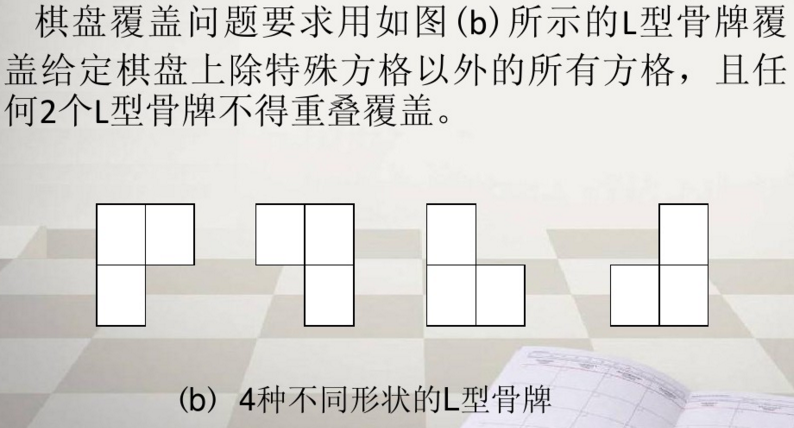
二、过程详解
1、棋盘如下图,其中有一特殊方格:16*16
 、
、
2、第一个分割结果:8*8
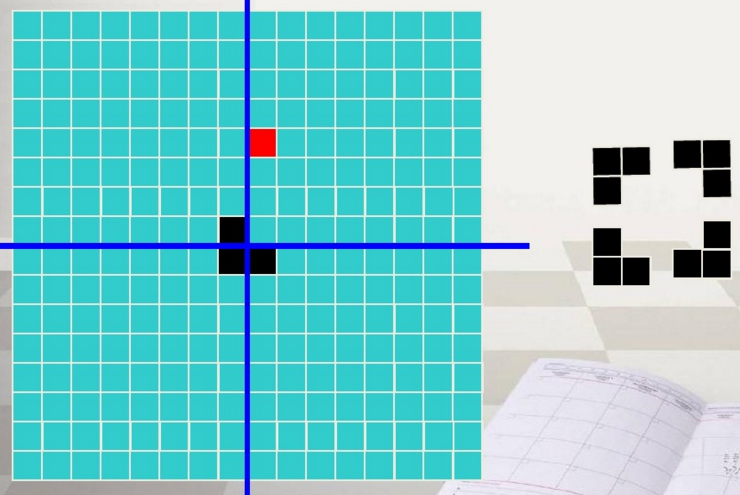
3、第二次分割结果:4*4
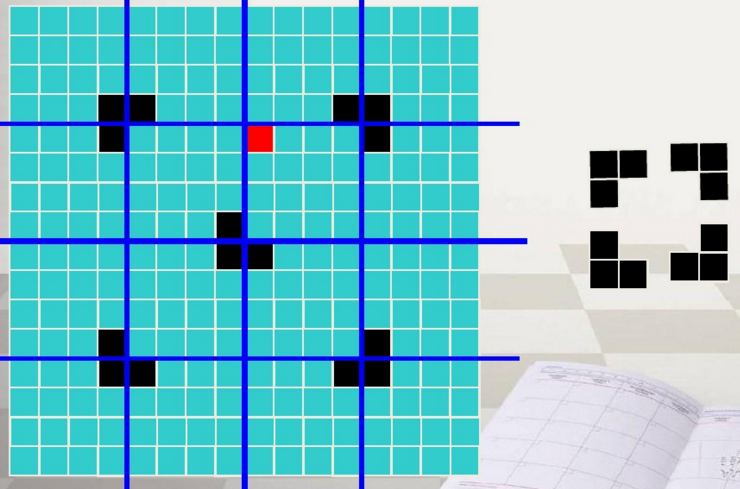
4、第三次分割结果:2*2

5、第四次分割结果:1*1

6、第一次分割后子棋盘的覆盖效果

三、代码实现
package cn.com.zfc.everyday.test; import java.util.Scanner; /**
*
* @title ChessboardCoverage
* @describe 棋盘覆盖:
* 利用分治法,将方形棋盘分成4部分,如果该特殊点在某一部分,我们就去递归他,如果不在某一部分,我们假设一个点为特殊点,同样递归下去,知道全覆盖。
*
* 左上角的子棋盘(若不存在特殊方格):则将该子棋盘右下角的那个方格假设为特殊方格;
* 右上角的子棋盘(若不存在特殊方格):则将该子棋盘左下角的那个方格假设为特殊方格;
* 左下角的子棋盘(若不存在特殊方格):则将该子棋盘右上角的那个方格假设为特殊方格;
* 右下角的子棋盘(若不存在特殊方格):则将该子棋盘左上角的那个方格假设为特殊方格;
* @author 张富昌
* @date 2017年4月9日下午7:36:15
*/
public class ChessboardCoverage {
// 定义棋盘的大小:2^k,需要的骨牌数是:(4^k-1)/3
private static int BOARD_SIZE = 8;
// 定义一个二维数组用来模拟棋盘
private static int[][] board = new int[BOARD_SIZE][BOARD_SIZE];
// 定义一个全局变量,用来记录骨牌的编号
private static int tile = 0; public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("棋盘的大小为:" + BOARD_SIZE);
System.out.println("请输入特殊方格所在的行号:");
int dr = scanner.nextInt();
System.out.println("请输入特殊方格所在的列号:");
int dc = scanner.nextInt();
scanner.close();
// 行号和列号与二位数组的下标相差 1
chessBoard(0, 0, dr - 1, dc - 1, BOARD_SIZE);
System.out.println("特殊方块在第 " + dr + " 行第 " + dc + "列,覆盖后的棋盘:");
// 输出棋盘
printBoard();
} /**
*
* @param tr:棋盘左上角方格的行号
* @param tc:棋盘左上角方格的列号
* @param dr:特殊方格所在的行号
* @param dc:特殊方格所在的列号
* @param size:当前棋盘的大小
*/
private static void chessBoard(int tr, int tc, int dr, int dc, int size) {
/* 1、当前棋盘的大小是 1 就返回 */
if (size == 1) {
return;
}
int t = tile++;
// 分割棋盘,棋盘大小减半
int s = size / 2; /* 2、覆盖左上角子棋盘 */
if (dr < tr + s && dc < tc + s) {
// 特殊方格在此棋盘中
chessBoard(tr, tc, dr, dc, s);
} else {
// 特殊方格不在此棋盘中,用 t 号骨牌覆盖右下角
board[tr + s - 1][tc + s - 1] = t;
// 覆盖其余方格
chessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
} /* 3、覆盖右上角子棋盘 */
if (dr < tr + s && dc >= tc + s) {
// 特殊方格在此棋盘中
chessBoard(tr, tc + s, dr, dc, s);
} else {
// 特殊方格不在此棋盘中,用 t 号骨牌覆盖左下角
board[tr + s - 1][tc + s] = t;
// 覆盖其余方格
chessBoard(tr, tc + s, tr + s - 1, tc + s, s);
} /* 4、覆盖左下角子棋盘 */
if (dr >= tr + s && dc < tc + s) {
// 特殊方格在此棋盘中
chessBoard(tr + s, tc, dr, dc, s);
} else {
// 特殊方格不在此棋盘中,用 t 号骨牌覆盖右上角
board[tr + s][tc + s - 1] = t;
// 覆盖其余方格
chessBoard(tr + s, tc, tr + s, tc + s - 1, s);
} /* 5、覆盖左下角子棋盘 */
if (dr >= tr + s && dc >= tc + s) {
// 特殊方格在此棋盘中
chessBoard(tr + s, tc + s, dr, dc, s);
} else {
// 特殊方格不在此棋盘中,用 t 号骨牌覆盖右上角
board[tr + s][tc + s] = t;
// 覆盖其余方格
chessBoard(tr + s, tc + s, tr + s, tc + s, s);
}
} // 输出棋盘
private static void printBoard() {
for (int i = 0; i < BOARD_SIZE; i++) {
for (int j = 0; j < BOARD_SIZE; j++) {
System.out.print(board[i][j] + "\t");
}
System.out.println("\n");
}
} }
测试效果:
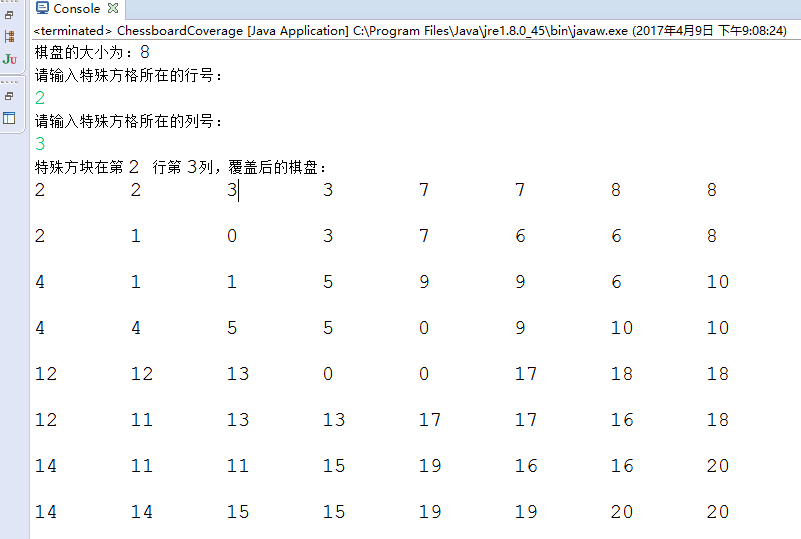
递归与分治策略之棋盘覆盖Java实现的更多相关文章
- 递归与分治策略之循环赛日程表Java实现
递归与分治策略之循环赛日程表 一.问题描述 设有n=2^k个运动员要进行网球循环赛.现要设计一个满足以下要求的比赛日程表: (1)每个选手必须与其他n-1个选手各赛一次: (2)每个选手一天只能参赛一 ...
- [图解算法] 归并排序MergeSort——<递归与分治策略>
#include"iostream.h" void Merge(int c[],int d[],int l,int m,int r){ ,k=l; while((i<=m)& ...
- [图解算法] 二分查找Binary-Search——<递归与分治策略>
#include"iostream.h" int BinarySearch(int a[],int left,int right,const int& x) { if(le ...
- [图解算法]线性时间选择Linear Select——<递归与分治策略>
#include <ctime> #include <iostream> using namespace std; template <class Type> vo ...
- 棋盘覆盖问题 (粉书 P230 【递归】** )
转载自:http://blog.csdn.net/akof1314/article/details/5423608 (赞) 在一个 2^k * 2^k 个方格组成的棋盘中,若恰有一个方格与其它方格不 ...
- 棋盘覆盖(大数阶乘,大数相除 + java)
棋盘覆盖 时间限制:3000 ms | 内存限制:65535 KB 难度:3 描述 在一个2k×2k(1<=k<=100)的棋盘中恰有一方格被覆盖,如图1(k=2时),现用一缺角的 ...
- 棋盘覆盖问题(算法分析)(Java版)
1.问题描述: 在一个2k×2k个方格组成的棋盘中,若有一个方格与其他方格不同,则称该方格为一特殊方格,且称该棋盘为一个特殊棋盘.显然特殊方格在棋盘上出现的位置有种情形.因而对任何 k≥0,有4k种不 ...
- js算法:分治法-棋盘覆盖
在一个 2^k * 2^k 个方格组成的棋盘中,若恰有一个方格与其他方格不同.则称该方格为一特殊方格,称该棋盘为一特殊棋盘.显然特殊方格在棋盘上出现的位置有 4^k 种情形.因而对不论什么 k> ...
- NYOJ 45 棋盘覆盖 模拟+高精度
题意就不说了,中文题... 小白上讲了棋盘覆盖,于是我就挖了这题来做. 棋盘覆盖的推导不是很难理解,就是分治的思想,具体可以去谷歌下. 公式就是f(k) = f(k - 1) * 4 + 1,再化解下 ...
随机推荐
- [转]Ubuntu下ROS开发环境搭建(QT+ros_qtc_plugin)
ROS与C++入门教程-搭建开发环境(QT+ros_qtc_plugin) PS : 在“安装ros_qtc_plugin插件”这一步中,原文提到“ Ubuntu 14.04使用apt-get方式安装 ...
- 2016.5.18——leetcode:Majority Element
Majority Element 本题收获: 1.初步了解hash,nth_element的用法 2.题目的常规思路 题目: Given an array of size n, find the ma ...
- SolrJ案例实现搭建环境——(十五)
案例
- 【CTF WEB】文件包含
文件包含 题目要求: 请找到题目中FLAG 漏洞源码 <meta charset='utf-8'> <center><h1>文件阅读器</h1>< ...
- verilog中wire与reg类型的区别
每次写verilog代码时都会考虑把一个变量是设置为wire类型还是reg类型,因此把网上找到的一些关于这方面的资料整理了一下,方便以后查找. wire表示直通,即只要输入有变化,输出马上无条件地反映 ...
- LINUX的DNS设置【转】
网卡DNS设置 用windos系统大家都知道,本地连接里面有一个DNS设置. 那么这个选项对应Linux系统的话就是在网卡配置文件,通过编辑vi /etc/sysconfig/network-scr ...
- 美国部分科技公司创始及IPO信息
作者:Ben.Z 时间:2018-04-19 做这份统计表格的目的是为了更好地了解当下美国的IT发展,搞清楚那些耳熟能详的名词的来源. 原文是用WPS统计的,本文仅展示截图. 创始人年龄分析: 1.上 ...
- 虚拟机 windows xp sp3 原版
原版的镜像:http://www.7xdown.com/Download.asp?ID=3319&URL=http://d5.7xdown.com/soft2/&file=Window ...
- 洛谷P3396哈希冲突
传送门啦 非常神奇的分块大法. 这个题一看数据范围,觉得不小,但是如果我们以 $ \sqrt(x) $ 为界限,数据范围就降到了 $ x < 400 $ 我们设数组 $ f[i][j] $ 表示 ...
- (一)问候 Log4j 你好
第一节: Log4j 简介 Log4j -------- log for java(java的日志) 是java主流的日志框架,提供各种类型,各种存储,各种格式,多样化的日志服务: 在爬虫领域,主要用 ...
