PGM学习之五 贝叶斯网络

本文的主题是“贝叶斯网络”（Bayesian Network）

贝叶斯网络是一个典型的图模型，它对感兴趣变量（variables of interest）及变量之间的关系（relationships）进行建模。当将贝叶斯模型与统计技术一起使用时，这种图模型分析数据具有如下几个优势：

(1)    贝叶斯学习能够方便的处理不完全数据。例如考虑具有相关关系的多个输入变量的分类或回归问题，对标准的监督学习算法而言，变量间的相关性并不是它们处理的关键因素，当这些变量中有某个缺值时，它们的预测结果就会出现很大的偏差。而贝叶斯学习则提供了较为直观的概率关联关系模型。
(2)    贝叶斯学习能够学习变量间的因果关系。因果关系是数据挖掘中极为重要的模式。原因有二：在数据分析中，因果关系有利于对领域知识的理解；在干扰较多时，便于作出精确的预测。
(3)    贝叶斯网络与贝叶斯统计相结合能够充分利用领域知识和样本数据的信息。任何从事过实际建模任务的人都会知道先验信息或领域知识在建模方面的重要性，尤其是在样本数据稀疏或数据较难获得的时候，一些商业方面的专家系统完全根据领域专家知识来构建就是一个很好的例证。贝叶斯网络用弧表示变量间的依赖关系，用概率分布表来表示依赖关系的强弱，将先验信息与样本知识有机结合起来。

贝叶斯学习理论在数据挖掘中获得了成功的应用。对贝叶斯学习理论研究最大的动力就是它在实际应用中的巨大作用和潜力。目前，贝叶斯学习理论已成功地应用到智能用户接口、信息滤波、车辆自动导航、武器制导、医疗诊断、经济预测和文本分类等诸多领域。

(4)贝叶斯统计方法可以和贝叶斯网络一起使用，避免了数据过度拟合（the overfiting of data）。

本文，主要讨论如何从先验知识构造贝叶斯网络，总结如何使用贝叶斯统计方法来改进贝叶斯网络的构造方法 。同时，得益于前人的工作，本文还将讨论贝叶斯网络的参数学习方法。贝叶斯网络所依赖的一个核心概念是条件独立，Conditional Independence。

一 基本概念

贝叶斯网络(Bayesian network)，又称有向无环图模型(directed acyclic graphical model)，是一种概率图型模型，借由有向无环图(directed acyclic graphs, or DAGs )中得知一组随机变量{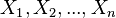}及其n组条件概率分配(conditional probability distributions, or CPDs)的性质。举例而言，贝叶斯网络可用来表示疾病和其相关症状间的概率关系；倘若已知某种症状下，贝叶斯网络就可用来计算各种可能罹患疾病之发生概率。
    一般而言，贝叶斯网络的有向无环图中的节点表示随机变量，它们可以是可观察到的变量，抑或是隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有因果关系或是非条件独立的；而节点中变量间若没有箭头相互连接一起的情况就称其随机变量彼此间为条件独立。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(descendants or children)”，两节点就会产生一个条件概率值。
    令G = (I,E)表示一个有向无环图(DAG)，其中I代表图形中所有的节点的集合，而E代表有向连接线段的集合，且令X = (Xi)i ∈ I为其有向无环图中的某一节点i所代表之随机变量，若节点X的联合概率分配可以表示成:

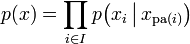
则称X为相对于一有向无环图G 的贝叶斯网络，其中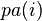表示节点i之“因”。
    对任意的随机变量，其联合分配可由各自的局部条件概率分配相乘而得出：
       
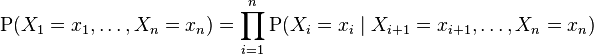
   依照上式，我们可以将一贝叶斯网络的联合概率分配写成：
       , 对每个相对于Xi的“因”变量Xj 而言)

 

    上面两个表示式之差别在于条件概率的部分，在贝叶斯网络中，若已知其“因”变量下，某些节点会与其“因”变量条件独立，只有与“因”变量有关的节点才会有条件概率的存在。这就是后面我们要重点理解的，影响因子的推理规则。

二 独立与分割

独立：令X,Y,Z代表概率事件。如果X,Y的概率满足P(X,Y)=P(X)*P(Y)，那么就称X和Y相互独立（independent）；

如果P(X,Y,Z)正比于φ1(X,Z)*φ2(Y,Z)，那么就称X和Y在条件X下独立。

有向分割(D-Separated)：对于变量集合Z中任意一个变量，如果X和Y之间没有活动路径，那么就称X和Y为有向分割。X，Y和Z中所有变量均为图G的点。

三 推理（Inference）

贝叶斯络可以利用变量间的条件独立对联合分布进行分解，降低参数个数。推理(inference)是通过计算来回答查询的过程。

1 变量消元算法(Variable elimination)

利用概率分解降低推理复杂度。

@ 使得运算局部化。消元过程实质上就是一个边缘化的过程。

@ 最优消元顺序：最大势搜索，最小缺边搜索

2. 团树传播算法
利用步骤共享来加快推理的算法。

团树（clique tree）是一种无向树，其中每一个节点代表一个变量集合，称为团(clique)。团树必须满足变量连通性，即包含同一变量的所有团所导出的子图必须是连通的。
用团树组织变量消元的算法。计算共享
团树传播算法基本步骤：

将贝叶斯网络转化为团树

团树初始化

在团树中选一个团作为枢纽

全局概率传播：CollectMessage; DistributeMessage

边缘化，归一化

四 构建贝叶斯网络

构建贝叶斯网络包括以下二部分内容:     (1)变量的定义;     (2)结构学习;     (3)参数学习。        

这二个任务之间一般是顺序进行的，然}fu在构造过程中一般需要在以下 两个方面作折中:一方面为了达到足够的精度，需要构建一个足够大的、丰富的网络模型;另一方面，要考虑构建、维护模型的费用和考虑概率推理的 复杂性。

一般来讲，复杂的模型结构它的概率推理的复杂性也较高，这往往是影响贝叶斯网络效率的一个重要方面。实际上建立一个贝叶斯网络往往 是上述二个过程迭代地、反复地交互过程。      

第一个任务主要是在领域专家的指导下选取适肩{的研究问题领域的变 量，同时在有些情况下也需要一定的策略从专家提供的变量中选择重要的因 子。

第二个任务是构建贝叶斯网络的关键点也是难点所在，主要是构建 出一个有向无环图并给出图中每个结点的分布参数，即每个节点都对应一个 条件概率分布表(CPT)。      

一般情况下，有二种不同方式来构造贝叶斯网络。      

(1)完整学习。这种方式完全由人主观定义贝叶斯网络结构及参数，由 领域专家确定贝叶斯网中的变量，通过专家的知识来确定贝叶斯网络的结 构，并指定它的分布参数。这种方式构造的贝叶斯网完全在专家的指导下进 行，由十人类获得知识的有限性，导致构建的网络与实践中积累下的数据具 有很大的偏差。     

 (2)部分学习。这种方式由人主观定义贝叶斯网络中的结点变量，然后 通过大量的训练数据来学习贝叶斯网的结构和参数。这种方式完全是一种数据驱动的方法，具有很强的适应性。随着人工智能、数据挖掘和机器学 习的不断发展，使得这种方法成为可能。如何从数据中学习贝叶斯网的结构 和参数己经成为贝叶斯网络研究的热点之一。      

(3)第二种方式是以上两种方式的结合。由领域专家确定贝叶斯网络中 的结点变量，通过专家的知识来指定网络的结构，再通过机器学习的方法从 数据中学习网络的参数。