条件随机场CRF介绍

链接：https://mp.weixin.qq.com/s/BEjj5zJG3QmxvQiqs8P4-w

softmax

CRF主要用于序列标注问题，可以简单理解为是给序列中的每一帧，既然是分类，很自然想到将这个序列用CNN或者RNN进行编码后，接一个全连接层用softmax激活，如下图所示

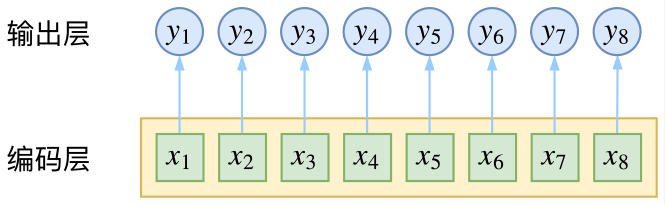
逐帧softmax并没有直接考虑输出的上下文关联

条件随机场

然而，当我们设计标签时，比如用s、b、m、e的4个标签来做字标注法的分词，目标输出序列本身会带有一些上下文关联，比如s后面就不能接m和e，等等。逐标签softmax并没有考虑这种输出层面的上下文关联，所以它意味着把这些关联放到了编码层面，希望模型能自己学到这些内容，但有时候会“强模型所难”。

而CRF则更直接一点，它将输出层面的关联分离了出来，这使得模型在学习上更为“从容”：

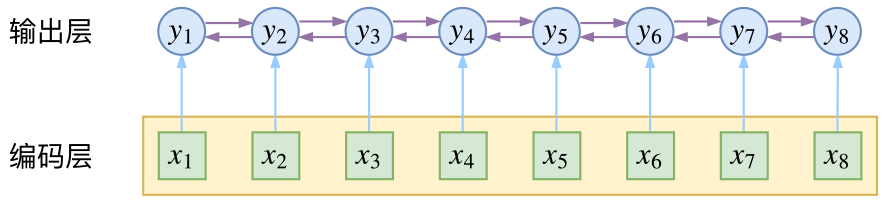
CRF在输出端显式地考虑了上下文关联

数学

当然，如果仅仅是引入输出的关联，还不仅仅是CRF的全部，CRF的真正精巧的地方，是它以路径为单位，考虑的是路径的概率。

模型概要

假如一个输入有nn帧，每一帧的标签有kk中可能性，那么理论上就有knkn中不同的输入。我们可以将它用如下的网络图进行简单的可视化。在下图中，每个点代表一个标签的可能性，点之间的连线表示标签之间的关联，而每一种标注结果，都对应着图上的一条完整的路径。

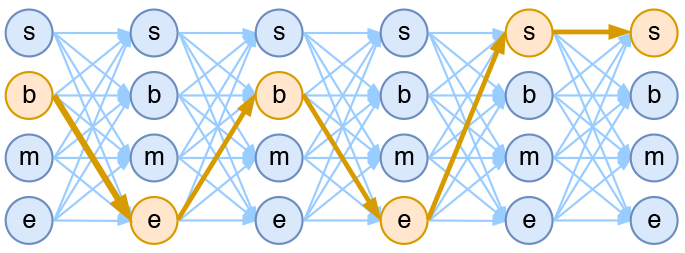
4tag分词模型中输出网络图

而在序列标注任务中，我们的正确答案是一般是唯一的。比如“今天天气不错”，如果对应的分词结果是“今天/天气/不/错”，那么目标输出序列就是bebess，除此之外别的路径都不符合要求。换言之，在序列标注任务中，我们的研究的基本单位应该是路径，我们要做的事情，是从kⁿ条路径选出正确的一条，那就意味着，如果将它视为一个分类问题，那么将是kⁿ类中选一类的分类问题！

这就是逐帧softmax和CRF的根本不同了：个kⁿ分类问题。

具体来讲，在CRF的序列标注问题中，我们要计算的是条件概率

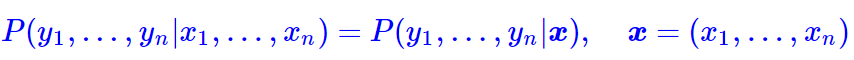
为了得到这个概率的估计，CRF做了两个假设：

假设一 该分布是指数族分布。

这个假设意味着存在函数f(y₁,…,y_n;x)，使得

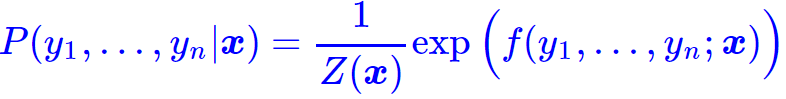
其中Z(x)是归一化因子，因为这个是条件分布，所以归一化因子跟x有关。这个f函数可以视为一个打分函数，打分函数取指数并归一化后就得到概率分布。

假设二 输出之间的关联仅发生在相邻位置，并且关联是指数加性的

这个假设意味着f(y₁,…,y_n;x)可以更进一步简化为

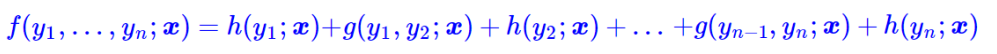
这也就是说，现在我们只需要对每一个标签和每一个相邻标签对分别打分，然后将所有打分结果求和得到总分。

线性链CRF

管已经做了大量简化，但一般来说，上式所表示的概率模型还是过于复杂，难以求解。于是考虑到当前深度学习模型中，RNN或者层叠CNN等模型已经能够比较充分捕捉各个y与输出x的联系，因此，我们不妨考虑函数g跟x无关，那么

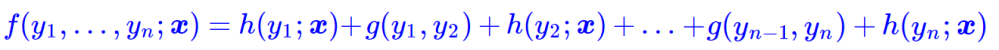
这时候g实际上就是一个有限的、待训练的参数矩阵而已，而单标签的打分函数h(y_i;x)我们可以通过RNN或者CNN来建模。因此，该模型是可以建立的，其中概率分布变为

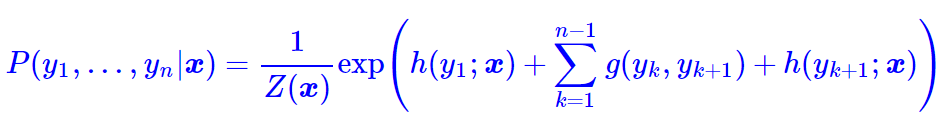
这就是线性链CRF的概念。

归一化因子

为了训练CRF模型，我们用最大似然方法，也就是用

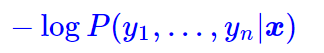
作为损失函数，可以算出它等于

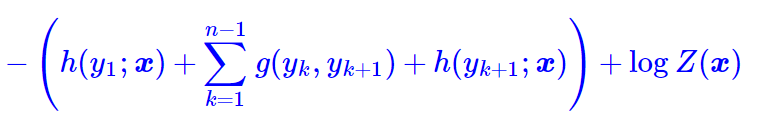
其中第一项是原来概率式的分子的对数，它目标的序列的打分，虽然它看上去挺迂回的，但是并不难计算。真正的难度在于分母的对数logZ(x)这一项。

归一化因子，在物理上也叫配分函数，在这里它需要我们对所有可能的路径的打分进行指数求和，而我们前面已经说到，这样的路径数是指数量级的（kⁿ），因此直接来算几乎是不可能的。

事实上，归一化因子难算，几乎是所有概率图模型的公共难题。幸运的是，在CRF模型中，由于我们只考虑了临近标签的联系（马尔可夫假设），因此我们可以递归地算出归一化因子，这使得原来是指数级的计算量降低为线性级别。具体来说，我们将计算到时刻t的归一化因子记为Z_t，并将它分为k个部分

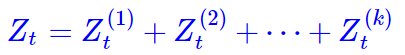
其中分别是截止到当前时刻t中、以标签1,…,k为终点的所有路径的得分指数和。那么，我们可以递归(DP)地计算

它可以简单写为矩阵形式

的各个标签的打分的指数，即H(y_t+1|x)=e^h(y_t+1|x)，也是一个向量。Z_tG这一步是矩阵乘法，得到一个向量，而⊗是两个向量的逐位对应相乘

归一化因子的递归计算图示。从t到t+1时刻的计算，包括转移概率和j+1节点本身的概率

动态规划

写出损失函数−logP(y₁,…,y_n|x)后，就可以完成模型的训练了。假设现在有一句用于测试的句子，根据训练好的模型，我们可以算出每个时刻t对应的h值，以及CRF对应的转移概率。下面就可以进行前向动态规划求最大概率，并保存转移状态。 令dp[t][y]: 表示t时刻标签为y的路径的最大概率，那么dp[t][y]=max dp[t-1][y'], y'=1,2,3,4。pre[t][y]: 表示从上一部转移过来的最优标签y'。