6，Stack

一，Stack简介

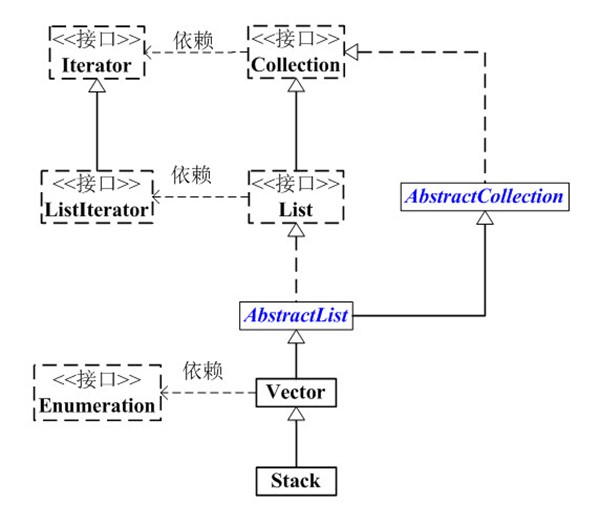
Stack是栈。它的特性是：先进后出(FILO, First In Last Out)。

java工具包中的Stack是继承于Vector(矢量队列)的，由于Vector是通过数组实现的，这就意味着，Stack也是通过数组实现的。

二，数据结构

Stack的数据结构如下：

底层的数据结构就是数组，数组元素类型为Object类型，即可以存放所有类型数据。对Stack类的实例的所有的操作底层都是基于数组的。

三，Stack源码

1，Stack结构

public class Stack<E> extends Vector<E> {
    // 构造函数
    public Stack() {
    }
    // push函数：将元素存入栈顶
    public E push(E item) {
        // 将元素存入栈顶。
        addElement(item);
        return item;
    }
    // pop函数：返回栈顶元素，并将其从栈中删除
    public synchronized E pop() {
        E       obj;
        int     len = size();
 
        obj = peek();
        removeElementAt(len - 1);
 
        return obj;
    }
    // peek函数：返回栈顶元素，不执行删除操作
    public synchronized E peek() {
        int     len = size();
 
        if (len == 0)
            throw new EmptyStackException();
        return elementAt(len - 1);
    }
    // 栈是否为空
    public boolean empty() {
        return size() == 0;
    }
    // 查找“元素o”在栈中的位置：由栈底向栈顶方向数
    public synchronized int search(Object o) {
        int i = lastIndexOf(o);
 
        if (i >= 0) {
            return size() - i;
        }
        return -1;
    }
    //版本ID。
    private static final long serialVersionUID = 1224463164541339165L;
}

2，总结

执行push时(即，将元素推入栈中)，是通过将元素追加的数组的末尾中。

执行peek时(即，取出栈顶元素，不执行删除)，是返回数组末尾的元素。

执行pop时(即，取出栈顶元素，并将该元素从栈中删除)，是取出数组末尾的元素，然后将该元素从数组中删除。

Stack继承于Vector，意味着Vector拥有的属性和功能，Stack都拥有。

四，Stack应用举例

public class TestStack {
    static long startTime = 0;
    static long endTime = 0;

    public static void main(String[] args) {
        Stack<String> stack = new Stack<String>();
        //添加数据到栈(先进后出)中
        stack.push("A");
        stack.push("B");
        stack.push("C");
        stack.push("D");
        stack.push("E");

        TestStack.test(stack);
        System.out.println("------------------------------------------");

        System.out.println("查找栈中数据的位置:" + stack.search("B"));
        System.out.println("------------------------------------------");

        // pup栈顶元素之后（会删除元素），遍历栈
        stack.pop();
        TestStack.test(stack);
        System.out.println("------------------------------------------");

        // peek栈顶元素之后（返回栈顶元素，不执行删除操作），遍历栈
        stack.peek();
        TestStack.test(stack);
    }

    public static void test(Stack<String> stack){
        System.out.print("栈中数据：");
        for (int i = 0; i < stack.size(); i++) {
            System.out.print(stack.get(i) + " ");
        }
        System.out.println();
    }
}

运行结果：