cuda编程-矩阵乘法（2）

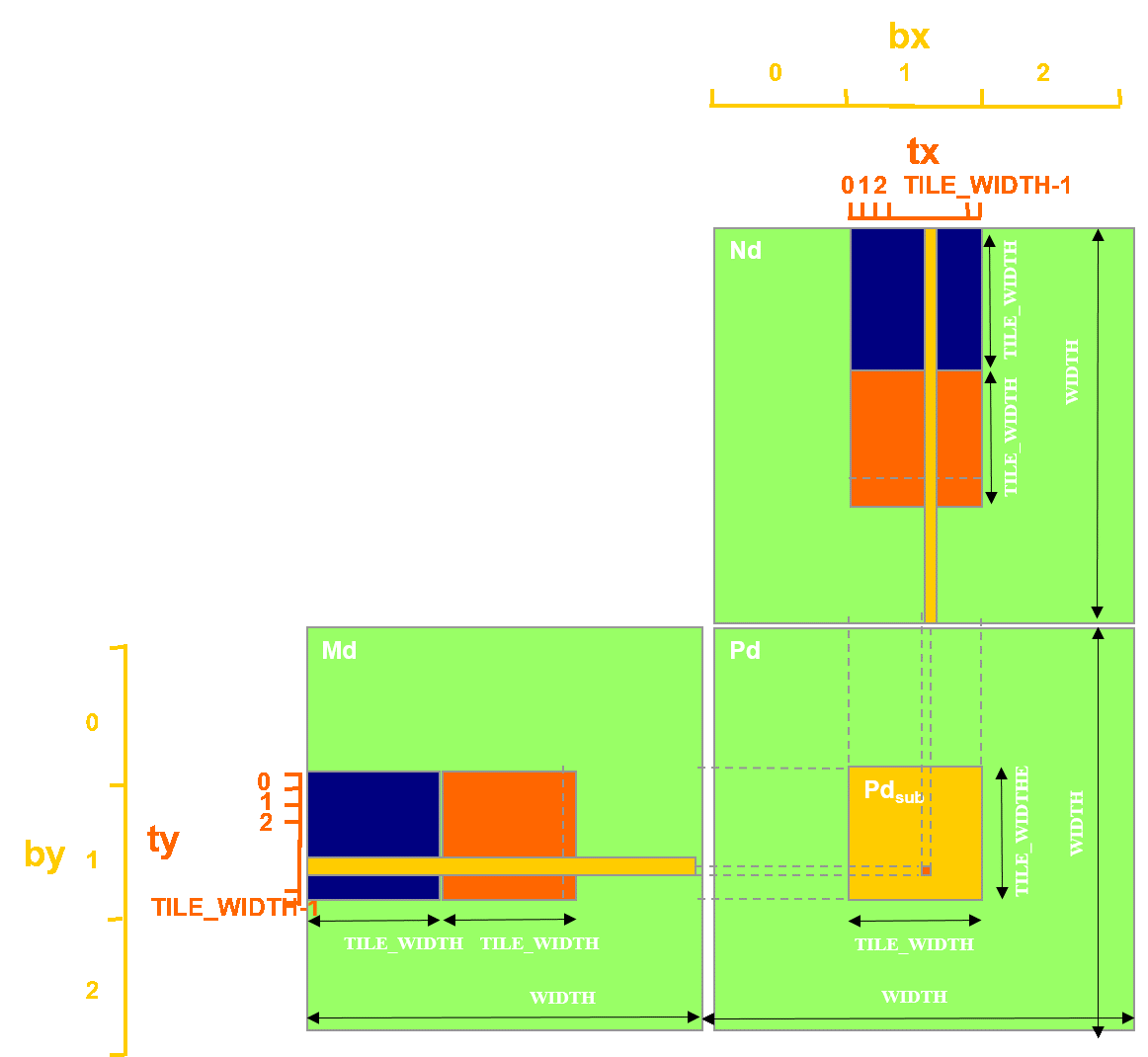
采用shared memory加速

代码

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <algorithm>
#include <cuda_runtime.h>
#include <device_launch_parameters.h>
#include "functions.h"

#define TILE_SIZE 16

__global__ void matrixMulKernel(float *C, float *A, float *B, int width, int height){
    __shared__ float tile_A[TILE_SIZE][TILE_SIZE];
    __shared__ float tile_B[TILE_SIZE][TILE_SIZE];
    unsigned int tx = threadIdx.x;
    unsigned int ty = threadIdx.y;
    unsigned int gx = blockIdx.x * TILE_SIZE + tx;
    unsigned int gy = blockIdx.y * TILE_SIZE + ty;
    if (gx >= width || gy >= height)
        return;

    // Load shared memory
    int tile_num = (width + TILE_SIZE - ) / TILE_SIZE;
    float sum = ;
    for (int i = ; i < tile_num; ++i){
        int bound = min(width, TILE_SIZE);
        for (int j = tx; j < bound; j += blockDim.x){
            tile_A[ty][j] = A[gy * width + i * bound + j];
        }
        for (int j = ty; j < bound; j += blockDim.y){
            tile_B[j][tx] = B[(i * bound + j) * width + gx];
        }
        //Synchronize to make sure the sub-matrices are loaded before starting the computation
        __syncthreads();

        for (int j = ; j < bound; ++j){
            sum += tile_A[ty][j] * tile_B[j][tx];
        }
        //Synchronize to make sure that the preceding computation is done before loading two new
        //sub-matrices of M and N in the next iteration
        __syncthreads();
    }
    C[gy*width + gx] = sum;
} 

void constantInit(float *data, int size, float val){
    for (int i = ; i < size; ++i){
        data[i] = val;
    }
} 

void matrixMul(){
    int dev_id = ;
    cudaSetDevice(dev_id); 

    // Allocate host memory for matrices A and B
    int width = ;
    int height = ;
    unsigned int size = width * height;
    unsigned int mem_size = sizeof(float)* size;
    float *h_A = (float *)malloc(mem_size);
    float *h_B = (float *)malloc(mem_size);
    float *h_C = (float *)malloc(mem_size); 

    // Initialize host memory
    const float valB = 0.01f;
    constantInit(h_A, size, 1.0f);
    constantInit(h_B, size, valB); 

    // Allocate device memory
    float *d_A, *d_B, *d_C;
    cudaMalloc((void **)&d_A, mem_size);
    cudaMalloc((void **)&d_B, mem_size);
    cudaMalloc((void **)&d_C, mem_size); 

    // Memcpy
    cudaMemcpy(d_A, h_A, mem_size, cudaMemcpyHostToDevice);
    cudaMemcpy(d_B, h_B, mem_size, cudaMemcpyHostToDevice); 

    // Config dim
    dim3 block(TILE_SIZE, TILE_SIZE);
    dim3 grid((width + block.x - ) / block.x, (height + block.y - ) / block.y);
    matrixMulKernel <<<grid, block >>>(d_C, d_A, d_B, width, height); 

    // Memcpy device to host
    cudaMemcpy(h_C, d_C, mem_size, cudaMemcpyDeviceToHost); 

    // Check
    printf("Checking computed result for correctness: ");
    bool correct = true;
    // test relative error by the formula // |<x, y>_cpu - <x,y>_gpu|/<|x|, |y|> < eps
    double eps = .e-;
    // machine zero
    for (int i = ; i < (int)(width * height); i++) {
        double abs_err = fabs(h_C[i] - (width * valB));
        double dot_length = width;
        double abs_val = fabs(h_C[i]);
        double rel_err = abs_err / abs_val / dot_length;
        if (abs_err > eps) {
            printf("Error! Matrix[%05d]=%.8f, ref=%.8f error term is > %E\n", i, h_C[i], (float)(width*height), eps);
            correct = false;
        }
    }
    printf("%s\n", correct ? "Result = PASS" : "Result = FAIL");
}

合并访存：tile_A按行存储，tile_B按列存储，sum=row_tile_A * row_tile_B

__global__ void matrixMulKernel(float *C, float *A, float *B, int width, int height){
    __shared__ float tile_A[TILE_SIZE][TILE_SIZE];
    __shared__ float tile_B[TILE_SIZE][TILE_SIZE];
    unsigned int tx = threadIdx.x;
    unsigned int ty = threadIdx.y;
    unsigned int gx = blockIdx.x * TILE_SIZE + tx;
    unsigned int gy = blockIdx.y * TILE_SIZE + ty;
    if (gx >= width || gy >= height)
        return;

    // Load shared memory
    int tile_num = (width + TILE_SIZE - ) / TILE_SIZE;
    float sum = ;
    for (int i = ; i < tile_num; ++i){
        tile_A[tx][ty] = A[gy * width + i * TILE_SIZE + tx];
        tile_B[ty][tx] = B[(i * TILE_SIZE + ty) * width + gx];
        //Synchronize to make sure the sub-matrices are loaded before starting the computation
        __syncthreads();

        for (int j = ; j < TILE_SIZE; ++j){
            sum += tile_A[j][ty] * tile_B[j][tx];
        }
        //Synchronize to make sure that the preceding computation is done before loading two new
        //sub-matrices of M and N in the next iteration
        __syncthreads();
    }
    C[gy*width + gx] = sum;
}