burnside+polya 整理

先定义几个含义和符号：
起始状态/方法/位置/元素/：以染色为例，起始状态是所有的染色方案，方法是以起始状态所有染色方案为基准转变为新的染色情景的操作（如旋转），位置则必须是没有任何染色效果的抽象空间，元素则是各种颜色
循环： 在方法作用下，元素在位置上形成一个首尾相接的环（且定义这些位置是等价的）
迹： 在方法作用下，循环所遍及到的所有位置的集合
等价关系：一个置换集合G，如果一个置换方法能把其中一个方案映射到另一个方案，则二者是等价的
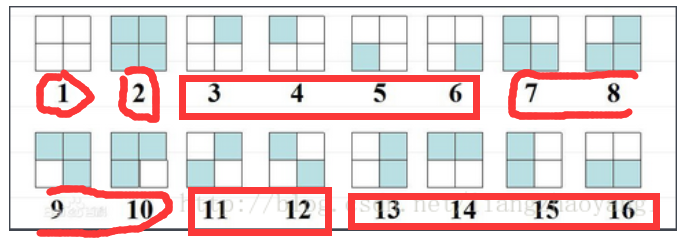
等价类： 满足等价关系的方案属于同一等价类，如：这里有6个等价类

C(pi)：表示pi方法形成循环的个数
循环的阶：循环中元素个数
Ck(pi)：表示pi中k阶循环个数
如：p1=(154)(2)(3)
C(p1)=3,C1(p1)=1,C2(p1)=0,C3(p1)=2
-------------------------------------------------
C(fk)：对象是“所有染色方案（且将每种方案效果合并起来）”
           对于每个染色方案 循环阶为1的fk方法的个数的总和 （即fk方法使所有染色方案哪些位置元素保持不变）
C'(fk)：对象是“位置”
            fk方法下的循环个数
Zk: k不动置换类 {p|p属于G，p(k)=k}，且Zk是G的子群 （使k位置元素不变的所有方法，|Zk|也叫k的稳定化子数）-->>这东西的存在其实就是哲学里的，”先抓一个定住，看其他的怎么变化“中的使之定住稳定住的东西
Ek：等价类 {a1(=k),a2,...,al},G中总存在pi，pi(a1)=ai(i=1,2,..l) （使这几个位置是等价的所有方法，|Ek|也叫k的轨道大小）
|Zk|*|Ek|=|G|: 轨道-稳定集定理：k的轨道大小*k的稳定化子数=总的变换个数 （G中所有的方法按k的轨道分类，对于每一个轨道来说，在这个轨道上的方法数为Zk,而每个轨道方法数一定相等。（由拉格朗日定理，Zk是子群就满足被整除的性质）
（注意这里”方法“不能跟”元素“这两个概念混在一起，方法是指对同一位置上“任意元素”都有相同效果，所以不要老纠结于元素的变化）
|H|整除|G|：拉格朗日定理。其中H是有限群G的子群（H的陪集要么重叠要么不相交，H的所有陪集的并等于G）
陪集： H为G的子群，对任意G中a，aH为陪集
位置方法转化定理：sgma(k=1~n)|Zk|=sgma(k=1~|G|)C(fk) （这里仅仅就是转换角度，将研究对象从位置k上的所有方法转变为方法fk对应的所有位置，最后求和还是一个东西，画张图就能明白）

burnside引理:
我们现在给出n个位置，那么根据等价类定义，有些位置上的等价类是相同的，Ei=Ej=Ek
我们要求不同的等价类个数，那么实际枚举位置k(1..n)可以想成对应的Ek为答案的贡献(1/|Ek|)
即 L=sgma(k=1~n)(1/|Ek|) //再用|Zk|*|Ek|=|G|: 轨道-稳定集定理进行变形，有
=(1/|G|)sgma(k=1~n)(|Zk|) //再用位置方法转化定理
=(1/|G|)sgma(k=1~|G|)C(fk)

但是，如对n个位置用m种颜色染色问题：
利用Burnside引理要首先列出所有n^m种可能的染色方案，然后找出在每个置换下保持不变的方法数。
显然当m或n很大的时候，操作会非常繁琐。 这时就需要用到polya定理。

polya定理：
它是抛弃起始状态（染色方案）这种观念而存在的定理（因为循环的迹上每个元素的选取是等价的，最后只要直接乘元素个数就行）
它而是将注意力完全放在抽象位置上，用C'(fk)操作，每个循环的迹有m种选择颜色的权利，所以m^(C'(fk))就是fk方法下不重复的染色图像个数（即等价类个数）
C(fk)=m^(C'(fk)) 两者其实都代表fk方法下等价类个数(这两者间直接证明基本上是不可能的，别妄想了），那么：
在所有方法下的等价类个数的总和除以方法数=在所有方法下的等价类个数
L=(1/|G|)sgma(k=1~|G|)m^(C'(fk))