go context

Context 使用原则

1、不要把Context放在结构体中，要以参数的方式传递

2、以Context作为参数的函数方法，应该把Context作为第一个参数，放在第一位。

3、给一个函数方法传递Context的时候，不要传递nil，如果不知道传递什么，就使用context.TODO

4、Context的Value相关方法应该传递必须的数据，不要什么数据都使用这个传递

5、Context是线程安全的，可以放心的在多个goroutine中传递

context取值

package main

import (
	"context"
	"fmt"
)

func process(ctx context.Context) {
	ret,ok := ctx.Value("trace_id").(int)
	if !ok {
		ret = 21342423
	}

	fmt.Printf("ret:%d\n", ret)

	s , _ := ctx.Value("session").(string)
	fmt.Printf("session:%s\n", s)
}

func main() {
	ctx := context.WithValue(context.Background(), "trace_id", 13483434)
	ctx = context.WithValue(ctx, "session", "sdlkfjkaslfsalfsafjalskfj")
	process(ctx)
}

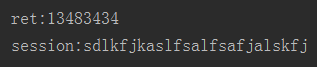
结果

withcancel

package main

import (
	"context"
	"fmt"
	"time"
)

func gen(ctx context.Context) <-chan int {
	dst := make(chan int)
	n := 1
	go func() {
		for {
			select {
			case <-ctx.Done():
				fmt.Println("i exited")
				return // returning not to leak the goroutine
			case dst <- n:
				n++
			}
		}
	}()
	return dst
}

func test() {
	// gen generates integers in a separate goroutine and
	// sends them to the returned channel.
	// The callers of gen need to cancel the context once
	// they are done consuming generated integers not to leak
	// the internal goroutine started by gen.
	ctx, cancel := context.WithCancel(context.Background())
	defer cancel() // cancel when we are finished consuming integers
	intChan := gen(ctx)
	for n := range intChan {
		fmt.Println(n)
		if n == 5 {
			break
		}
	}
}
func main() {
	test()
	time.Sleep(time.Hour)
}

WithDeadline

package main

import (
	"context"
	"fmt"
	"time"
)

func main() {
	d := time.Now().Add(50 * time.Millisecond)
	ctx, cancel := context.WithDeadline(context.Background(), d)

	// Even though ctx will be expired, it is good practice to call its
	// cancelation function in any case. Failure to do so may keep the
	// context and its parent alive longer than necessary.
	defer cancel()

	select {
	case <-time.After(1 * time.Second):
		fmt.Println("overslept")
	case <-ctx.Done():
		fmt.Println(ctx.Err())
	}

}