洛谷P2822 组合数问题

输入输出样例

输入样例#1：

1 2
3 3

输出样例#1：

1

输入样例#2：

2 5
4 5
6 7

输出样例#2：

0
7

说明

【样例1说明】

在所有可能的情况中，只有C_2^1 = 2C21​=2是2的倍数。

【子任务】

---

题目非常的长，但是意思很简单，就是求杨辉三角i行j列中能被k整除的数

因为组合数的意义其实就是杨辉三角（不懂得可以百度一下）好吧我接下来说一说

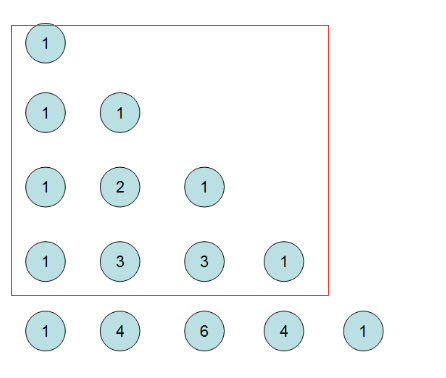
如图应该很明显了，但是对于OI来说的话可能放到左边用数组表示更加直观，顺便一提，最上方也可以加一个1，如图

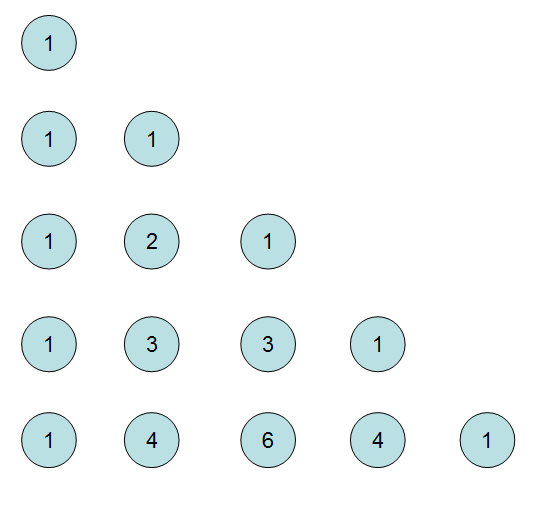
求第i行第j列中被k整除的数的个数如下

我们可以先将杨辉三角打印出来，当然这里可以优化一下，将杨辉三角中能被k整除的数直接标为0

for(int i=;i<=;i++) c[i][]=;
    for(int i=;i<=;i++)
        for(int j=;j<=;j++)
        {
            c[i][j]=(c[i-][j]+c[i-][j-])%k;
        }

我们设f[i][j]为第i行第j列之前的数中能被f整除的数，则f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+(c[i][j]==0)（注意这里(c[i][j]==0)是个判断，为了好写就加上了）

那么我们注意到当i==j时，f[i][j-1]是空的，也就是少一个f[i][i]的值，所以要在j=i时加上一个f[i][i]

核心代码如下：

 for(int i=;i<=;i++)
    {
        for(int j=;j<=i;j++)
        {
            f[i][j]=f[i-][j]+f[i][j-]-f[i-][j-];
            if(c[i][j]==)f[i][j]++;
        }
        f[i][i+]=f[i][i];//这里要到下一个i才会用到，所以在最后加
    }

那么完整版的ak代码经过修改组合就出来了：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<iomanip>
using namespace std;
int n,m,t,k,c[][],f[][];
int main()
{
    cin>>t>>k;
    for(int i=;i<=;i++) c[i][]=;
    for(int i=;i<=;i++)
        for(int j=;j<=;j++)
        {
            c[i][j]=(c[i-][j]+c[i-][j-])%k;
        }
    for(int i=;i<=;i++)
    {
        for(int j=;j<=i;j++)
        {
            f[i][j]=f[i-][j]+f[i][j-]-f[i-][j-];
            if(c[i][j]==)f[i][j]++;
        }
        f[i][i+]=f[i][i];
    }
    for(int i=;i<=t;i++)
    {
        cin>>n>>m;
        if(m>n)m=n;
        cout<<f[n][m]<<endl;;
    }
    return ;
}

特别鸣谢：hmr大佬，感谢大佬亲身讲解

大佬博客 https://www.cnblogs.com/hanruyun/