noip模拟题 2017.10.28 -kmp -Tarjan -鬼畜的优化

---

　　题目大意 给定A串，选择A串的前l_B个字符作为B串，再在B串后增加一个字符，问最长的相等的A串前缀和B串的后缀。

Solution 1(KMP)

　　用1个奇怪的字符连接A串和B串，再用KMP求最长公共前后缀。

Solution 2(Hash)

　　hash A串的前缀和B的后缀，然后for去比较，取最大的相等的一个

---

---

　　题目大意 找出图上所有点，当它被删掉后使得1和n不连通。

　　因为这个点删掉后能够使1和n不在同一个联通块内，所以这个点一定是割点。

　　但是不是所有的割点都合法。当这个点被删掉后，如何判断1和n是否在同一联通块中？

　　考虑Tarjan，在Tarjan造出的dfs树上，枚举每个割点(除了点1和点n)

　　假设当前枚举的割点为点i，首先考虑是否点n在点i的子树中，如果不在，说明删掉点i后，1和n一定连通，

　　现在考虑点n在点i的子树中，但是否存在反祖边使得点n和点1所在联通块连通。

　　这个根据Tarjan的过程中记录的深度优先值和连向的最早的祖先的值可以很容易得到想到下面一个方法

　　　　枚举点i的所有子树，判断点n是否在这中间，如果在，再判断那个点的反祖边有没有连向点i的祖先。

Code

 #include <iostream>
 #include <fstream>
 #include <sstream>
 #include <algorithm>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <cassert>
 #include <cmath>
 #include <cctype>
 #include <ctime>
 #include <vector>
 #include <bitset>
 #include <stack>
 #include <queue>
 #include <map>
 #include <set>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;
 typedef bool boolean;
 typedef pair<int, int> pii;
 #define smin(_a, _b) _a = min(_a, _b)
 #define smax(_a, _b) _a = max(_a, _b)
 #define fi first
 #define sc second
 
 template<typename T>
 inline boolean readInteger(T& u) {
     static char x = ;
     int flag = ;
     if(x == -)
         return false;
     while(!isdigit(x = getchar()) && x != '-' && x != -);
     if(x == -)
         return false;
     if(x == '-')
         flag = -, x = getchar();
     for(u = x - ''; isdigit(x = getchar()); u = u *  + x - '');
     u *= flag;
     return true;
 }
 
 const int N = 2e5 + ;
 const int M = 4e5 + ;
 
 typedef class Edge {
     public:
         int end;
         int next;
 
         Edge(int end = , int next = ):end(end), next(next) {        }
 }Edge;
 
 typedef class MapManager {
     public:
         int ce;
         int h[N];
         Edge edge[M << ];
 
         MapManager() {        }
         MapManager(int n):ce() {
             memset(h, , sizeof(int) * (n + ));
         }
 
         void addEdge(int u, int v) {
             edge[++ce] = Edge(v, h[u]);
             h[u] = ce;
         }
 
         void addDoubleEdge(int u, int v) {
             addEdge(u, v);
             addEdge(v, u);
         }
 
         int start(int node) {
             return h[node];
         }
 
         Edge& operator [] (int pos) {
             return edge[pos];
         }
 }MapManager;
 
 int n, m;
 MapManager g;
 
 inline void init() {
     readInteger(n);
     readInteger(m);
     g = MapManager(n);
     for(int i = , u, v; i <= m; i++) {
         readInteger(u);
         readInteger(v);
         g.addDoubleEdge(u, v);
     }
 }
 
 int cnt;
 int brunch[N];
 int dfn[N], ef[N];
 boolean exists[N];
 void tarjan(int node, int last) {
     brunch[node] = ;
     dfn[node] = ef[node] = ++cnt;
     for(int i = g.start(node); i; i = g[i].next) {
         int& e = g[i].end;
         if(e == last)    continue;
         if(brunch[e] == -) {
             tarjan(e, node);
             brunch[node]++;
             smin(ef[node], ef[e]);
             exists[node] = exists[node] || exists[e];
         } else {
             smin(ef[node], dfn[e]);
         }
     }
 //    cerr << node << " " << dfn[node] << " " << ef[node] << endl;
 }
 
 boolean check(int node) {
     for(int i = g.start(node); i; i = g[i].next)
         if(dfn[g[i].end] > dfn[node] && ef[g[i].end] < dfn[node] && exists[g[i].end])
             return false;
     return true;
 }
 
 int top;
 int lis[N];
 inline void solve() {
     cnt = ;
     memset(brunch, -, sizeof(int) * (n + ));
     memset(exists, false, sizeof(int) * (n + ));
     exists[n] = true;
     tarjan(, );
     top = ;
     for(int i = ; i < n; i++)
         if(brunch[i] >  && check(i) && exists[i])
             lis[top++] = i;
     printf("%d\n", top);
     for(int i = ; i < top; i++)
         printf("%d ", lis[i]);
     putchar('\n');
 }
 
 int T;
 int main() {
     freopen("home.in", "r", stdin);
     freopen("home.out", "w", stdout);
     readInteger(T);
     while(T--) {
         init();
         solve();
     }
     return ;
 }

---

---

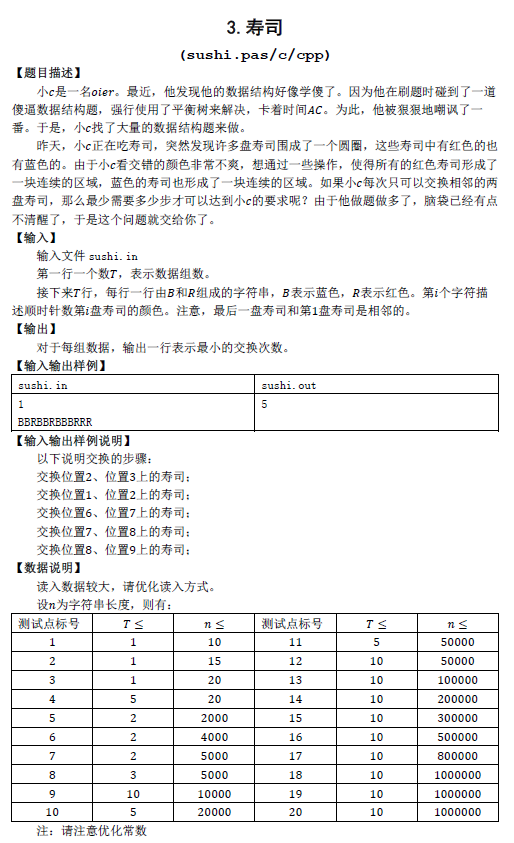
　　题目大意 有n个球排成了一个环，球的颜色不是红色就是蓝色，每次操作可以交换相邻的两个球，问最少多少次操作可以使得所有同一种颜色的球都挨在一起。

　　显然是需要枚举的。

　　所以考虑枚举中间的位置，然后贪心地把一种颜色往两端塞。

　　然后会发现有一定单调性，故用两个队列维护一下扔左边的和扔右边的的球。

Code

 #include <iostream>
 #include <fstream>
 #include <sstream>
 #include <algorithm>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <cassert>
 #include <cmath>
 #include <cctype>
 #include <ctime>
 #include <vector>
 #include <bitset>
 #include <stack>
 #include <queue>
 #include <map>
 #include <set>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;
 typedef bool boolean;
 typedef pair<int, int> pii;
 #define ll long long
 #define smin(_a, _b) _a = min(_a, _b)
 #define smax(_a, _b) _a = max(_a, _b)
 #define fi first
 #define sc second
 const signed ll llf = (~0ll) >> ;
 template<typename T>
 inline boolean readInteger(T& u) {
     static char x = ;
     int flag = ;
     if(x == -)
         return false;
     while(!isdigit(x = getchar()) && x != '-' && x != -);
     if(x == -)
         return false;
     if(x == '-')
         flag = -, x = getchar();
     for(u = x - ''; isdigit(x = getchar()); u = u *  + x - '');
     u *= flag;
     return true;
 }
 
 const int N = 1e6 + ;
 
 int n;
 deque<int> ql, qr;
 char s[N];
 
 inline void init() {
     gets(s);
     n = strlen(s);
 }
 
 inline void solve() {
     ll res = , cmp = ;
     for(int i = ; i < n; i++)
         if(s[i] == 'R')
             cmp += i - (signed)qr.size(), qr.push_back(i);
     int p, d1, d2;
     while(!qr.empty()) {
         p = qr.back();
         d1 = p - (signed)qr.size() + ;
         d2 = n - (signed)ql.size() - p - ;
         if(d1 > d2)    qr.pop_back(), ql.push_front(p), cmp += d2 - d1;
         else break;
     }
     res = cmp;
 
     for(int i = , p, d1, d2; i < n; i++) {
         boolean flag = false;
         if(qr.front() < i) {
             ql.push_back(qr.front());
             qr.pop_front();
             flag = true;
         }
         if(!flag)    cmp += (signed)ql.size() - (signed)qr.size();
         while(!ql.empty()) {
             p = ql.front();
             d1 = (p - (i + (signed)qr.size()) % n + n) % n;
             d2 = ((i - (signed)ql.size() + n) % n - p + n) % n;
             if(d1 < d2)    ql.pop_front(), qr.push_back(p), cmp += d1 - d2;
             else break;
         }
         smin(res, cmp);
     }
     printf(Auto"\n", res);
     ql.clear();
     qr.clear();
 }
 
 int T;
 int main() {
     freopen("sushi.in", "r", stdin);
     freopen("sushi.out", "w", stdout);
     readInteger(T);
 //    gets(s);
     while(T--) {
         init();
         solve();
     }
     return ;
 }