Machine Learning 学习笔记2 - linear regression with one variable(单变量线性回归)

一、Model representation（模型表示）

1.1 训练集

由训练样例(training example)组成的集合就是训练集(training set), 如下图所示, 其中(x,y)是一个训练样例, (x(i),y(i))是第 i个训练样例.

1.2 假设函数

使用某种学习算法对训练集的数据进行训练, 我们可以得到假设函数(Hypothesis Function), 如下图所示. 在房价的例子中，假设函数就是一个房价关于房子面积的函数。有了这个假设函数之后, 给定一个房子的面积我们就可以预测它的价格了.

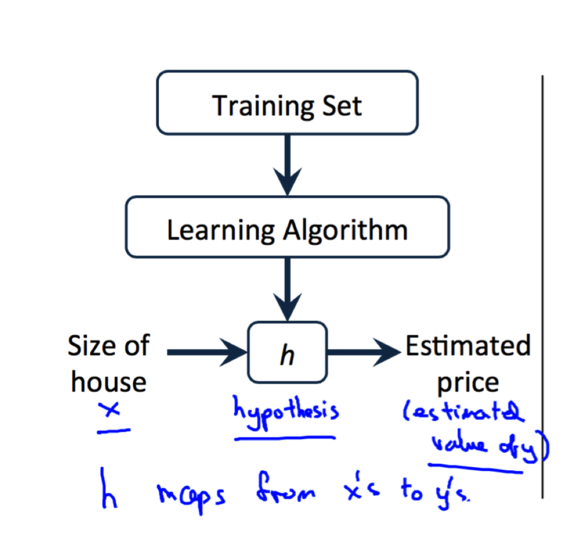  Hypothesis这个词或许在这里不是很恰当。但这是机器学习中使用的标准术语.

以上这个模型就叫做单变量的线性回归(Linear Regression with One Variable). (Linear regression with one variable = Univariate linear regression，univariate是one variable的装逼写法.)

二、Cost Function（代价函数）

2.1 什么是代价函数

只要我们知道了假设函数, 我们就可以进行预测了. 关键是, 假设函数中有两个未知的量θ0,θ1. 当选择不同的θ0和θ1时, 我们模型的效果肯定是不一样的.

如下图所示, 列举了三种不同的θ0和θ1下的假设函数.

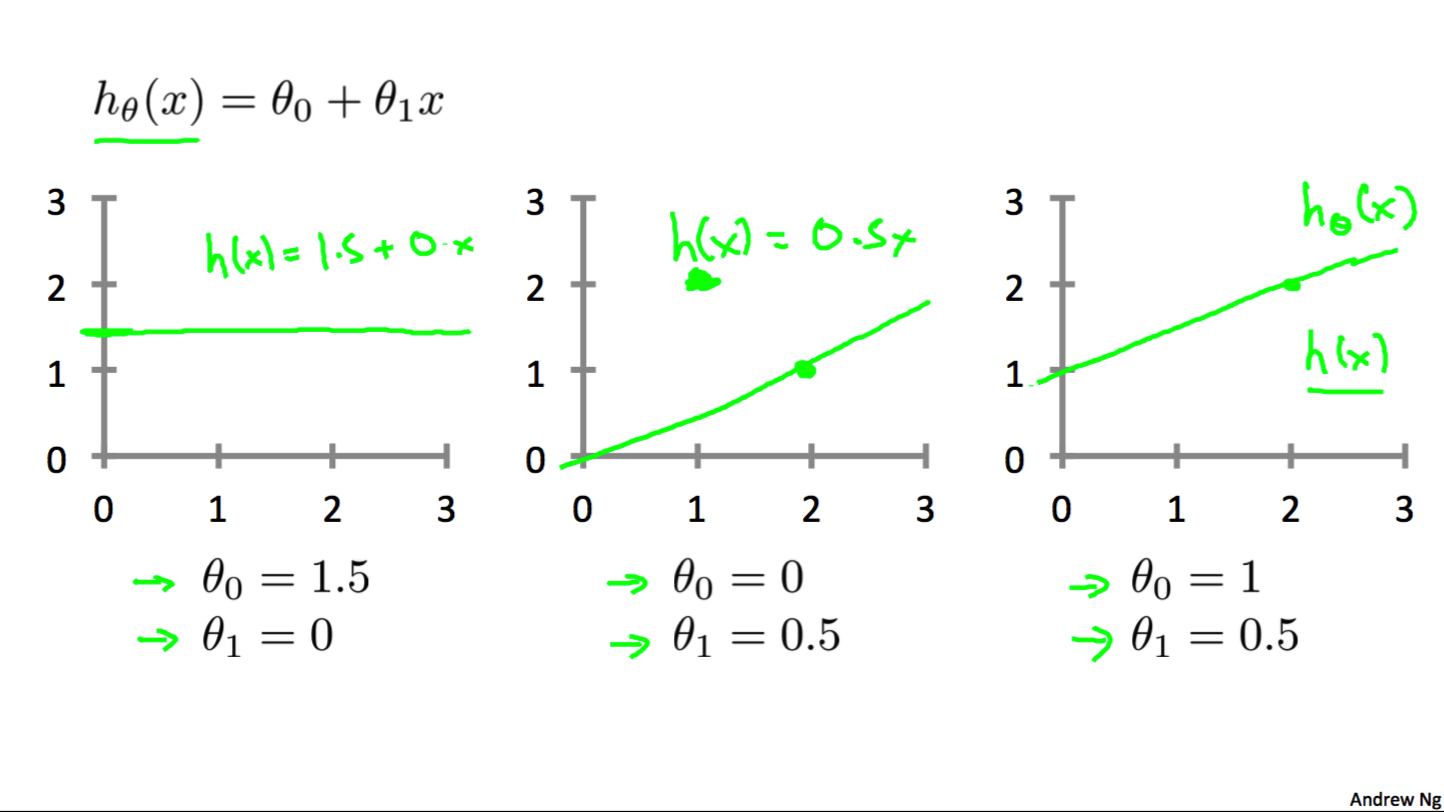
(其中的1/2只是为了后面计算的方便)我们记:

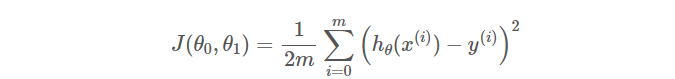
这样就得到了我们的代价函数(cost function), 也就是我们的优化目标, 我们想要代价函数最小:

代价函数也被称为平方误差函数(Squared error function）

2.2 代价函数与假设函数

2.2 代价函数与假设函数II

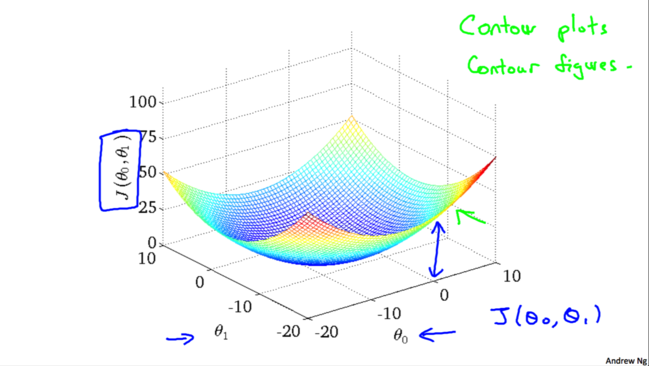
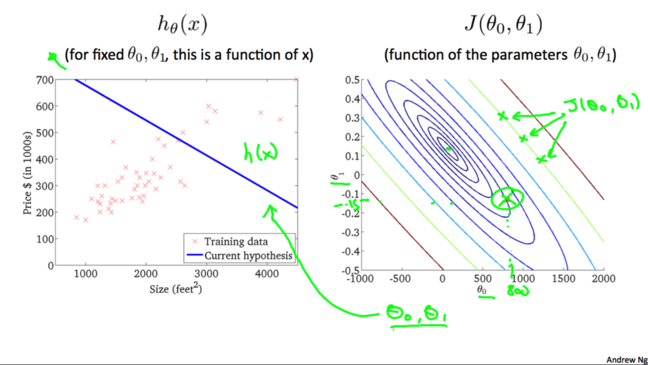
类似地：

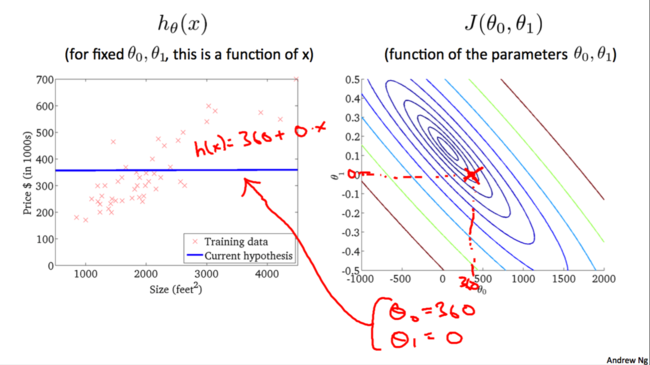
我们不断尝试直到找到一个最佳的hθ(x)hθ(x)。是否有特定的算法能帮助我们找到最佳的hθ(x)hθ(x)呢?

下面我们就要介绍这个算法-梯度下降算法.

三. 梯度下降算法

3.1 梯度下降

可以把梯度下降的过程想象成下山坡, 如果想要尽可能快的下坡, 应该每次都往坡度最大的方向下山.

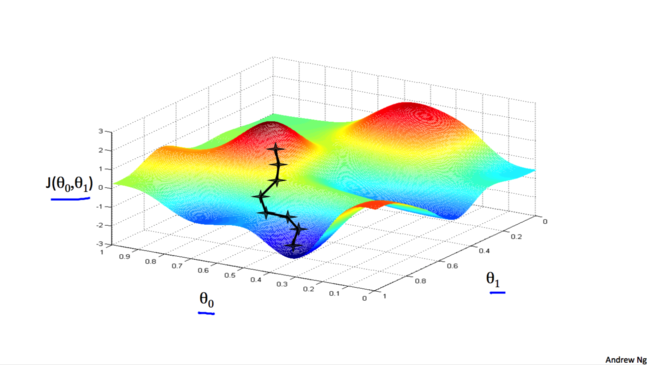
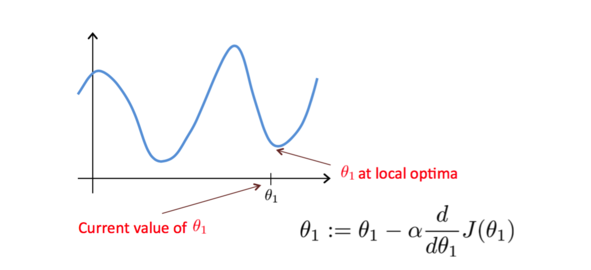
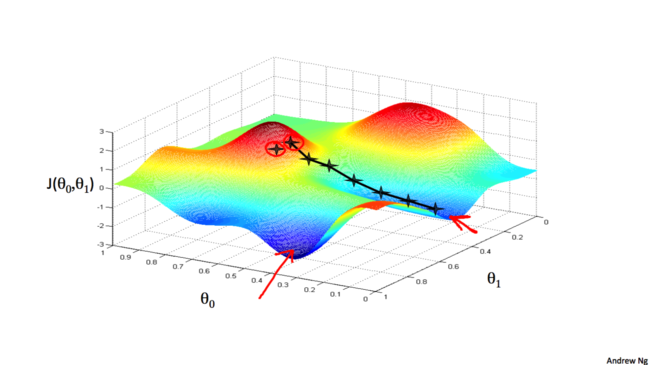
梯度下降算法得到的结果会受到初始状态的影响, 即当从不同的点开始时, 可能到达不同的局部极小值, 如下图:

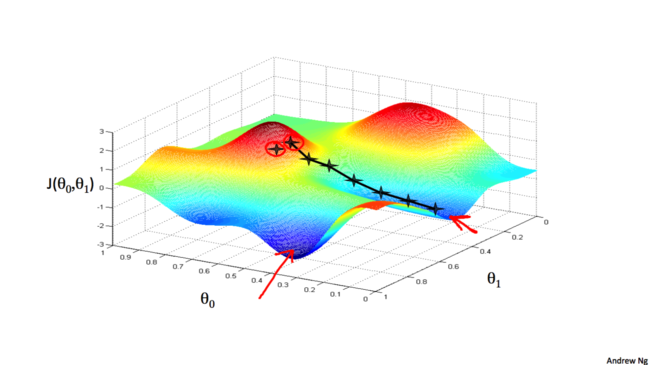
3.2 梯度和学习率

我们先来看看梯度下降算法的梯度是如何帮助我们找到最优解的. 为了研究问题的方便我们还是同样地令θ0θ0等于0，假设一开始选取的θ1θ1在最低点的右侧，此时的梯度(斜率)是一个正数。根据上面的算法更新θ1θ1的时候，它的值会减小, 即靠近最低点。

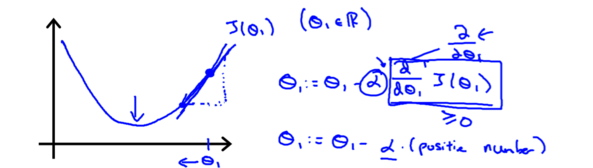
类似地假设一开始选取的θ1θ1在最低点的左侧，此时的梯度是一个负数，根据上面的算法更新θ1θ1的时候，它的值会增大，也会靠近最低点.

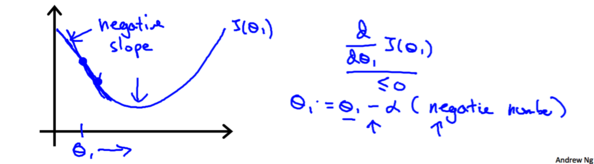
如果一开始选取的θ1θ1恰好在最适位置，那么更新θ1θ1时，它的值不会发生变化。

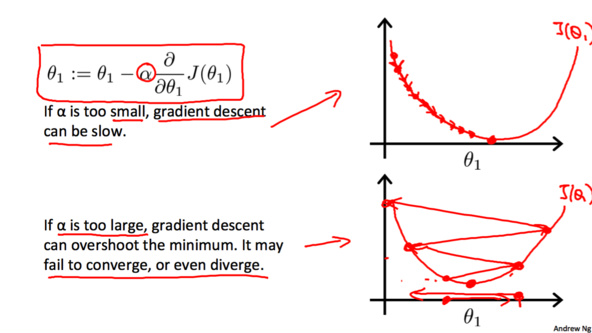
学习率α会影响梯度下降的幅度。如果α太小, θ的值每次会变化的很小，那么梯度下降就会非常慢；相反地，如果α过大，θ的值每次会变化会很大，有可能直接越过最低点，可能导致永远没法到达最低点。

由于随着越来越接近最低点, 相应的梯度(绝对值)也会逐渐减小，所以每次下降程度就会越来越小, 我们并不需要减小αα的值来减小下降程度。

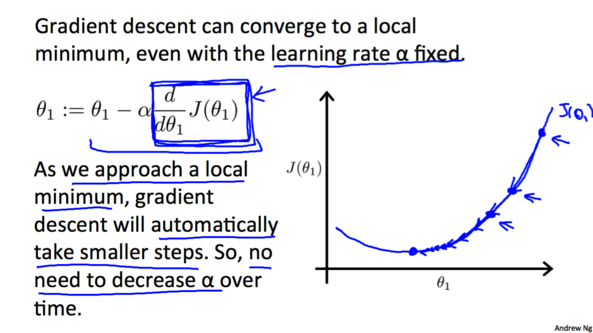
3.3 计算梯度

根据定义, 梯度也就是代价函数对每个θ的偏导:

由此得到了完整的梯度下降算法:

还记得这个图吗, 前面说了梯度下降算法得到的结果会受初始状态的影响, 即初始状态不同, 结果可能是不同的局部最低点.

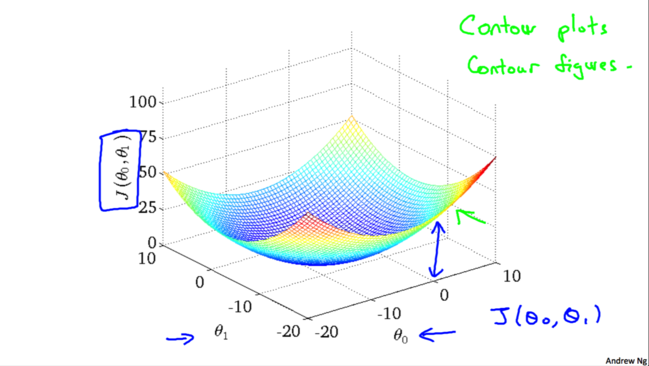
事实上，用于线性回归的代价函数总是一个凸函数(Convex Function)。这样的函数没有局部最优解，只有一个全局最优解。所以我们在使用梯度下降的时候，总会得到一个全局最优解。

下面我们来看一下梯度下降的运行过程：

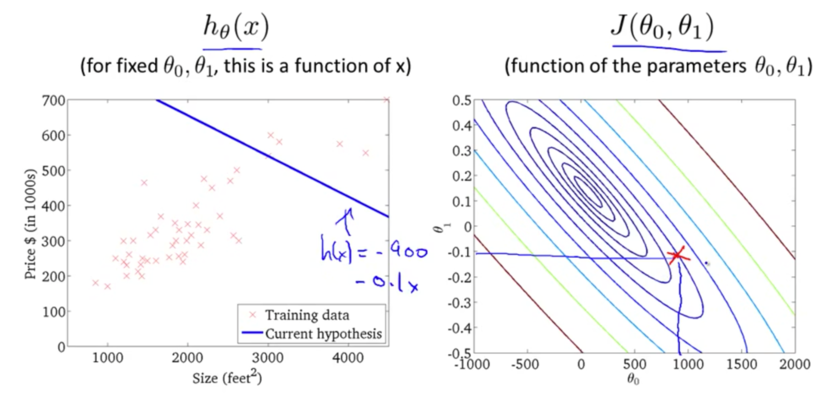
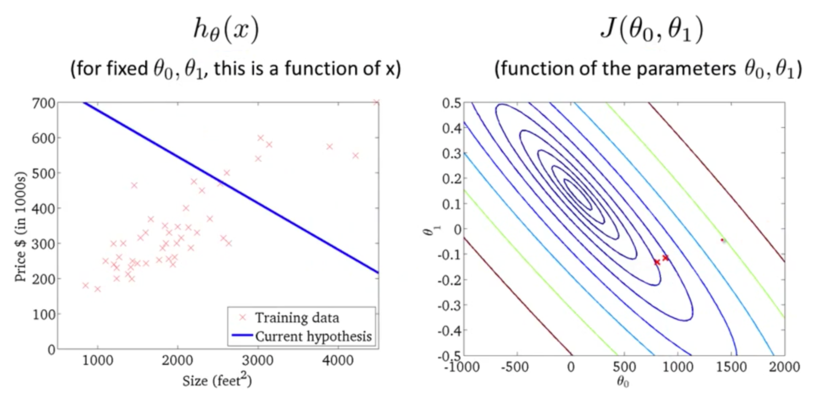
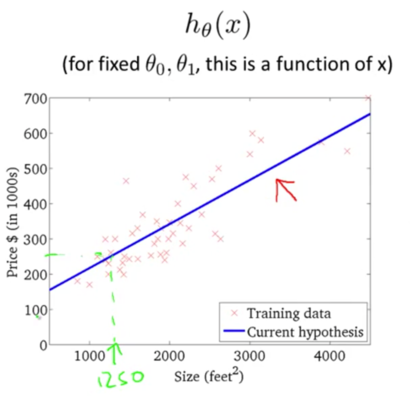
迭代多次后，我们得到了最优解。现在我们可以用最优解对应的假设函数来对房价进行预测了。例如一个1,250平方英尺的房子大概能卖到250k$，如下图所示：