Ex 6_5棋子放置问题_第八次作业

题目貌似有问题

(b)

子问题定义: 设maxValue[i][j]为棋盘的前i行中最后一行为i时第i行按照第j种放置方式放置时得到的最大覆盖值，comp[i][j]为第i种放置方式与第j种放置方式是否相容，value[i][j]为第i行按照第j种放置方式放置时覆盖整数的最大值，如此可以得到递归式。

递归关系: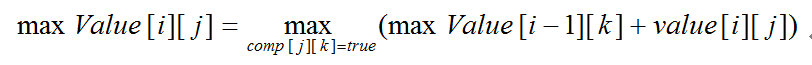

初值设定：

maxValue的行数为棋盘的行数加一，因此令maxValue[0][j]=0表示没有棋盘时值为0

求解顺序：

按从上到下，从左到右的次序求解maxValue的每一行的值，最终返回maxValue的最后一行的最大值即为最终解。

 package org.xiu68.ch6.ex8;

 public class Ex6_5 {

     public static void main(String[] args) {
         // TODO Auto-generated method stub
         int[][] chessBoard1=new int[][]{
             {1,2,3,4},
             {2,1,2,1}
         };
         maxChessBoard(chessBoard1);   

         int[][] chessBoard2=new int[][]{
             {0,1,0,1},
             {1,0,1,0},
             {1,2,1,2}
         };
         maxChessBoard(chessBoard2);

         //运行结果
         /*
          被棋子覆盖的整数总和最大为: 10
         被棋子覆盖的整数总和最大为: 8
         */

     }

     //chessBoard:棋盘
     public static void maxChessBoard(int[][] chessBoard){
         int TYPE=8;                        //每一行可以放置的棋的种类数
         int rows=chessBoard.length;        //棋盘的行
         int cols=4;                        //棋盘的列

         //comp[i][j]表示i、j两种放置模式是否相容，每行共8种放置方式
         boolean[][] comp=new boolean[][]{
             {true,true,true,true,true,true,true,true},
             {true,false,true,true,true,false,true,false},
             {true,true,false,true,true,true,false,true},
             {true,true,true,false,true,false,true,true},
             {true,true,true,true,false,true,false,false},
             {true,false,true,false,true,false,true,false},
             {true,true,false,true,false,true,false,false},
             {true,false,true,true,false,false,false,false}
         };

          //每行8种放置方式，method[i][j]表示某一行在第i种放置方式下的第j列是否放棋
          boolean[][] method=new boolean[][]{
              {false,false,false,false},
              {true,false,false,false},
              {false,true,false,false},
              {false,false,true,false},
              {false,false,false,true},
              {true,false,true,false},
              {false,true,false,true},
              {true,false,false,true}
          };    

         //max[i][j]表示前i行中最后一行为i时第i行按照第j种放置方式的最大值
         int[][] max=new int[rows+1][TYPE];
         for(int i=0;i<TYPE;i++)
             max[0][i]=0;                //最小子问题，初始化为0        

         //value[i][t]表示第i行按照第t种方式放棋得到的值
         int[][] value=new int[rows][TYPE];
         //初始化value数组
         for(int i=0;i<rows;i++){
             for(int t=0;t<TYPE;t++){

                 for(int j=0;j<cols;j++){
                     if(method[t][j]){        //第t种放置方式下第j列是否放棋
                         value[i][t]+=chessBoard[i][j];
                     }
                 }

             }
         }
         //求max数组
         for(int i=1;i<max.length;i++){
             for(int t=0;t<TYPE;t++){

                 max[i][t]=0;
                 for(int k=0;k<TYPE;k++){
                     if(!comp[t][k])        //t、k两种放置方式不相容
                         continue;
                     if(max[i-1][k]+value[i-1][t]>max[i][t])
                         max[i][t]=max[i-1][k]+value[i-1][t];
                 }

             }
         }

         //求max数组的最后一行的最大值即为最终解
         int maxValue=0;
         for(int i=0;i<TYPE;i++){
             if(max[max.length-1][i]>maxValue)
                 maxValue=max[max.length-1][i];
         }
         System.out.println("被棋子覆盖的整数总和最大为: "+maxValue);
     }

 }