奇怪吸引子---YuWang
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性、稳定性、吸引性。吸引子是一个数学概念,描写运动的收敛类型。它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出发的非定常流的所有轨道都趋于它,这样的集合有很复杂的几何结构。由于奇怪吸引子与混沌现象密不可分,深入了解吸引子集合的性质,可以揭示出混沌的规律。
这里会展示利用奇怪吸引子生成的艺术图像。奇怪吸引子通常含有三维或四维的数据,而图像是二维的,因此可以从不同的位面将奇怪吸引子投影到二维图像中。
原图及数学公式取自:
http://chaoticatmospheres.com/125670/1204030/gallery/strange-attractors

这里使用自己定义语法的脚本代码生成混沌图像,相关软件参见:YChaos生成混沌图像。如果你对数学生成图形图像感兴趣,欢迎加入QQ交流群: 367752815。
脚本代码:
[ScriptLines]
u=a*(j - i)
v=b*i - c*i*k
w=pow(E, i*j) - d*k
i=i+u*t
j=j+v*t
k=k+w*t
x=i
y=j [Variables]
a=10.000000
b=40.000000
c=2.000000
d=2.500000
i=1.000000
j=1.000000
k=1.000000
t=0.001000
混沌图像:

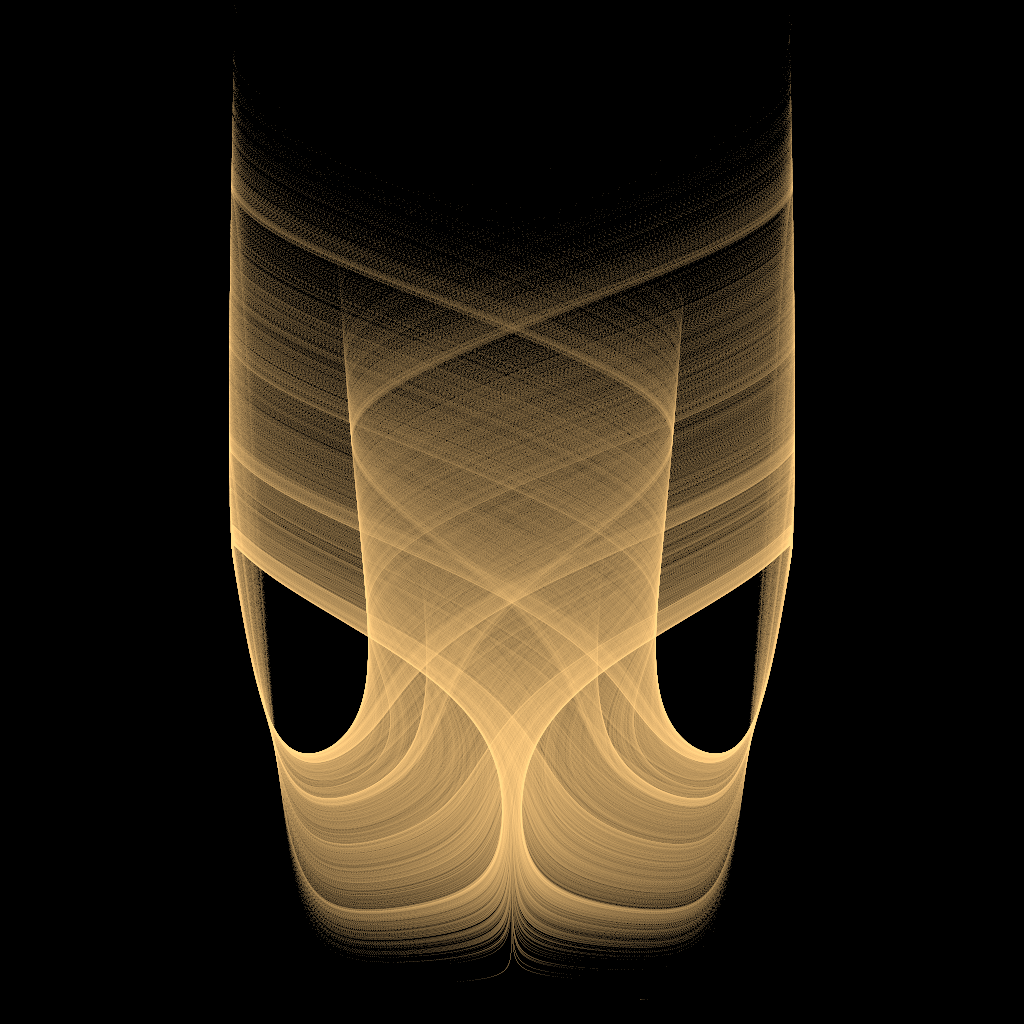
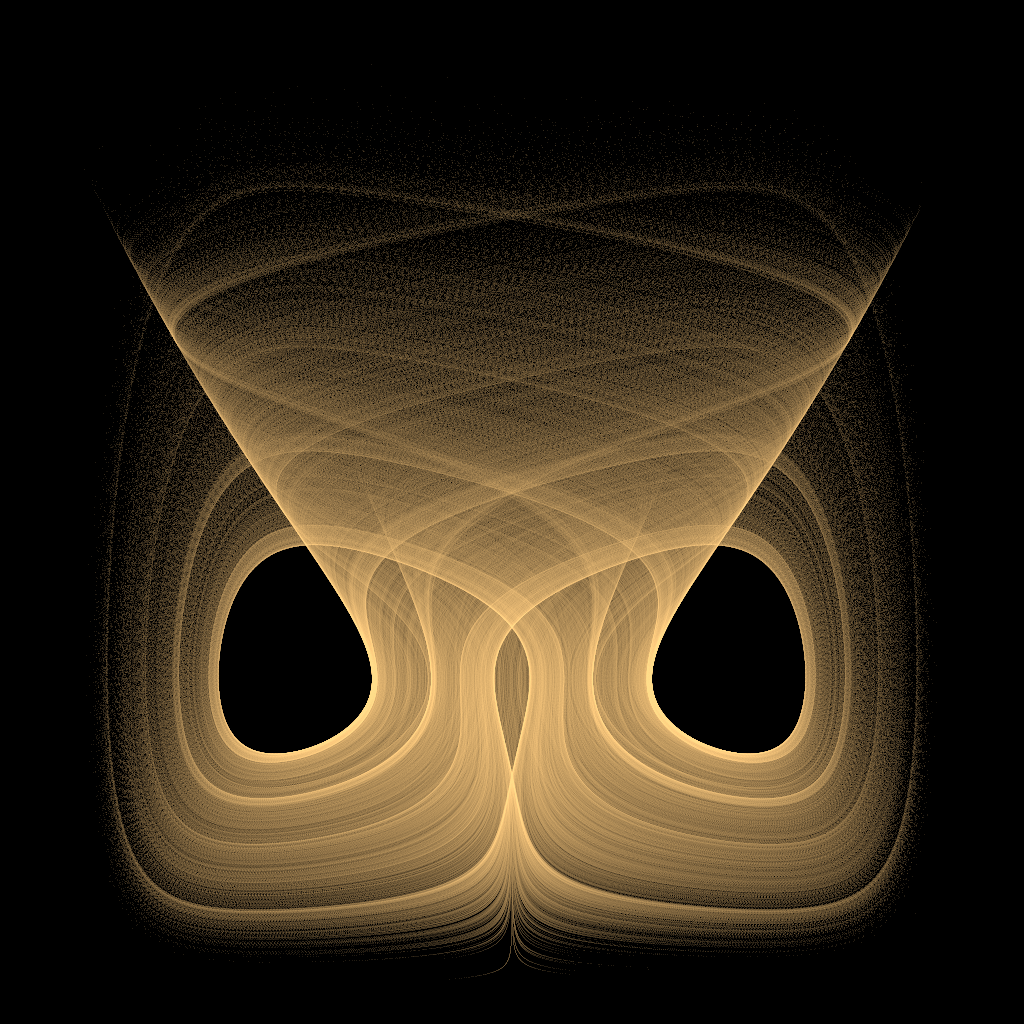

奇怪吸引子---YuWang的更多相关文章
- 奇怪吸引子---WimolBanlue
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WangSun
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---TreeScrollUnifiedChaoticSystem
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Thomas
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---ShimizuMorioka
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Sakarya
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Russler
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Rucklidge
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---RayleighBenard
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
随机推荐
- 20145225 《Java程序设计》第2周学习总结
20145225<Java程序设计> 第2周学习总结 教材学习内容总结 3.1.1Java的类型 分为基本类型(Primitive type)和类类型(Class type) 基本类型: ...
- 用Backbone.js创建一个联系人管理系统(一)
原文 Build a Contacts Manager Using Backbone.js: Part 1 在这个教程里我们将会使用Backbone.js,Underscore.js,JQuery创建 ...
- 校验两次密码一致的js代码
function checkpasswd(){ var passwd = document.getElementByIdx_x_x_xx_x('passwd').value; var repasswd ...
- Oracle一个中文汉字占用几个字节
Oracle 一个中文汉字 占用几个字节,要根据Oracle中字符集编码决定 查看oracle server端字符集 select userenv('language') from dual; 如 ...
- Linux-TFTP之用于网络远程安装
TFTP:Trival File Transfer Protocol,简单文件传输协议.是TCP/IP协议族中的一个用来在客户机与服务器之间进行简单文件传输的协议,提供不复杂.开销不大的文件传输服务. ...
- hdu 5101 n集合选2个不同集合数使和大于k
http://acm.hdu.edu.cn/showproblem.php?pid=5101 给n个集合,选择两个来自不同集合的数,加和大于k,问有多少种选择方案. 答案=从所有数中选择的两个加和大于 ...
- Zabbix3.0 自动微信报障
本来研究了一段时间短信报障的,但是短信报障需要手机运营商的设备支持,就没有继续下去. 正好发现微信公众号可以报障,完全可以代替短信报警的功能. 首先你需要一个微信公众号,实名认不认证没关系. http ...
- Spring Mobile 1.1.0.RC1 和 1.0.2 发布
Spring Mobile 1.1.0.RC1 发布了,该版本包含: 支持 Firefox OS 设备的检测 修复了使用 LiteDeviceDelegatingViewResolver 处理重定向和 ...
- Dynamic CRM 2013学习笔记(十七)JS读写各种类型字段方法及技巧
我们经常要对表单里各种类型的字段进行读取或赋值,下面列出各种类型的读写方法及注意事项: 1. lookup 类型 清空值 var state = Xrm.Page.getAttribute(" ...
- 深入理解java虚拟机【Java虚拟机垃圾收集器】
Java堆内存被划分为新生代和年老代两部分,新生代主要使用复制和标记-清除垃圾回收算法,年老代主要使用标记-整理垃圾回收算法,因此java虚拟中针对新生代和年老代分别提供了多种不同的垃圾收集器,JDK ...
