Java数组 —— 八大排序

（请观看本人博文——《详解 普通数组 —— Arrays类 与 浅克隆》）

在本人《数据结构与算法》专栏的讲解中，本人讲解了如何去实现数组的八大排序。

但是，在讲解的过程中，我们能够发现：这些几乎都和指针相关

同学们可能就会和本人一样，想到了Java中不存在指针的概念，

那么，该如何去实现呢？

本人在这里要提出的一点是：

虽然Java不存在指针，但是，Java处处都是指针。

这句话可能在本人的《Java SE》专栏的前期博文中大家经常能够看到。

那么，现在，本人就来讲解下在Java中，这八大排序该如何实现：

---

冒泡排序

时间复杂度：

O(n^2)

基本原理：

每一个数与它后面的数相比较，最终每一轮排完都会将未排序中最大（或最小）的数排在适当的位置

动态演示：



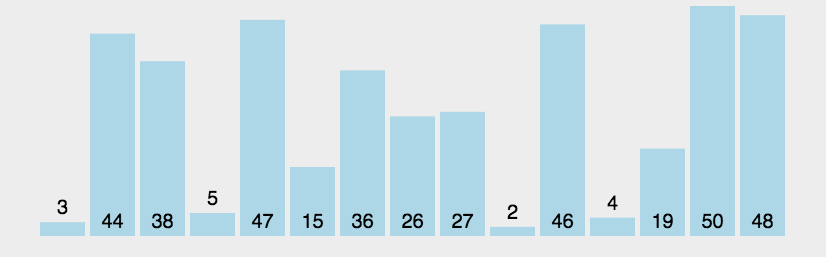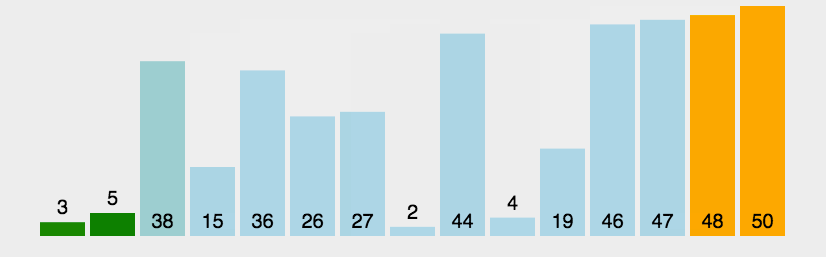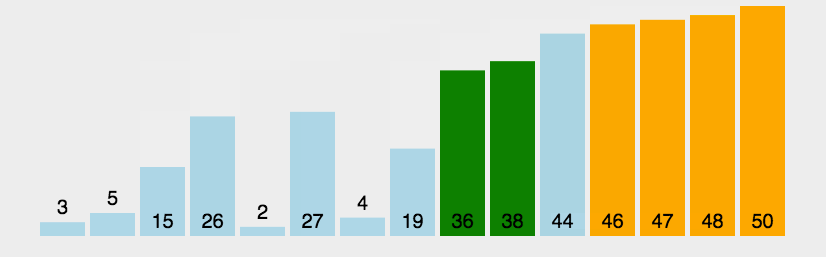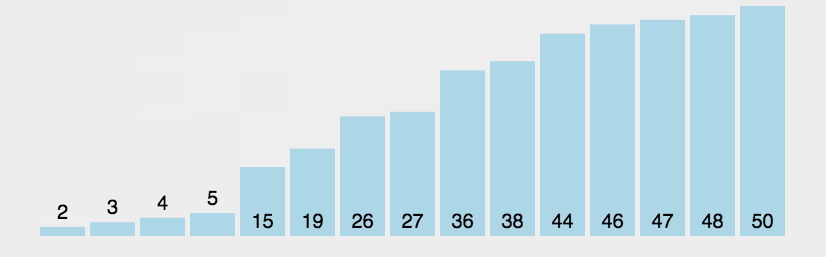
代码实现：

package aboutArraySort;

import java.util.Arrays;

public class BubbleSort {

	public static void main(String[] args) {
        int[] array = {37, 59, 43, -98, -17, 0};
        sort(array);
        System.out.println(Arrays.toString(array));
    }

    public static void sort(int[] array) {
        for (int i = array.length - 1; i > 0; i--) {
            for (int j = 0; j < i; j++) {
                if (array[j] > array[j+1]) {
                	swapValue(array, j, j+1);
                }
            }
        }
    }

    private static void swapValue(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

}

那么，本人来展示下运行结果：

---

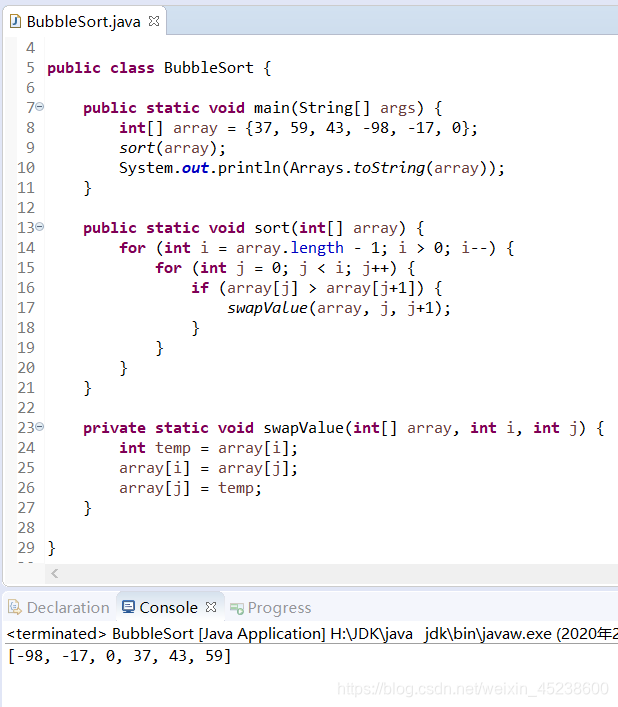
选择排序

时间复杂度：

O(n^2)

基本原理：

用未排序序列的第一个数和后面的所有数相比，

这样一轮下来，最大（或最小）的数就排到了相应的位置

经过最多（array.length - 1）轮后，整个数组就排好了序

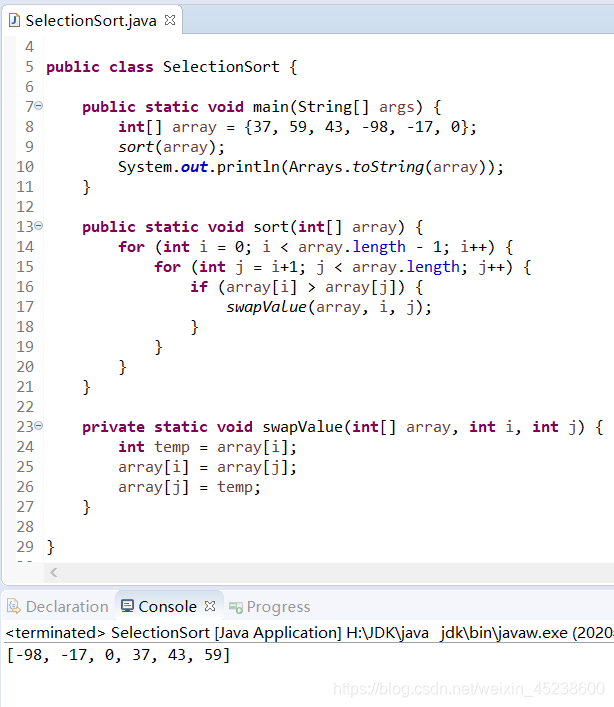
动态演示：



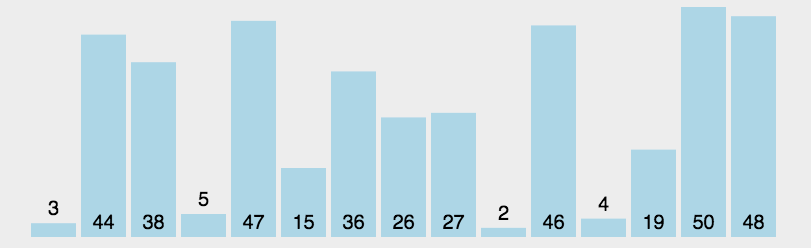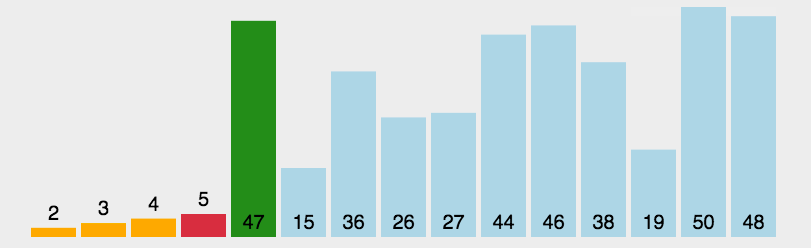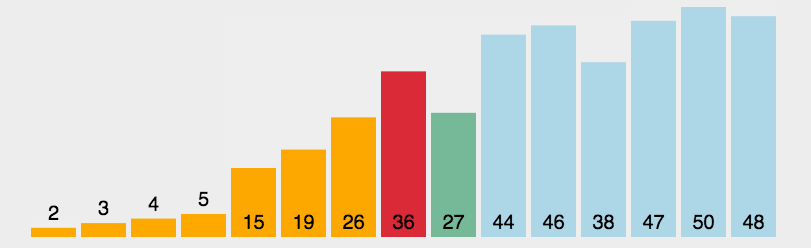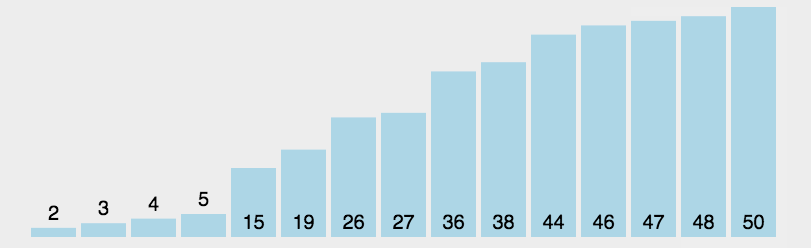
代码实现：

package aboutArraySort;

import java.util.Arrays;

public class SelectionSort {

	public static void main(String[] args) {
        int[] array = {37, 59, 43, -98, -17, 0};
        sort(array);
        System.out.println(Arrays.toString(array));
    }

    public static void sort(int[] array) {
        for (int i = 0; i < array.length - 1; i++) {
            for (int j = i+1; j < array.length; j++) {
                if (array[i] > array[j]) {
                	swapValue(array, i, j);
                }
            }
        }
    }

    private static void swapValue(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

}

那么，本人来展示下运行结果：

---

插入排序

时间复杂度：

O(n^2)

基本原理：

首先将原始数组分成两个数组容器（可通过下标来）

将原始数组的第一个数放在1号容器中，其余放在2号容器中

从2号容器中逐个取出，插在1号容器的适当位置

动态演示：

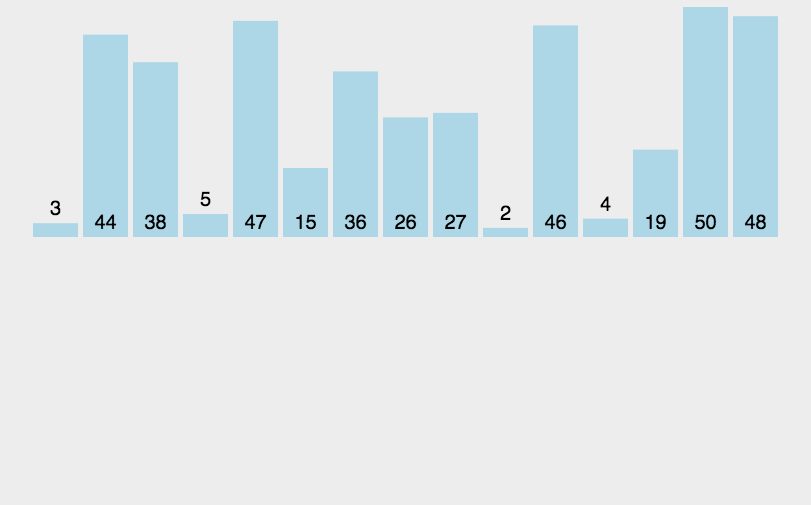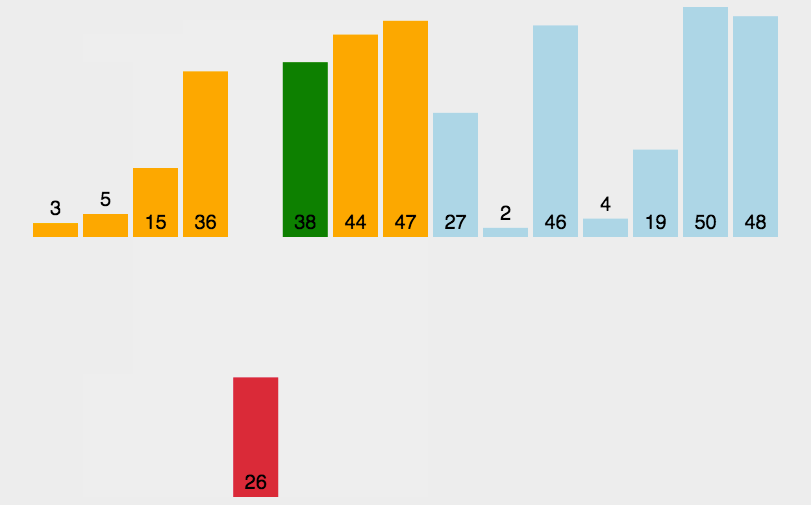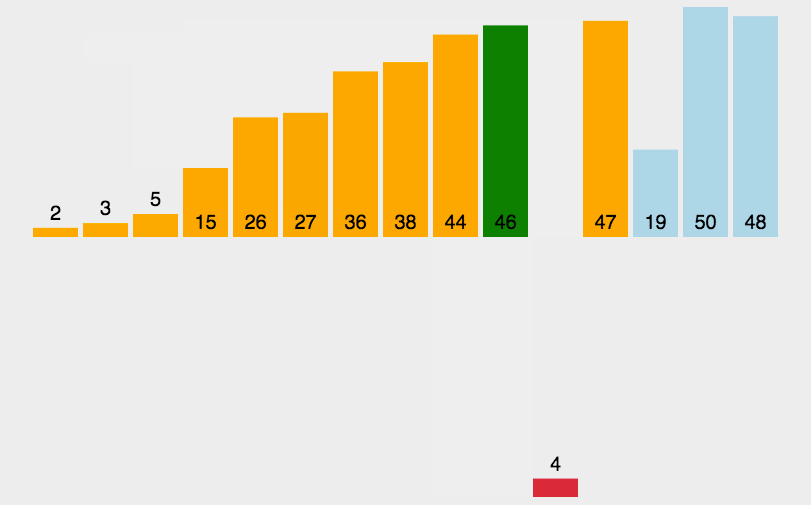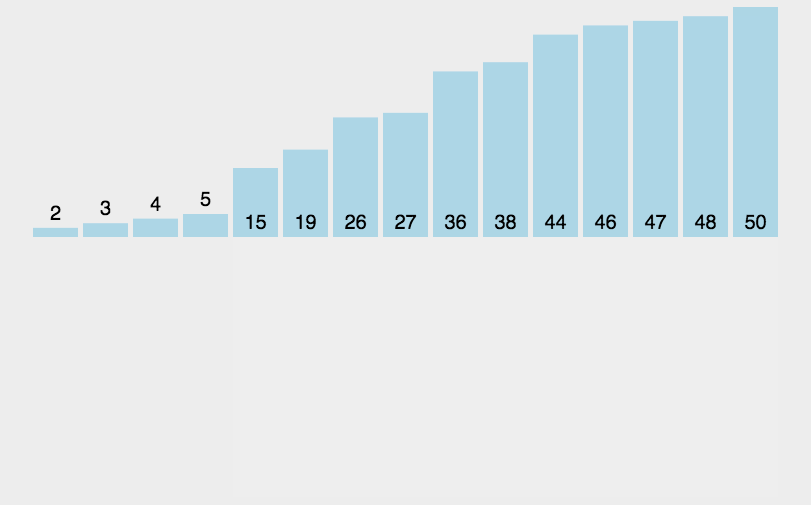
代码实现：

package aboutArraySort;

import java.util.Arrays;

public class InsertionSort {

	public static void main(String[] args) {
        int[] array = {37, 59, 43, -98, -17, 0};
        sort(array);
        System.out.println(Arrays.toString(array));
    }

	public static void sort(int[] array) {
        for (int i = 0; i < array.length; i++) {
            for (int j = i; j > 0; j--) {
                if (array[j-1] > array[j]) {
                	swapValue(array, j-1, j);
                }
            }
        }
    }

	private static void swapValue(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

}

那么，本人来展示下运行结果：

---

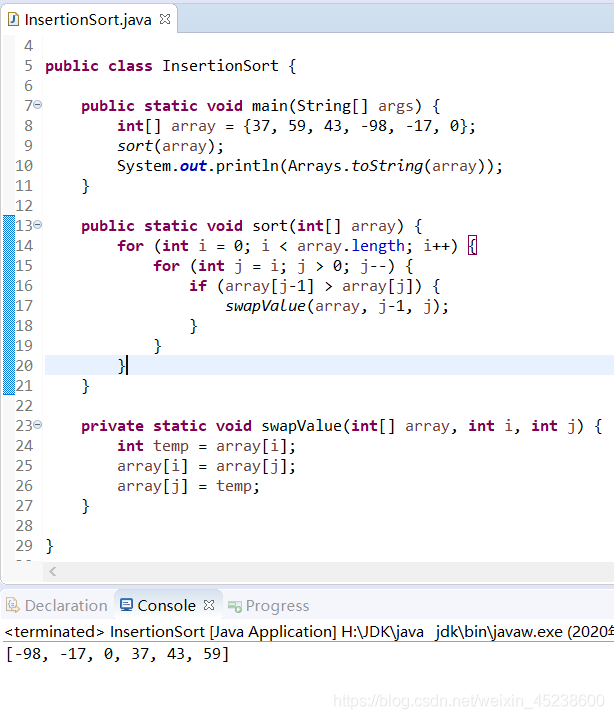
希尔排序

时间复杂度：

O(n^1.3)

基本原理：

先将原数组中的数据按照增量step分组

分出来的组按照插入排序进行排序

之后再对每个小组按照增量step/2分组

再对每个小组进行插入排序。

如此类推，直到增量step=1时，整个数组就排好序了

那么，看了上面的基本原理，我们就能知道 ：

增量step的选取十分关键

所以，在这里，本人就用了克努特序列来计算增量step。

所谓克努特序列，

就是按照：num = num*3 + 1的顺序排列的序列

例：1， 4， 13， 40， 121， 364 ... ...

由数学推导可得：用这种序列来进行希尔排序，效率极高。

动态演示：

代码实现：

package aboutArraySort;

import java.util.Arrays;

public class ShellSort {

	public static void main(String[] args) {
        int[] array = {37, 59, 43, -98, -17, 0};
        sort(array);
        System.out.println(Arrays.toString(array));
    }

	public static void sort(int[] array) {
        int maxStep = calculationStepLength(array.length);
        for (int step = maxStep; step > 0; step = (step-1)/3) {
            for (int i = step; i < array.length; i++) {
                for (int j = i; j > step - 1; j -= step) {
                    if (array[j-step] > array[j]) {
                        swapValue(array, j, j - step);
                    }
                }
            }
        }
    }

    private static int calculationStepLength(int length) {
        int res = 1;
        while (res < length / 3) {
            res = res * 3 + 1;
        }
        return res;
    }

    private static void swapValue(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

}

那么，本人来展示下运行结果：

---

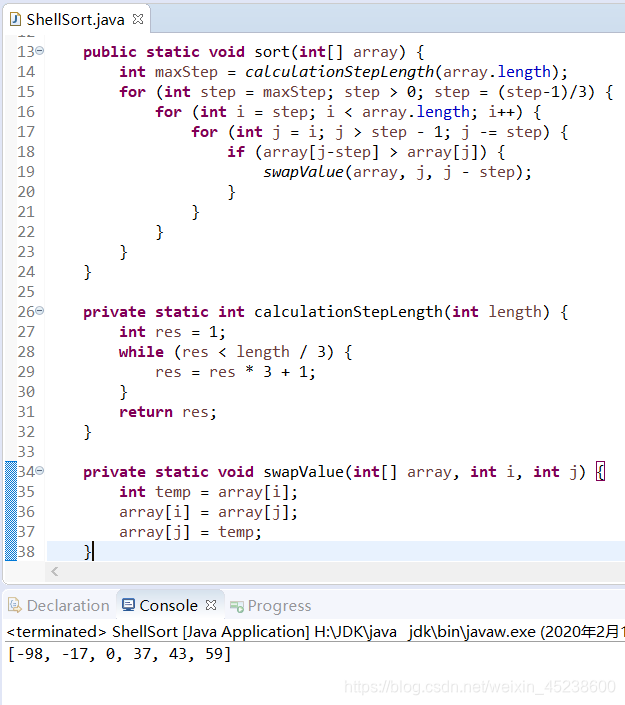
快速排序

时间复杂度：

O(nlog n)

基本原理：

首先选取数组中的第一个数作为基准数

然后将比它大的数放在它的左边，比它小的数放在右边

这样一来，这个基准数的位置就找好了

接下来，我们再对左右两个区间的数分别进行如上的操作

重复上面的所有操作，直到每个区间只有一个数为止

动态演示：

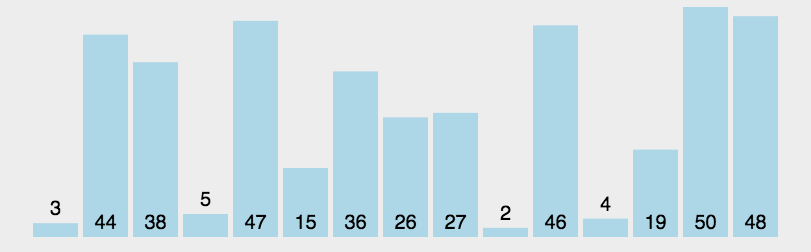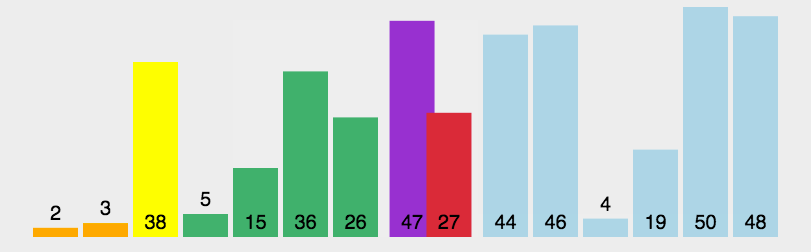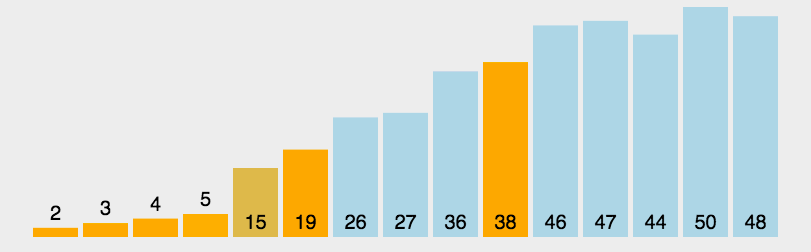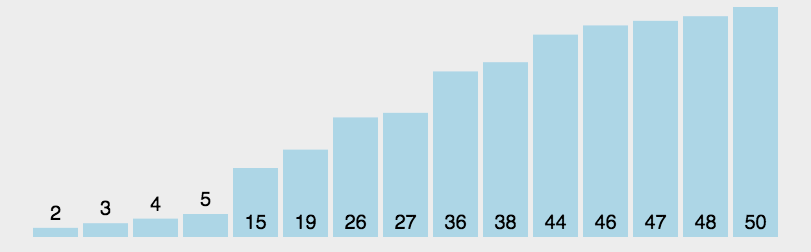
代码实现：

package aboutArraySort;

import java.util.Arrays;

public class QuickSort {

	public static void main(String[] args) {
        int[] array = {37, 59, 43, -98, -17, 0};
        sort(array);
        System.out.println(Arrays.toString(array));
    }

    public static void sort(int[] array) {
        qiuckSort(array, 0, array.length-1);
    }

    private static void qiuckSort(int[] array, int start, int end) {
        if (start < end) {
            int refIndex = getRefIndex(array, start, end);
            qiuckSort(array, start, refIndex-1);
            qiuckSort(array, refIndex+1, end);
        }
    }

    private static int getRefIndex(int[] array, int start, int end) {
        int i = start;
        int j = end;
        int temp = array[start];

        while (i < j) {
            while (i<j && (array[j]>=temp)) {
                j--;
            }
            if (i < j) {
                array[i] = array[j];
                i++;
            }

            while (i<j && (array[i]<temp)) {
                i++;
            }
            if (i < j) {
                array[j] = array[i];
                j--;
            }
        }
        array[i] = temp;
        return i;
    }

}

那么，本人来展示下运行结果：

---

归并排序

时间复杂度：

O(nlog n)

基本原理：

假设一个数组是由length个有序数组组成的

然后两两排序

之后再将每两个数组元素看作是一个有序序列，再重复上面的步骤

直到将整个数组看作是一个有序序列，那么这个数组就已经排好序了

动态演示：

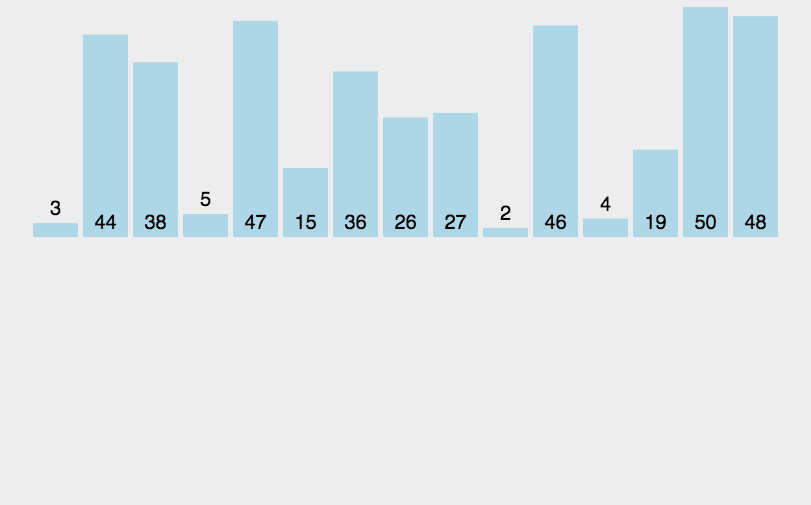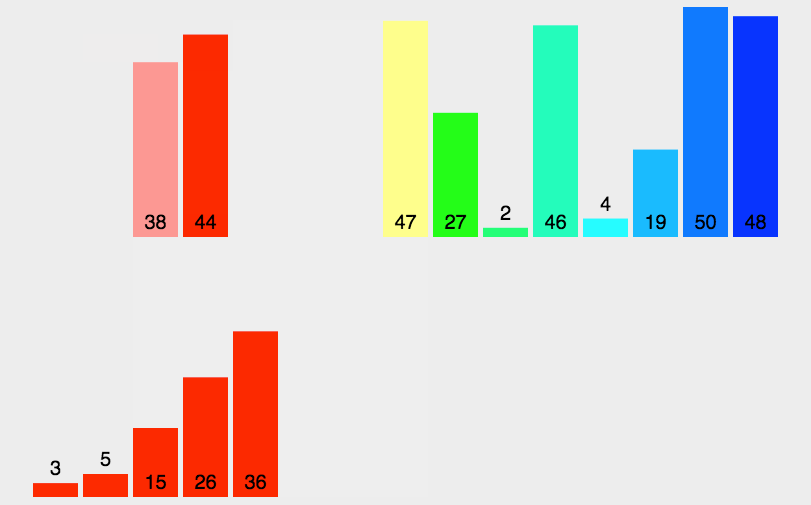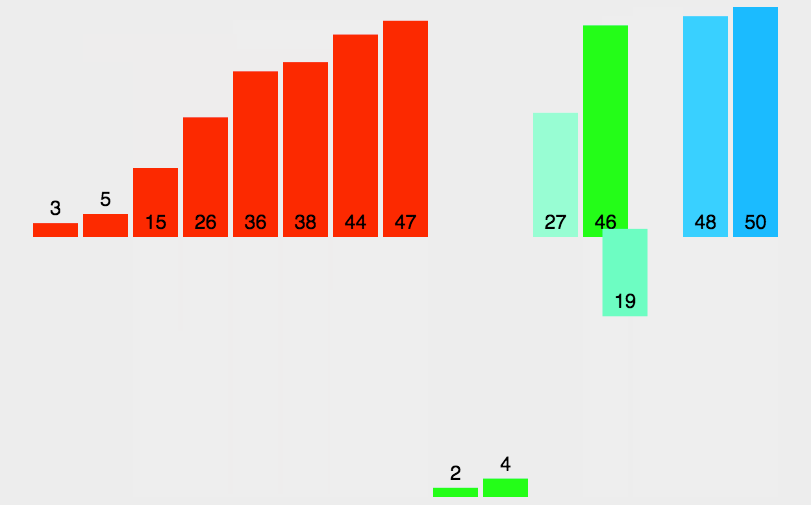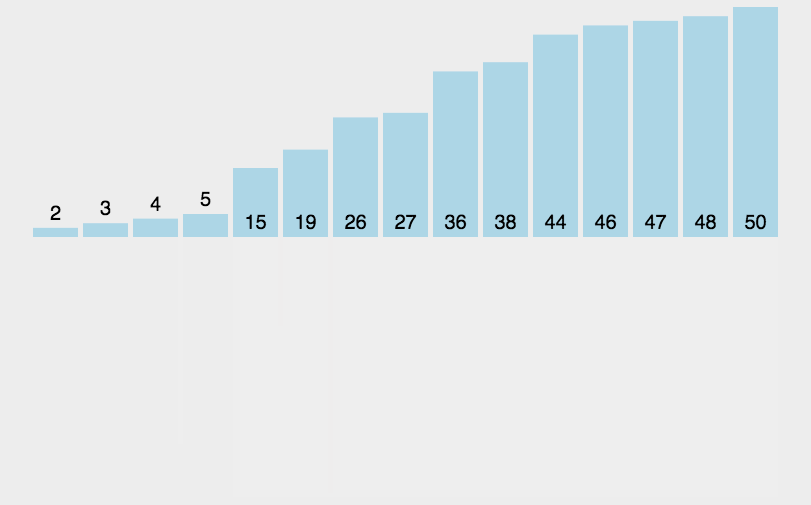
代码实现：

package aboutArraySort;

import java.util.Arrays;

public class MergeSort {

	public static void main(String[] args) {
        int[] array = {37, 59, 43, -98, -17, 0};
        sort(array);
        System.out.println(Arrays.toString(array));
    }

    public static void sort(int[] array) {
        mergeSort(array, 0, array.length - 1);
    }

    private static void mergeSort(int[] array, int startIndex, int endIndex) {
        int centerIndex = (endIndex + startIndex)/2;
        if (startIndex < endIndex) {
            mergeSort(array, startIndex, centerIndex);
            mergeSort(array, centerIndex + 1, endIndex);
            merge(array, startIndex ,endIndex);
        }
    }

    /* 合并两个子数组 */
    private static void merge(int[] array, int startIndex, int endIndex) {
        int centerIndex = (endIndex + startIndex)/2;
        int i = startIndex;
        int j = centerIndex + 1;
        int[] res = new int[endIndex - startIndex + 1];
        int index = 0;

        //向临时数组中存储元素
        while ((i <= centerIndex) && (j <= endIndex)) {
            if (array[i] <= array[j]) {
                res[index++] = array[i++];
            } else {
                res[index++] = array[j++];
            }
        }
        //处理剩余元素
        while (i <= centerIndex) {
            res[index++] = array[i++];
        }
        while (j <= endIndex) {
            res[index++] = array[j++];
        }
        //将临时数组中的值转交给原数组
        for (int k = 0; k < res.length; k++) {
            array[k + startIndex] = res[k];
        }
    }

}

那么，本人来展示下运行结果：

---

基数排序

时间复杂度：

O(d(r+n))

(d——长度

r —— 关键字基数

n ——关键字个数)

基本原理：

首先来建立编号为0~9的10个数组

然后将原数组中的每个元素通过个位的数值来存放在10个新数组对应的一个当中

然后再按照0~9的顺序将所有存入的数取出

再来按照原数组中的每个值的十位的值，来存放在10个新数组对应的一个当中

重复上面的操作，直到最高位也被这样比较了

等最后一次取出时，这个数组就排好序了

（由于我们设置的数组只能用于识别每一位的值，而不能识别正负，

所以，基数排序只能用于排列正数）

动态演示：

代码实现：

package aboutArraySort;

import java.util.Arrays;

public class RadixSort {

	public static void main(String[] args) {
        int[] array = {37, 59, 43, 0};
        sort(array);
        System.out.println(Arrays.toString(array));
    }

    public static void sort(int[] array) {
        int[][] tempArray = new int[10][array.length];
        int[] capacity = new int[10];
        int max = getMax(array);
        int maxLen = String.valueOf(max).length();

        for (int i = 0, n = 1; i < maxLen; i++, n *= 10) {
            for (int j = 0; j < array.length; j++) {
                //取每轮相应的位的值
                int remainder = array[j]/n%10;
                tempArray[remainder][capacity[remainder]++] = array[j];
            }
            //取出临时数组中的元素
            int index = 0;
            for (int k = 0; k < capacity.length; k++) {
                if (capacity[k] != 0) {
                    for (int x = 0; x < capacity[k]; x++) {
                        array[index++] = tempArray[k][x];
                    }
                    //清空临时数组中的记录，以便我们之后再次使用这个数组
                    capacity[k] = 0;
                }
            }
        }

    }

    private static int getMax(int[] array) {
        int res = array[0];

        if (array.length < 2) {
            return res;
        }
        for (int i = 1; i < array.length; i++) {
            if (array[i] > res) {
                res = array[i];
            }
        }
        return res;
    }

}

那么，本人来展示下运行结果：

---

堆排序

时间复杂度：

O(nlog n)

基本原理：

首先将待排序列构造成一个大根堆，所以，此时的根节点就是整个数组的最大值

然后将根所存储的数值和末尾元素进行交换，这样一来，末尾元素就是本数组的最大值

之后将除末尾元素外的剩余元素再次转换为大根堆，反复进行上述的操作

待剩余最后一个元素时，这个数组就排序完成了

动态演示：

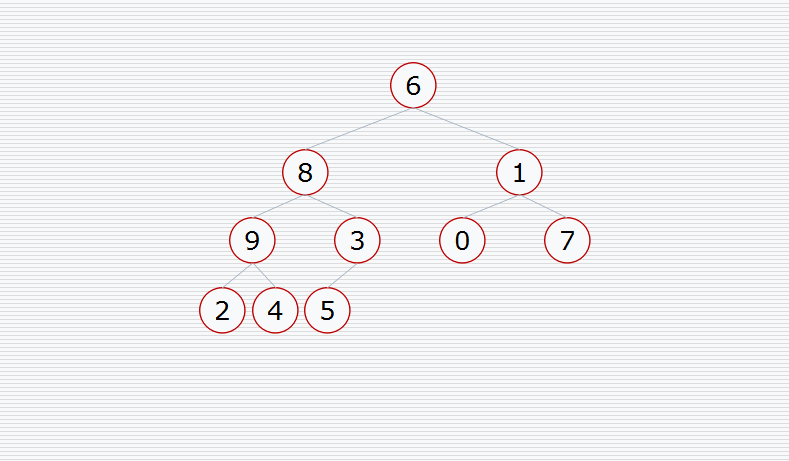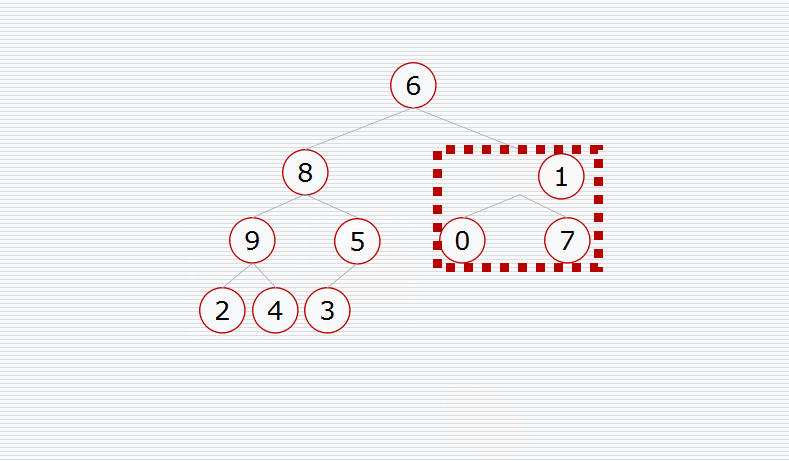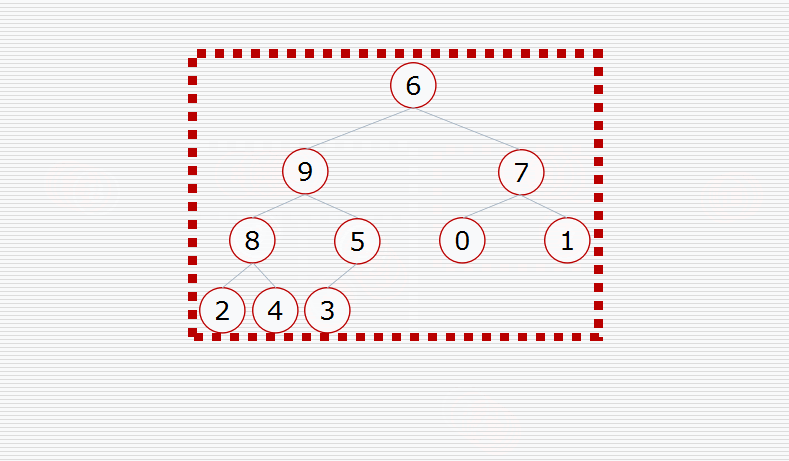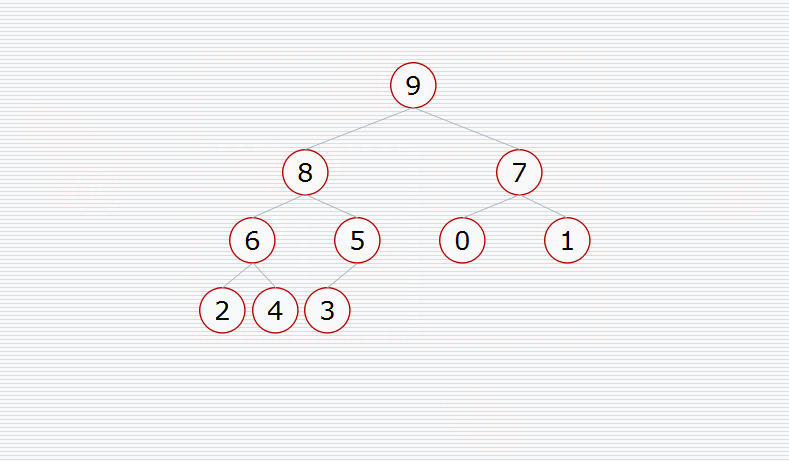
代码实现：

package aboutArraySort;

import java.util.Arrays;

public class HeapSort {

	public static void main(String[] args) {
        int[] array = {37, 59, 43, -98, -17, 0};
        sort(array);
        System.out.println(Arrays.toString(array));
    }

    public static void sort(int[] array) {
        for (int i = (array.length-1)/2; i >= 0; i--) {
            toBigRootHeap(array, array.length, i);
        }
        for (int i = array.length-1; i > 0; i--) {
            //进行调换
            swapValue(array, i, 0);
            //再将剩余元素调换成大顶堆
            toBigRootHeap(array, i, 0);
        }
    }

    private static void toBigRootHeap(int[] array, int size, int index) {
        //获取左右孩子的下标
        int leftChildIndex = index * 2 + 1;
        int rightChildIndex = index * 2 + 2;
        //获得此根与左右孩子中的最大值的下标
        int maxIndex = index;
        if ((leftChildIndex < size) && (array[leftChildIndex] > array[maxIndex])) {
            maxIndex = leftChildIndex;
        }
        if ((rightChildIndex < size) && (array[rightChildIndex] > array[maxIndex])) {
            maxIndex = rightChildIndex;
        }
        //交换这三个数值的位置，将此节点转换为“大根”
        if (maxIndex != index) {
            swapValue(array, index, maxIndex);
            //排序底下的节点，防止调换完导致底下的节点无法形成大根堆
            toBigRootHeap(array, size, maxIndex);
        }

    }

    private static void swapValue(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

}

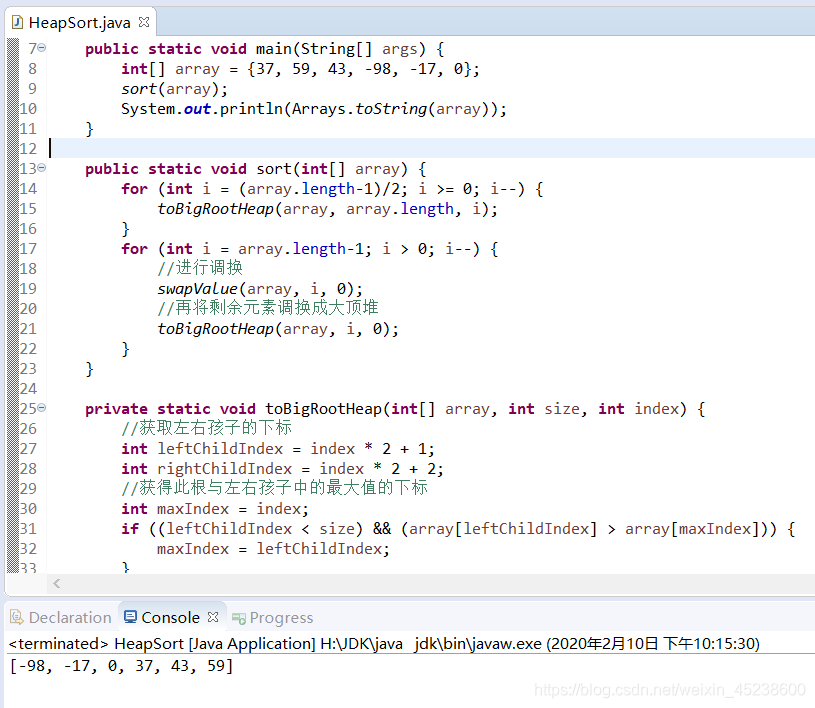
那么，本人来展示下运行结果：

---