FPGA实现CRC编码

首先CRC应用的主要场景：

在数据通信中要求数据的高度可靠性，但实际上由于信道不理想或者噪声干扰都会导致数据的误码率

那么对于信道不理想产生的影响可以用均衡的方法进行改善或者消除，而噪声干扰的数据误码通过差错控制消除，而差错控制的核心是差错编码，其中CRC由于编码和解码简单，检错和纠错能力强得到广泛应用。对随机错误和突发错误都能以较低冗余度进行严格检验

其特征是信息段和校验字段的长度可以任意选定。

在数据存储和数据通信领域，CRC无处不在：著名的通信协议X.25的FCS（帧检错序列）采用的是CRC/CCITT，ARJ/LHA等压缩工具软件采用的是CRC32，磁盘驱动器读写采用的日式CRC16，通常用到的图像存储格式GIF/TIFF等也是采用CRC作为检错手段的

传输差错分为两种：1、比特差错（1可能变成0，0可能变成1）；2、收到的帧没有出现差错，但出现了帧丢失、帧重复等。故在数据链路层使用CRC校验，能够实现无比特差错的传输，但这还不是可靠传输。 数据的可靠传输用哪个到了TCP协议，（

可靠数据传输的原理

）

 

2.CRC校验的基本原理：

　　CRC码是由两部分组成的，前部分是信息码，就是需要校验的信息，后部分是校验码，如果CRC码长共n bit，信息码长k bit，就称为(n,k)码，剩余的r bit即为校验位。如：(7,3)码：110 1001，前三位110为信息码，1001为校验码。

3.校验码的生成规则：

　　1)将原信息码左移r bit，右侧补零，如 110--> 110 0000；

　　2)用110 0000除以g(x)  (注意，使用的是模2除法,见下文)，得到的余数即为CRC校验码；

　　3)将校验码续接到信息码的尾部，形成CRC码。

4.关于生成多项式g(x)

　　在产生CRC校验码时，要用到除法运算，一般来说，这是比较麻烦的，因此，把二进制信息预先转换成一定的格式，这就是CRC的多项式表示。二进制数表示为生成多项式的系数，如下：

　　

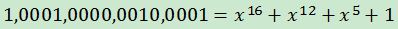
　　所有二进制数均被表示为一个多项式，x仅是码元位置的标记，因此我们并不关心x的取值，称之为码多项式。(我没研究过CRC代数推理过程，没体会到用多项式计算的方便之处，这里要学会的就是给出生成多项式g(x)，能写出对应的二进制即可)

　　常见的生成多项式如下： CRC-12码通常用来传送6-bit字符串。CRC-16及CRC-CCITT码则用来传送8-bit字符，其中CRC-16为美国采用，而CRC-CCITT为欧洲国家所采用。CRC-32码用途有限。校验码的位数越多，差错检测能力越高

　　

实现的过程已经明确，那么对多项式做模2除法如何实现呢？这里就需要涉及到一种叫LFSR（线性反馈移位寄存器）的使用http://www.cnblogs.com/BitArt/archive/2012/12/22/2827005.html讲的很详细，是一种伪随机数产生的方式，

有所改进的地方就是，可以将伪随机数发生器看作一个Moore型状态机，它的输出只与当前的状态有关；而此时利用LFSR电路，需要引入数据输入端，输出不仅取决于当前的状态，还取决于输入信号，相当于Mealy型状态机，如下图：

　　

注意对比与伪随机数产生器中该反馈支路的区别！

　　反馈项g_r+1g_r……g₀为生成多项式的系数，依然是1代表存在反馈，0代表不存在反馈；此电路可以完成上述的模2除法操作，若我们要求0xaa的CRC校验码，则从高位到低位顺序输入0xaa共8 bit后，D15……D0中的数据即为所要求的余数，即CRC校验位。

附上代码：实现的是一个有4位信息码，5位校验码的数据编码

module CRC5_GEN(
input rst,
input clk,
input [3:0] data_in,
input d_valid,
output reg[4:0] crc
);

integer i;
reg feedback;
reg [4:0] crc_tmp;
always @(posedge clk or negedge rst)
begin
if(!rst)
crc <= 5'b0;
else if(d_valid==1'b0)
crc <= 5'b0;
else
crc <= crc_tmp;
end

always@( data_in or crc)
begin
crc_tmp = crc;
for(i=3; i>=0; i=i-1)
begin
feedback = crc_tmp[4] ^ data_in[i];
crc_tmp[4] = crc_tmp[3];
crc_tmp[3] = crc_tmp[2];
crc_tmp[2] = crc_tmp[1] ^ feedback;
crc_tmp[1] = crc_tmp[0];
crc_tmp[0] = feedback;
end

end

endmodule

Verilog 实现http://www.cnblogs.com/BitArt/archive/2012/12/26/2833100.html

​      由上面的分析大家应该可以写出串行的code。但是并行的怎么写，以及具体的原理可以参考。

写过之后的验证可以使用参考这个网址。​好了，就写这些了。