题解 P4344 【[SHOI2015]脑洞治疗仪】

前言

这道题目呢，看上去很难，实际上我们可以用线段树解决这道题目。

正文

我们维护 sum、len、tag、lmax、rmax、ans。

sum 就是这段区间非脑洞的个数

len 就是这段区间的长度

tag 就是我们的 lazy_tag

lmax 就是从左开始的连续脑洞个数

rmax 就是从右开始的连续脑洞个数

ans 就是这段区间最大的连续脑洞

建树

由于 len 是不变的，所以我们可以建树的时候就求出 len

t[num].len=r-l+1;

pushup

sum

sum 就是左子树和右子树的 sum 的和。

t[num].sum=t[ls].sum+t[rs].sum;

lmax

lmax 的话有两种情况

第 \(1\) 种情况

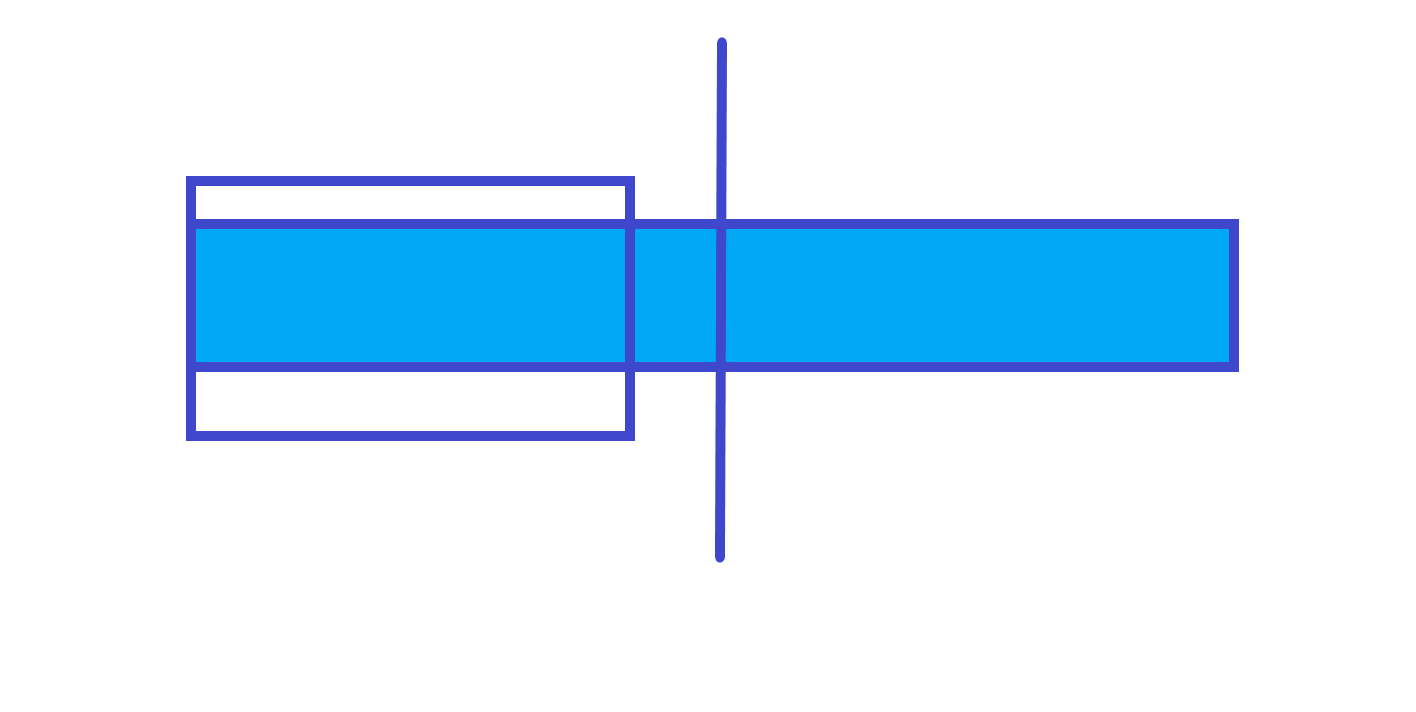
lmax=左子树的 lmax

第 \(2\) 中情况

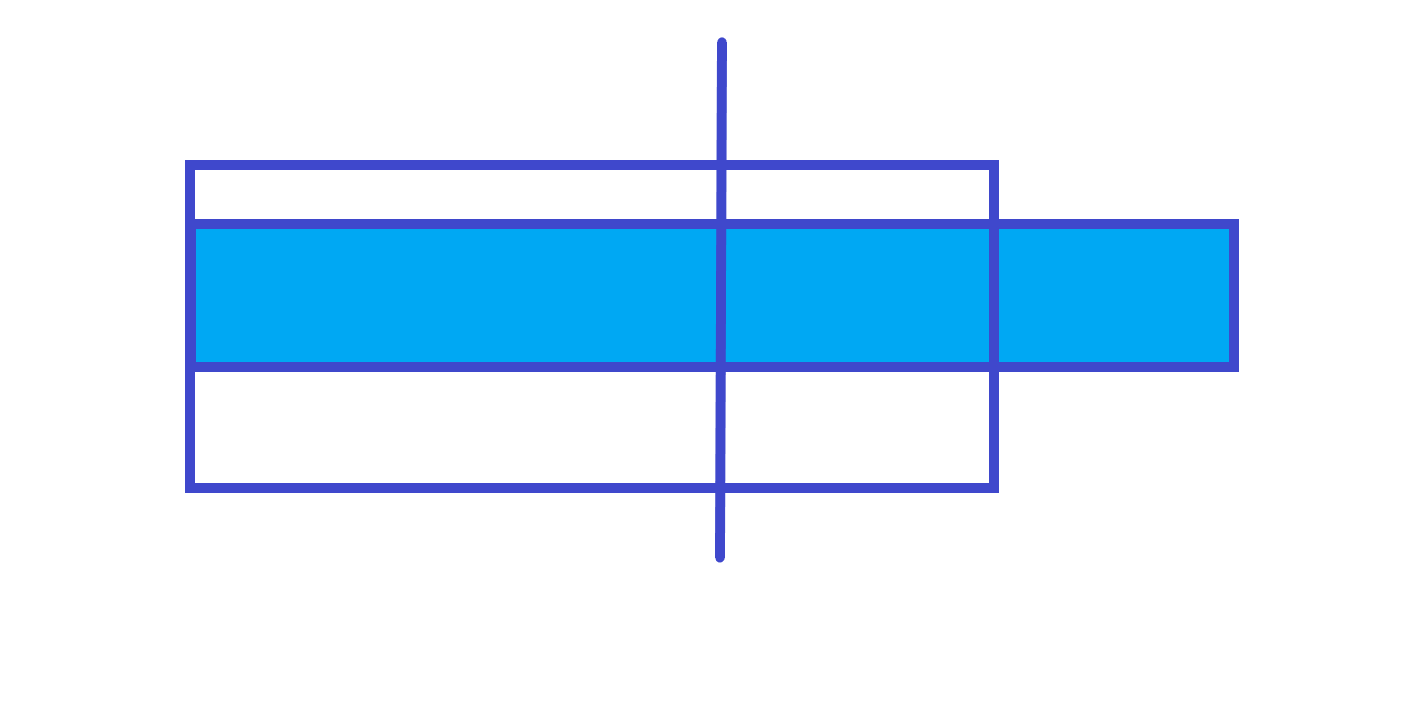
lmax=左子树的 len + 右子树的 lmax

if(t[ls].lmax==t[ls].len)t[num].lmax=t[ls].len+t[rs].lmax;
else t[num].lmax=t[ls].lmax;

rmax

rmax 的话也两种情况

第 \(1\) 种情况

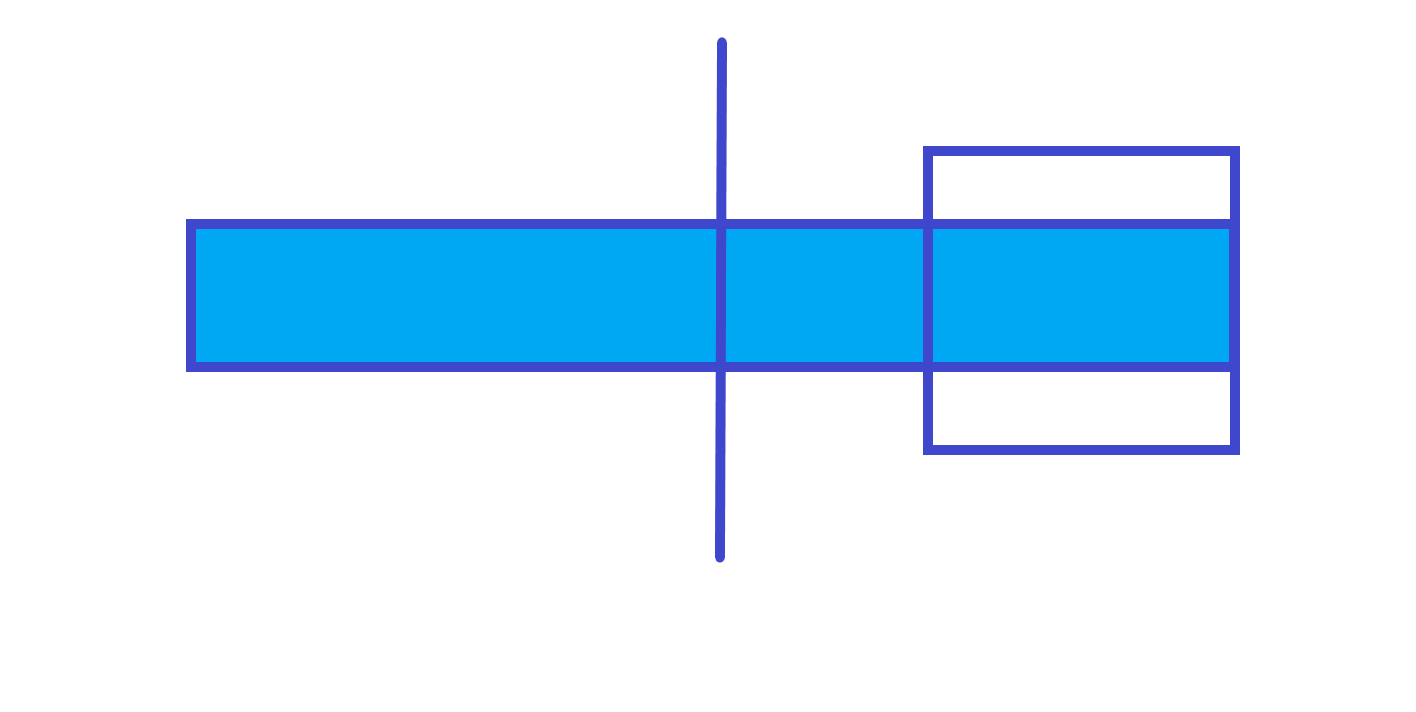
rmax=右子树的 rmax

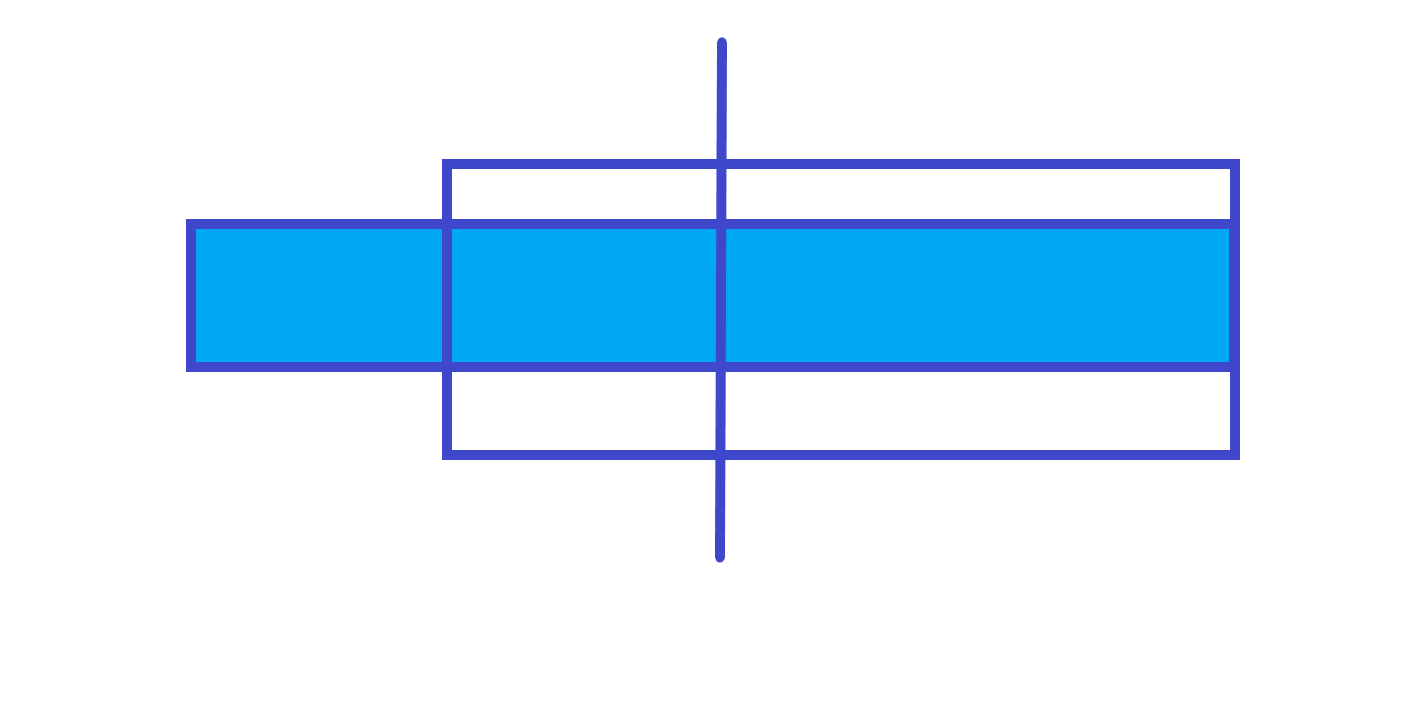
lmax=右子树的 len + 左子树的 rmax

if(t[rs].rmax==t[rs].len)t[num].rmax=t[rs].len+t[ls].rmax;
else t[num].rmax=t[rs].rmax;

ans

ans 的话有 \(3\) 种情况

第 \(1\) 种情况

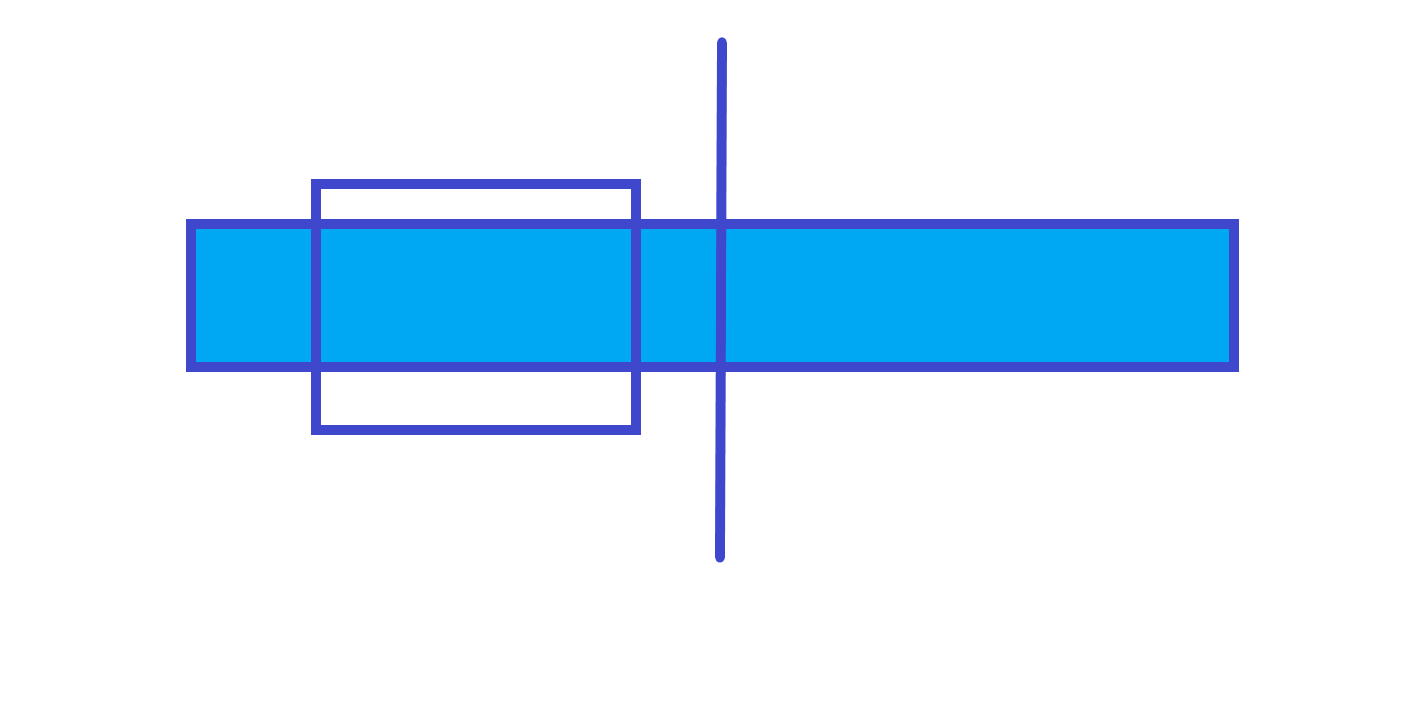
ans=左子树的 ans

第 \(2\) 种情况

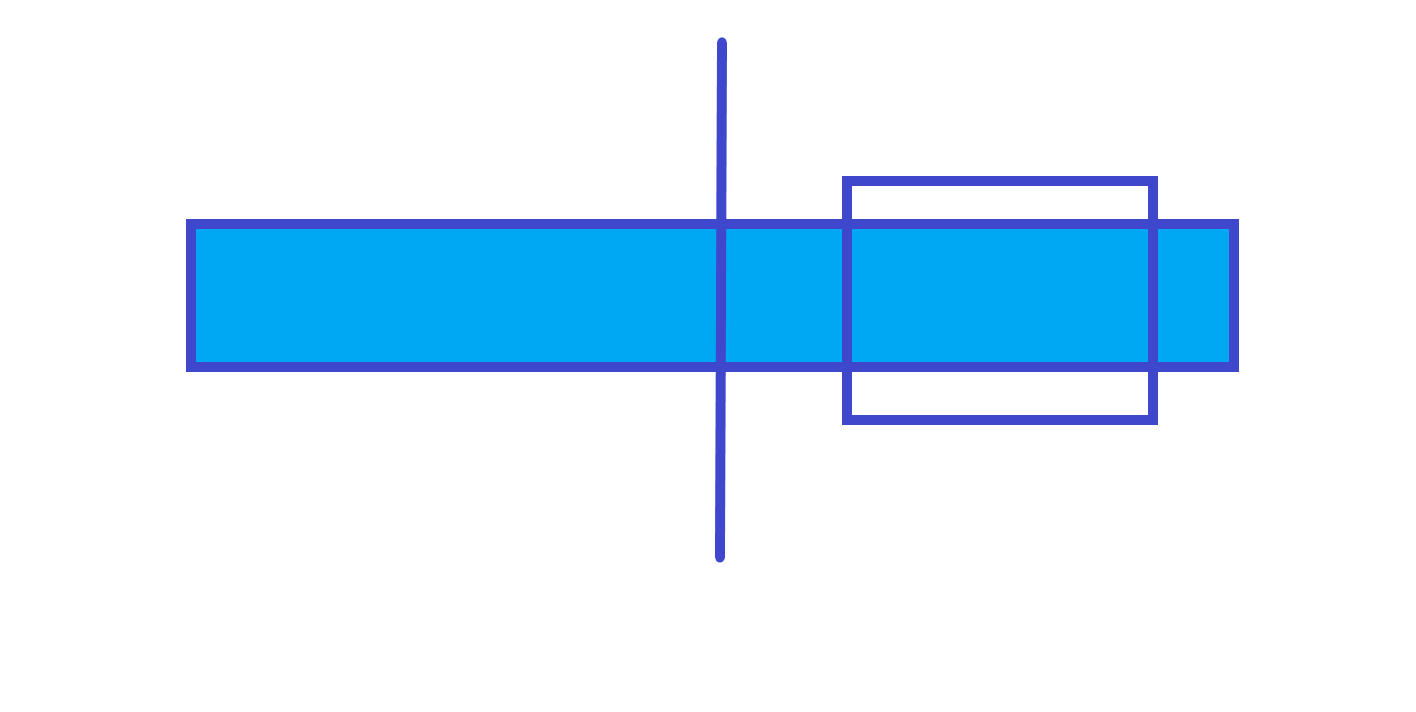
ans=右子树的 ans

第 \(3\) 种情况

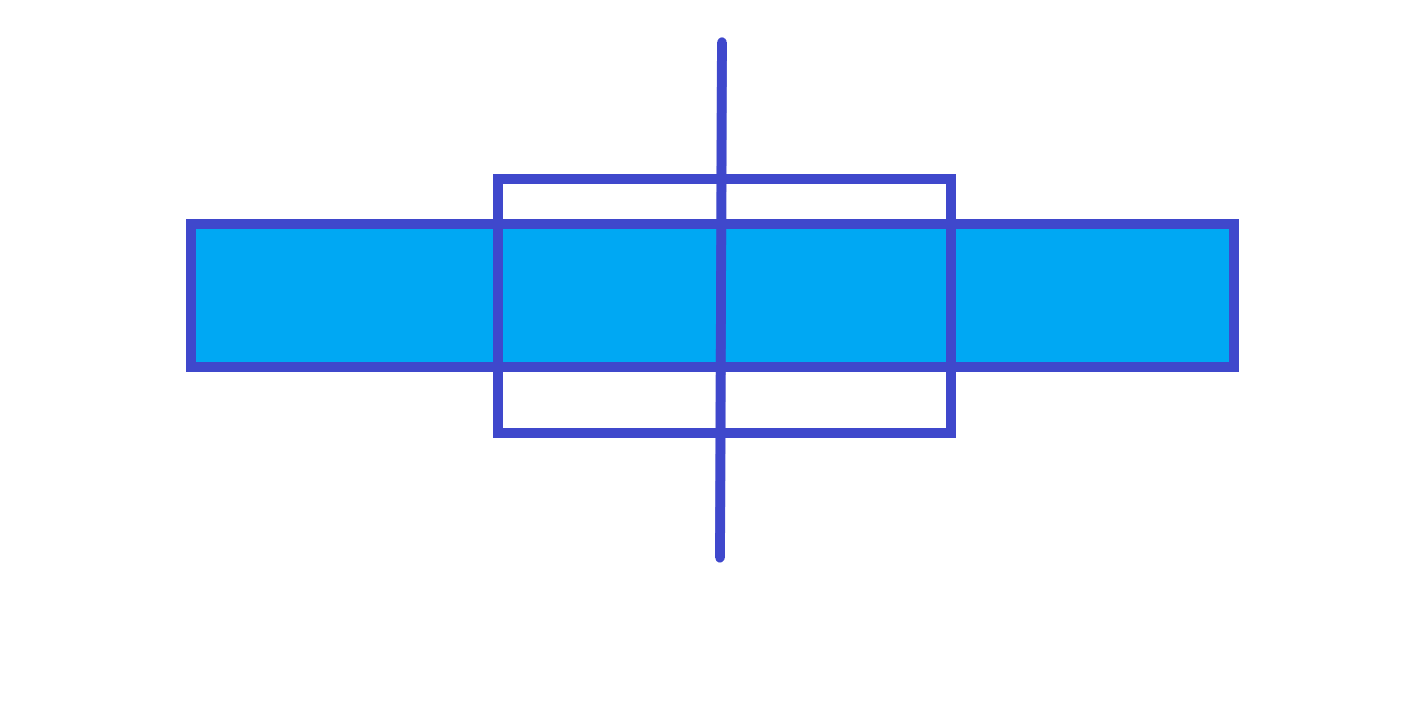
ans=左子树的 rmax+右子树的 lmax

t[num].ans=max(max(t[ls].ans,t[rs].ans),t[ls].rmax+t[rs].lmax);

pushdown

tag

我们的 tag 有 3 种值，分别为 0，1，2

0 表示什么都没有

1 表示全部为脑洞

2 表示全部不为脑洞

0

0 的话，代表没有任何操作，不要管。

1

我们对照上面的发现：

ans、lmax、rmax 都为 len。

而 sum 则为 0。

tag 的标记当然要打啦。

void down1(int num){
	t[num].ans=t[num].lmax=t[num].rmax=t[num].len;
	t[num].sum=0;
	t[num].tag=1;
}

2

我们对照上面的发现：

ans、lmax、rmax 都为 0。

而 sum 则为 len。

tag 的标记当然要打啦。

void down2(int num){
	t[num].ans=t[num].lmax=t[num].rmax=0;
	t[num].sum=t[num].len;
	t[num].tag=2;
}

二分

我们可以发现，操作 2 就是先统计一遍 \([l0,r0]\) 中非脑洞的个数。

然后把 \([l0,r0]\) 这段区间全部变成脑洞，再去在 \([l1,r1]\) 这段区间里找到从 \(l0\) 开始算起最右边脑洞个数 \(\leq[l0,r0]\) 中脑洞的个数。

我们发现脑洞个数是单调递增的，所以我们可以二分。

我采用的写法是左闭右开。

void work(){
	int x=query0(1,l0,r0);//统计
	if(x==0)return;//这里要注意，否则我们的边界就是错的
	change(1,l0,r0,1);//全部变成脑洞
	int l=l1,r=r1+1;//二分的边界
	while(l+1<r){//经典写法
		int mid=(l+r)>>1;//求mid
		if(query1(1,l1,mid)<=x)l=mid;//小于等于
		else r=mid;
	}
	change(1,l1,l,2);//填上去
}

代码

复杂度 \(O(n \log n + q \log^2 n)\)

#include <bits/stdcpp.h>
#define ls num<<1
#define rs num<<1|1
using namespace std;
typedef long long ll;
template<typename T>inline void read(T &FF){
	T RR=1;FF=0;char CH=getchar();
	for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
	for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
	FF*=RR;
}
template<typename T>inline void write(T x){
	if(x<0)putchar('-'),x*=-1;
	if(x>9)write(x/10);
	putchar(x%10+48);
}
template<typename T>inline void writen(T x){
	write(x);
	puts("");
}
const int N=2e5+10;
struct Tree{
	int l,r,lmax,rmax,sum,tag,len,ans;
}t[N<<2];
int n,m,l0,r0,l1,r1,f;
void pushup(int num){
	t[num].sum=t[ls].sum+t[rs].sum;
	if(t[ls].lmax==t[ls].len)t[num].lmax=t[ls].len+t[rs].lmax;
	else t[num].lmax=t[ls].lmax;
	if(t[rs].rmax==t[rs].len)t[num].rmax=t[rs].len+t[ls].rmax;
	else t[num].rmax=t[rs].rmax;
	t[num].ans=max(max(t[ls].ans,t[rs].ans),t[ls].rmax+t[rs].lmax);
}
void down1(int num){
	t[num].ans=t[num].lmax=t[num].rmax=t[num].len;
	t[num].sum=0;
	t[num].tag=1;
}
void down2(int num){
	t[num].ans=t[num].lmax=t[num].rmax=0;
	t[num].sum=t[num].len;
	t[num].tag=2;
}
void pushdown(int num){
	if(t[num].tag==1){
		down1(ls);down1(rs);
		t[num].tag=0;
	}
	if(t[num].tag==2){
		down2(ls);down2(rs);
		t[num].tag=0;
	}
}
void build(int num,int l,int r){
	t[num].tag=0;
	t[num].l=l;
	t[num].r=r;
	t[num].len=r-l+1;
	if(l==r){
		t[num].sum=1;
		t[num].ans=t[num].lmax=t[num].rmax=0;
		return;
	}
	int mid=(l+r)>>1;
	build(ls,l,mid);
	build(rs,mid+1,r);
	pushup(num);
}
void change(int num,int x,int y,int z){
	if(t[num].l>=x&&t[num].r<=y){
		if(z==1)down1(num);
		if(z==2)down2(num);
		return;
	}
	pushdown(num);
	if(t[ls].r>=x)change(ls,x,y,z);
	if(t[rs].l<=y)change(rs,x,y,z);
	pushup(num);
}
int query0(int num,int x,int y){
	if(t[num].l>=x&&t[num].r<=y)return t[num].sum;
	pushdown(num);
	if(t[ls].r<x)return query0(rs,x,y);
	if(t[rs].l>y)return query0(ls,x,y);
	return query0(ls,x,y)+query0(rs,x,y);
}
int query1(int num,int x,int y){
	if(t[num].l>=x&&t[num].r<=y)return t[num].len-t[num].sum;
	pushdown(num);
	if(t[ls].r<x)return query1(rs,x,y);
	if(t[rs].l>y)return query1(ls,x,y);
	return query1(ls,x,y)+query1(rs,x,y);
}
void work(){
	read(l1);read(r1);
	int x=query0(1,l0,r0);
	if(x==0)return;
	change(1,l0,r0,1);
	int l=l1,r=r1+1;
	while(l+1<r){
		int mid=(l+r)>>1;
		if(query1(1,l1,mid)<=x)l=mid;
		else r=mid;
	}
	change(1,l1,l,2);
}
int query2(int num,int x,int y){
	if(t[num].l>=x&&t[num].r<=y)return t[num].ans;
	pushdown(num);
	if(t[ls].r<x)return query2(rs,x,y);
	if(t[rs].l>y)return query2(ls,x,y);
	return max(max(query2(ls,x,y),query2(rs,x,y)),min(t[ls].rmax,t[rs].l-x)+min(t[rs].lmax,y-t[ls].r));
}
int main(){
	read(n);read(m);
	build(1,1,n);
	while(m--){
		read(f);read(l0);read(r0);
		switch(f){
			case 0:change(1,l0,r0,1);break;
			case 1:work();break;
			case 2:writen(query2(1,l0,r0));break;
		}
	}
	return 0;
}

拓展

这道题目还有更优秀的解法，复杂度可以少掉一个 \(\log\) 也就是变成 \(O(n \log n+q \log{n})\)。

我们还是先统计非脑洞个数。

我们写一个函数 \(fill\) 就是我们用来把脑细胞填入脑洞的函数。我们要填 \(x\) 个脑细胞，会发现有 \(2\) 种情况。

• 第 \(1\) 种情况是所有脑细胞都填入左子树。

• 第 \(2\) 种情况是所有脑细胞不仅把左边填满，还有多的放到右子树。

我们可以根据这个写代码：

int fill(int num,int l,int r,int x){//fill的返回值就是剩余的脑细胞数量
	if(x==0)return 0;
	if(t[num].l>=l&&t[num].r<=r&&t[num].sum<=x){
		int s=t[num].sum;//务必要先存起来
		down2(num);
		return x-s;
	}
	pushdown(num);int ans;
	if(t[ls].r<l)ans=fill(rs,l,r,x);
	else if(t[rs].l>r)ans=fill(ls,l,r,x);
		else ans=fill(rs,l,r,fill(ls,l,r,x));
	pushup(num);
	return ans;//答案
}