ACM博弈论基础

博弈论的题目有如下特点：

有两名选手
两名选手交替操作，每次一步，每步都在有限的合法集合中选取一种进行
在任何情况下，合法操作只取决于情况本身，与选手无关
游戏败北的条件为：当某位选手需要进行操作时，当前没有任何可以执行的合法操作

下面介绍几个经典的博弈。

巴什博弈（Bash Game）

一堆n个物品，两个人轮流从中取出1~m个，最后取光者胜（不能继续取的人输）。

同余定理：$n=k*(m+1)+r$，先者拿走$r$个，那么后者无论拿走$1~m$个先者只要的数目使和为$m+1$，那么先手必赢。反之若$n=k*(m+1)$，那么先手无论怎样都会输。

if (n % (m + ))  return false;

else  return true;

威佐夫博弈（Wythoff Game）

有两堆各若干物品，两个人轮流从任意一堆中至少取出一个或者从两堆中取出同样多的物品，规定每次至少取一个，至多不限，最后取光者胜。

这里的必输局势：（0，0）、（1，2）、（3，5）、（4，7）、（6，10）、（8，13）、（9，15）、（11，18）、（12，20）。从这些必输局势可以发现，每组的第一个是前面没有出现的最小正整数，$a_k = [k * (1+\sqrt{5}) / 2],\ b_k = a_k + k,\ k = 0,1,2,3...$。

所以，先求出差值，差值*黄金分割比 == 最小值的话后手赢，否者先手赢。

double r = (sqrt() + ) / ;

int d = abs(a - b) * r;

if (d != min(a, b))  return true;

else  false;

注：如果a,b的值非常大的话，需要高精度来计算这个double类型的r。

斐波那契博弈（Fibonacci Nim Game）

一堆石子有n个，两人轮流取，先取者第一次可以去任意多个，但是不能取完，以后每次取的石子数不能超过上次取子数的2倍。取完者胜。

同样是一个规律：先手胜当且仅当n不是斐波那契数。

f[] = f[] = ;

for (int i = ; f[i - ] < n; i++)

{

    f[i] = f[i - ] + f[i - ];

    if (f[i] == n)  return true;

}

return false;

尼姆博弈（Nimm Game）

有n堆物品，两人轮流取，每次取某堆中不少于1个，最后取完者胜。

假如有3堆物品(a,b,c)
（0，0，0）状态时先手是一个必输局势因为没有东西可取，(0,n,n) 状态时也是必输局势只要后者在另一堆取得物品与前者一样多时那么前者也就是必输局势。慢分析(1,2,3)也是一个必输局势。如果我们将其转化为二进制形式并通过异或运算(^)我们会发现：
0001^0010^0011=0000
通过验证所有的堆数量累^后只要为0就都是必输局势，所以我们就只要记住这个规则：将n堆物品数量全部异或后结果为0先手必败，否则必胜。

int res = ;

for (int i = ; i <= n; i++)

    res ^= arr[i];

if (res)  return true;

else  return false;

但是，实际问题中不可能给出如此标准的博弈模型，对于更加一般的博弈问题，我们该如何求解呢？通过SG函数转换为尼姆博弈。

SG函数

首先给出一种ICG博弈游戏模型，给定一个有向无环图和一个起始顶点上的一枚棋子，两名选手交替的将这枚棋子沿着有向边进行移动，无法移动者判负。

将ICG问题进行转化：任何一个ICG都可以通过把每个局面看作一个顶点，对每个局面和它的子局面连一条有向边来抽象这个“有向图游戏”。

于是我们将ICG问题转化为上述这个游戏，再通过寻找这个游戏的一般解法来处理ICG问题。

首先定义mex(minimal excludant)运算，这是定义于一个集合的运算，表示最小的不属于这个集合的最小非负整数。例如mex{0,1,2,4}=3，mex{2,3,4}=0，mex{}=0.

SG函数（Sprague-Grundy）：对于一个给定的有向无环图，定义关于这个图的每个顶点的SG函数如下：$sg(x) = mex\{sg(y) \ | \ y是x的后继 \}$

SG函数的求法：

找出必败态
找出当前所有状态的前驱结点
根据定义计算结点SG值
重复上述步骤，直到整棵树建立完成

按上述步骤建成的树如下：

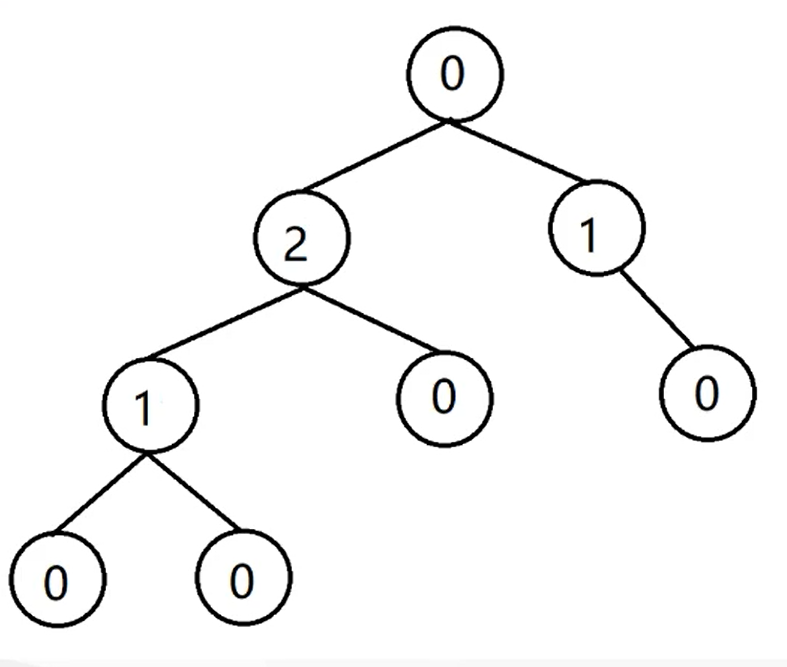
这颗树有什么意义呢？比如说我们将一个顶点放在根节点上，当前这个点的sg值为0，说明当前这个点是必败态。为什么这么说呢？我们将这个点交替进行移动，先手有两种选择，往右移动，显然后手再移动一步就进入必败态；往左移动，后手会选择往右移动，先手同样进入必败态。

如何通过SG函数值来解决之前的有向图问题呢？对于n个棋子，设它们对应的顶点的SG函数值分别为$\{a_1,a_2,...a_n\}$，再设局面$\{a_1,a_2,...a_n\}$时的Nim游戏的必胜策略是把$a_i$变成$k$，那么原游戏的一种必胜策略就是把第$i$枚棋子移动到一个SG值为$k$的顶点。

简单来说，我们让每个结点都拥有一个SG值（假设这个值为$x$），那么对于任何一个玩家操作（移动到当前结点的某个后继结点）实际上就是把棋子移动到0~x-1的某个结点上，等价的就是从x个物品中取走一个，最多x个！。

不是是觉得有点不对，单根据mex的定义，可能出现如下情况，移动到比自身SG值大的结点：

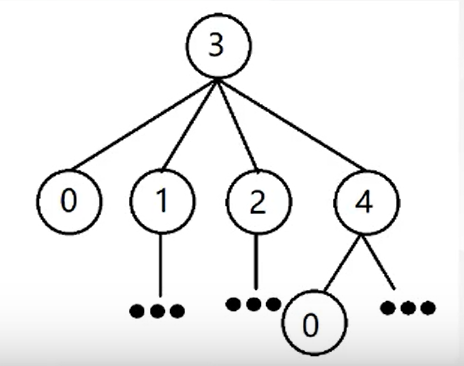
其实这种情况是不存在的，博弈问题中先手不会移动到对自己不利的局面的，在这里也就是不会移动到SG值为4的结点。

SG定理：所以我们可以定义有向图游戏的和。设$G_1,G_2,...G_n$为n个“有向图”游戏的和(Sum)，游戏G的移动规则是：任选一个子游戏$G_i$并移动上面的棋子。SG定理就是：$sg(G)=sg(G_1) \wedge sg(G_2) \wedge .... \wedge sg(G_n)$。也就是说，游戏的SG函数值就是它的所有子游戏的SG函数值的异或。

因此，当我们面对n个不同游组成的游戏时，只需要求出每个游戏的SG函数值，把这些SG值都看作Nim的石子堆，然后依照找Nim游戏的必胜策略的方法来找这个游戏的必胜策略。

参考链接：【算法讲堂】【电子科技大学】【ACM】博弈论基础