[luogu3768] 简单的数学题 [杜教筛]

题面：

传送门

实际上就是求：

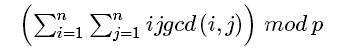
思路：

看到gcd就先反演一下，过程大概是这样：

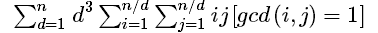
明显的一步反演

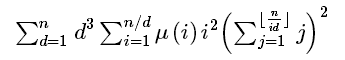
这里设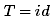，S(x)等于1到x的和

然后把枚举d再枚举T变成先枚举T再枚举其约数d，变形：

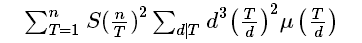
后面其中两项展开，把T提出来

S那里可以数论分块，那么只要S后面那个东西可以筛出来，就可以O(sqrt(n))

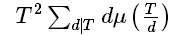
发现后面的那部分可以狄利克雷卷积一波

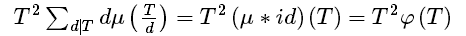
这明显是一个积性函数，但是n有10^10，所以不能线筛

考虑使用杜教筛，令上述函数为f，函数S为f的前缀和

套用杜教筛模板式

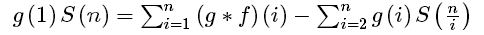
现在问题就是选一个合适的g函数了

我们知道欧拉函数有一个卷积性质：

那么我们令g(x)=x^2

此时g与f的卷积变成了：

看起来真是赏心悦目

于是杜教筛的递推式变成了这样的：

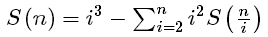
一波记忆化搜索带走AC

Code：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#define ll long long
using namespace std;
inline ll read(){
    ll re=,flag=;char ch=getchar();
    while(ch>''||ch<''){
        if(ch=='-') flag=-;
        ch=getchar();
    }
    while(ch>=''&&ch<='') re=(re<<)+(re<<)+ch-'',ch=getchar();
    return re*flag;
}
ll n,MOD,inv2,inv6;
ll phi[],pri[],tot=;bool vis[];
void init(){
    ll i,j,k;phi[]=;phi[]=;
    for(i=;i<=;i++){
        if(!vis[i]){
            pri[++tot]=i;phi[i]=i-;
        }
        for(j=;j<=tot;j++){
            k=i*pri[j];if(k>) break;
            vis[k]=;
            if(i%pri[j]==){
                phi[k]=1ll*phi[i]*pri[j]%MOD;
                break;
            }
            phi[k]=1ll*phi[i]*phi[pri[j]]%MOD;
        }
    }
    for(i=;i<=;i++) phi[i]=(phi[i-]+1ll*i*i%MOD*phi[i]%MOD)%MOD;
}
ll sum1(ll x){x%=MOD;return x*(x+)%MOD*inv2%MOD;}
ll sum2(ll x){x%=MOD;return x*(x+)%MOD*((x<<)+)%MOD*inv6%MOD;}
map<ll,ll>m;
ll S(ll x){
    if(x<=) return phi[x];
    if(m[x]) return m[x];
    ll re=sum1(x),tmp;re=re*re%MOD;ll i,j;
    for(i=;i<=x;i=j+){
        j=x/(x/i);
        tmp=sum2(j)-sum2(i-);tmp=(tmp+MOD)%MOD;
        re-=S(x/i)*tmp%MOD;re%=MOD;
    }
    return m[x]=(re+MOD)%MOD;
}
ll fpow(ll a,ll b){
    ll re=;a%=MOD;
    while(b){
        if(b&) re=a*re%MOD;
        b>>=;a=a*a%MOD;
    }
    return re;
}
int main(){
    MOD=read();n=read();ll i,j;ll ans=,tmp,tt;
    inv2=fpow(,MOD-);inv6=fpow(,MOD-);init();
    for(i=;i<=n;i=j+){
        j=n/(n/i);
        tmp=sum1(n/i);
        tmp=(tmp+MOD)%MOD;tmp=(tmp*tmp)%MOD;
        tt=S(j)-S(i-);
        tt=(tt+MOD)%MOD;
        ans=(ans+tmp*tt%MOD)%MOD;
    }
    printf("%lld\n",(ans+MOD)%MOD);
}