funk_SVD 个人理解

目标函数：

$ J = \frac{1}{2} \left\| R - PQ \right\|^{2} + \lambda \left( \left\|P \right\|^{2} +\left\| Q \right\|^{2} \right) $

矩阵R为$ m \times n$的稀疏矩阵(sparse matrix),考虑用 $ P_{m  \times r}$ 和 $  Q_ {r \times n }$ 两个矩阵的乘积  $ \hat{R} $ 去逼近矩阵R，误差用SSE，后面面 两项为 正则项。

1，Gradient Descent

$ J = \frac{1}{2}\sum _{\left(i,j \right) \in D} \left( r_{ij} - \sum_{k=1}^{r} p_{ik} q_{kj}\right)^2 + \lambda \left ( \left \| P \right \| ^2+ \left \| Q \right \|^2 \right )$

整体误差$ J $对 因子矩 P 中某元素 $ p_{ik} $ 的偏导数:

$\frac{\partial J}{\partial p_{ik}} = \sum _{\left(i,j \right) \in D} \left( r_{ij} - \sum_{k=1}^{r} p_{ik} q_{kj}\right)q_{kj}+ \lambda  p_{ik} $

偏导数矩阵应注意的几项：

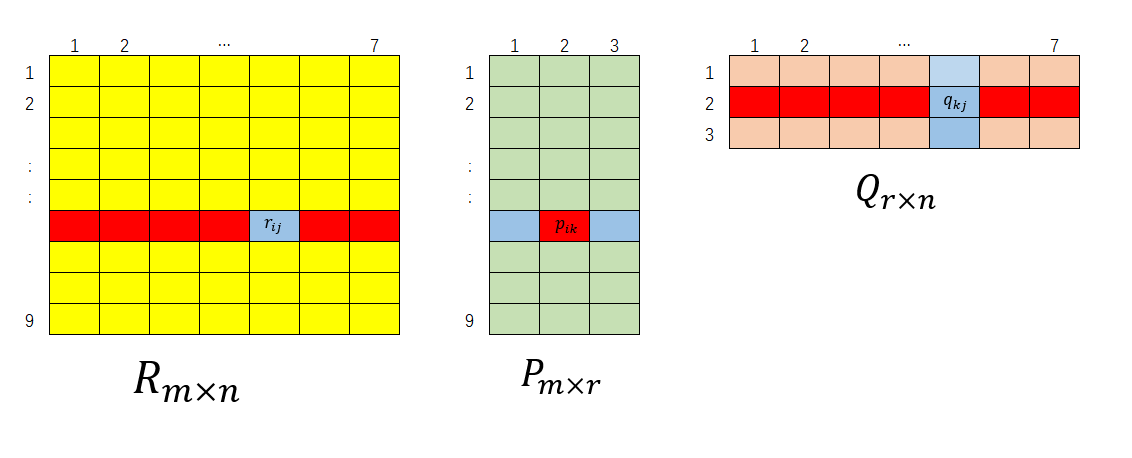
　　1  $ \sum _{\left(i,j \right) \in D} \left( r_{ij} - \sum_{k=1}^{r} p_{ik} q_{kj}\right)q_{kj} $ 中并不是所有项都有定义的，只取有定义位置。

　　2  对于给定的元素 $ p_{ik} $，i,k都是确定的，$ \sum _{\left(i,j \right) \in D} \left( r_{ij} - \sum_{k=1}^{r} p_{ik} q_{kj}\right)q_{kj} $所以可以看成$ \left ( \hat{R} -R \right )$ 和 Q 红色非空部分的内积, 进一步还能得到因子矩阵的梯度矩阵 $ \frac{\partial J}{\partial P}  = \left ( R-\hat{R} \right ) Q^T + \lambda P $

也可以直接用矩阵求导的方法来求解：

当然，做乘法时依然只是那些有记录的位置参与计算。