统计学习方法笔记 -- KNN

K近邻法（K-nearest neighbor，k-NN），这里只讨论基于knn的分类问题，1968年由Cover和Hart提出，属于判别模型
K近邻法不具有显式的学习过程，算法比较简单，每次分类都是根据训练集中k个最近邻，通过多数表决的方式进行预测。所以模型需要保留所有训练集数据，而象感知机这样的模型只需要保存训练后的参数即可，训练集不需要保留

K近邻算法

K近邻法三要素
和其他统计学习方法不同的，K近邻法的三要素是，k值的选择，距离度量和分类决策规则

距离度量
首先如何定义“近”？需要通过距离度量，比如最常见的欧氏距离
下面这个比较清楚，欧氏距离只是p=2的case，也称为L2距离

K值的选择
选取比较小的k值（较复杂的模型），近似误差（approximation error）会减小，而估计误差（estimation error）会增大，因为影响分类的都是比较近的样本，但一旦出现噪点，预测就会出错
选取比较大的k值（较简单的模型），相反，减小噪点的影响，但是较远或不相似的样本也会对结果有影响，极限情况下k=N，考虑所有样本，极简模型
k一般会选取比较小的值，通常采用交叉验证来选取最优的k值

分类决策规则
往往采用多数表决，但是也可以采用其他的策略

kd树

对于knn有个根本问题是，当训练集比较大时，线性的扫描效率是很低的，需要更为高效的方法来找到k近邻，这里介绍的kd数是二叉树，其实就是以二分的方式查找，将复杂度由n变小为logn。
那么关键问题就是，如何能够二分的索引训练点和给定任意一个点如何从kd树中找到最近邻？

构造kd树
基本思路，循环的以k维空间中的每一维对训练数据进行划分
划分标准，往往是使用训练集在该维上的中位数进行划分，具体看下下面的例子
使用中位数可以保证树是平衡的，但不一定效率最优

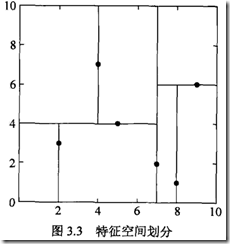
例子，
首先用x维划分，中位数为7，(7,2)放在节点上
(2,3) (4,7) (5,4)划分到左子树，而(8,1) (9,6)划分到右子树
然后用y维进行划分，
对于左边区域，y维的中位数为4，(4,7)放在节点上，(2,3) (5,4)分布划分到两个子树
对于右边区域，y维的中位数为6。。。
然后再用x维进行划分。。。

搜索kd树
对于搜索k邻近，就是k次搜索最邻近，所以直接看下最邻近的搜索算法
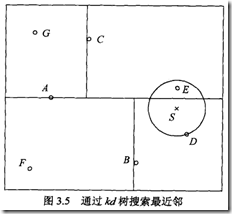
例子学习，
首先找到包含S的那个叶节点，这里是D，那么以SD为半径画个圆，有可能包含更近节点的区域一定会和这个圆相交，相交不一定有，但不相交一定没有
所以下面做的只是往根节点回溯，
首先B，B本身不是更近的节点，而B的另一个子节点F的区域和圆不相交
继续回溯到A，A不是，但A的另一个子节点C的区域是和圆相交的
所以需要checkA的C节点，C本身不是，G的区域不相交，但E的区域相交
并且E到S的距离更近，故E是最邻近节点