Awk使用方法简介

==================AWK===================
AWK简介：awk是一个强大的文本分析工具，相对于grep的查找，sed的编辑，awk在其对数据分析并生成报告时，显得尤为强大。简单来说awk就是把文件逐行的读入，                   以空格为默认分隔符将每行切片，切开的部分再进行各种分析处理；awk有3个不同版本: awk、nawk和gawk，未作特别说明，一般指gawk，gawk 是 AWK 的
                  GNU版本。

（1）域分隔符：awk在没有使用-F指定分割符时，默认以空格为分割符；
　　　　　　     域分割 $0代表文本内容全文显示；
　　　　　　　  $1 代表分割第一个域；
                          $2 代表分割第二个域；
　　　　　　　  ......
　　　　　　　 awk -F: 分割符为‘：’
　　　　　　　 eg： cat /etc/passwd | awk -F: '{print $1,$2,}'

（2） 打印报告头：
　　　　 eg: cat /etc/passwd | awk -F: 'BEGIN{print "This is system user"}{print $1}' | more

打印结尾：
　　　　eg: cat /etc/passwd | awk -F: 'BEGIN{print "This is system user"}{print $1}END{"=================="}' | more

　　　　　  cat /etc/passwd |awk -F: ‘BEGIN{print “===============”}{print $1}END{print “==========”}’  |more

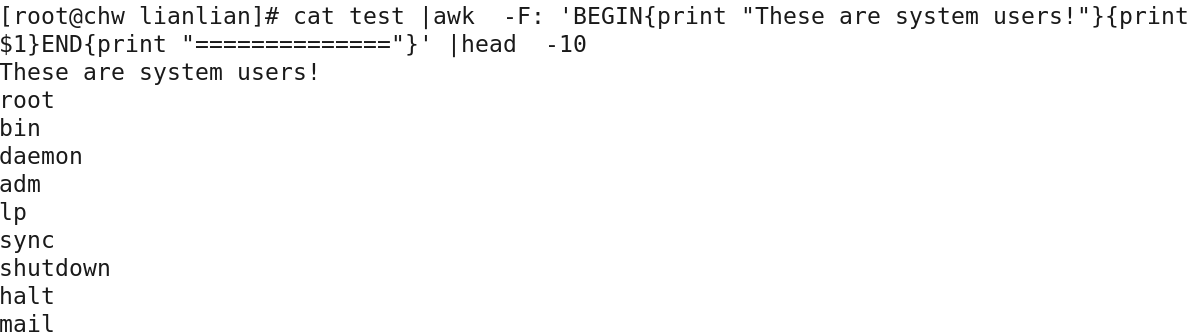
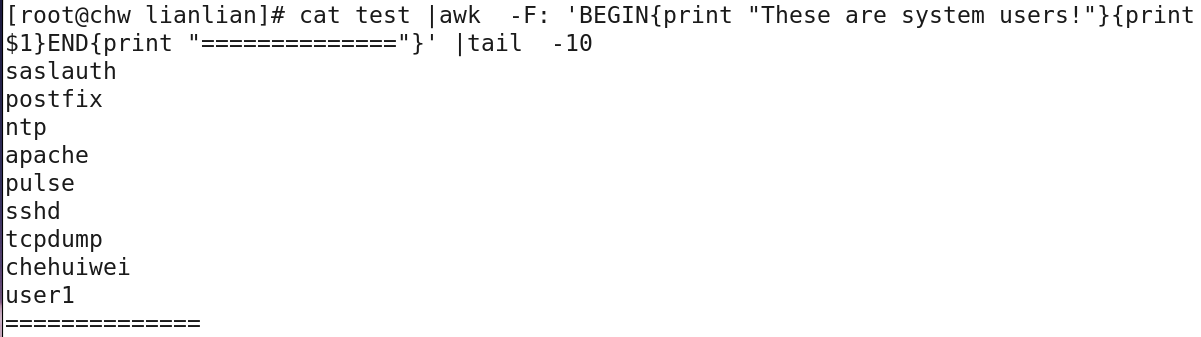
(3) awk 中的正则表达式：

　　　1>匹配 ~
　　　　　　eg: cat /etc/passwd |awk '{if($1~/root/) print $0}'
　　　　　　　   cat /etc/passwd |awk ‘$0~/root/’

                  

               2>精确匹配：
　　　　　　eg: cat /etc/passwd | awk -F: '$1=="root"{print $0}'   

                      

                  3> 不匹配：
　　　　　　　　eg: cat /etc/passwd |awk '{if($1!~/root/) print $0}'
　　　　　　　　　   cat /etc/passwd | awk '$0 !~ /root/'

                         

                    4>小于，小于或等于：
　　　　　　　　eg: cat /etc/passwd | awk -F: '{if($3<200) print $3}'
　　　　　　　　　   cat /etc/passwd | awk -F: '{if($3<=200) print $3}'           

                        

           

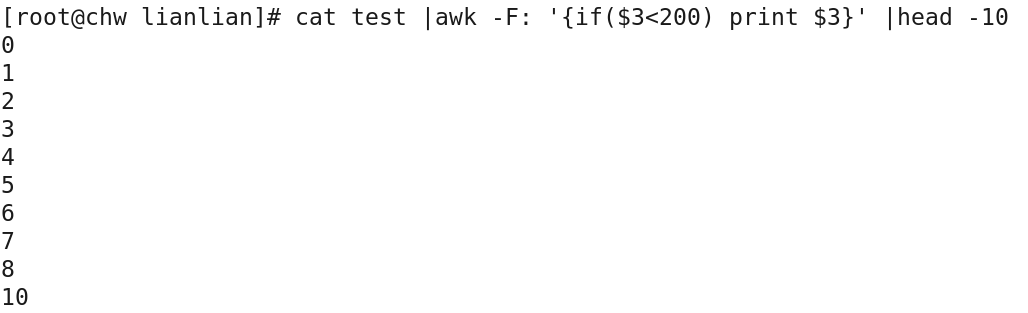
　　  5>大于，大于或等于：
　　　　　　eg: cat /etc/passwd | awk -F: '{if($3>500) print $3}'
　　　　　　　  cat /etc/passwd | awk -F: '{if($3>=500) print $3}'

                 

            6> 匹配多个关键字：
　　　　　　eg:
　　　　　　　　cat /etc/passwd | awk -F: '$1 ~ /(root|user)/ {print $0}'

                  

               7> 匹配行首：
　　　　　　　　eg: cat test |awk -F: ‘{if($1~/^root/) print $0}’
　　　　　　　　　   cat test |awk -F: ‘$1~/^root/ {print $0}’

                     

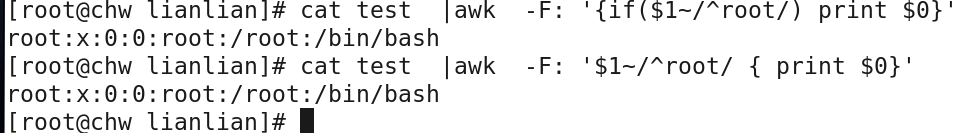
                     8> awk 使用 && ||
　　　　　　　　　　eg: cat /etc/passwd | awk -F: '{if($1=="root" && $5=="root") print $0}'
　　　　　　　　　　　   cat /etc/passwd | awk -F: '{if($1=="root" || $1=="sfsdfdsfds") print $0}' 

                    

(4) awk 中的NF与NR：
　　NF：浏览记录的域的个数（统计列的段数）
　　NR：统计列的行号
　　eg: cat test |awk -F: ‘{print NF}’ 输出一共有多少列
　　　  cat test |awk -F: ‘{print NF,NR}’ 输出一共有多少列及其行号
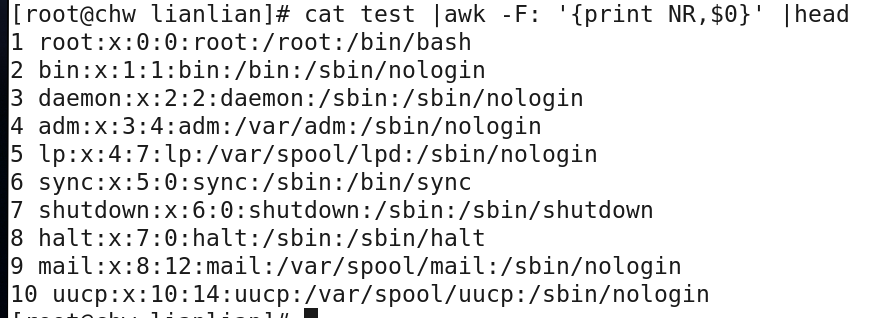
　　　  cat test |awk -F: ‘{print NR,$0}’ 输出全部内容，并在其前输出行号
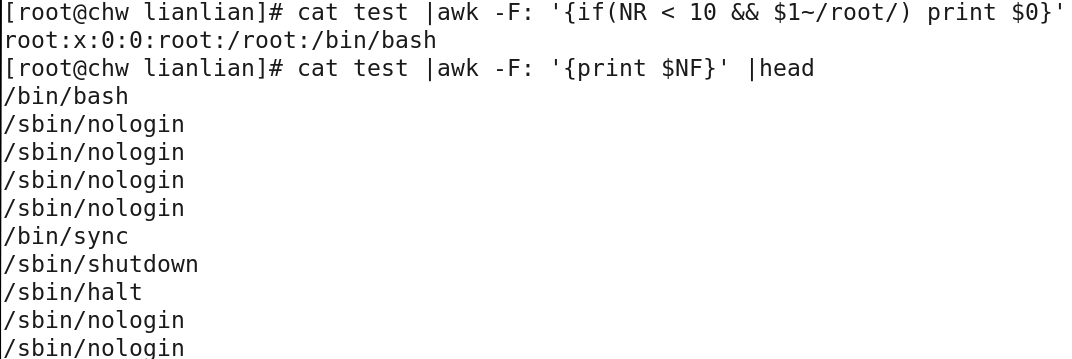
　　　  awk '{if(NR<10 && $1~/root/) print $1}' /etc/passwd 行号小于10的，使用$1匹配root关键字
　　　  cat /etc/passwd | awk -F: '{print $NF}' 打印每段的最后一段   

           

           

  （5）awk替换：
　　　　eg:cat /etc/passwd | awk 'gsub(/root/,"alvinzeng") ' 将文中所有的root替换成alvinzeng，并输出了所有匹配的行