LeetCode第十二题-将数字转化为罗马数字

Integer to Roman

问题简介：将输入的int类型数字转化为罗马数字

问题详解：罗马数字由七个不同的符号表示：I，V，X，L，C，D和M

符号-数值

I - 1

V - 5

X -10

L - 50

C - 100

D - 500

M - 1000

例如,2用罗马数字写成II,只有两个I加在一起,十二写为XII,解释为X + II, 二十七写成XXVII,即XX + V + II,

罗马数字通常从左到右从最大到最小,但是,四个数字不是IIII,相反,第四个写为IV,因为一个在五个之前,我们减去四个,同样的原则适用于九,即IX,有六个使用减法的实例：

我可以放在V（5）和X（10）之前做4和9,

X可以放在L（50）和C（100）之前,以产生40和90,

C可以放在D（500）和M（1000）之前，以产生400和900,

给定一个整数,将其转换为罗马数字。,输入保证在1到3999的范围内.

举例：

1:

输入: 3

输出: “III”

2:

输入: 4

输出: “IV”

3:

输入: 9

输出: “IX”

4:

输入: 58

输出: “LVIII”

解释: L = 50, V = 5, III = 3.

5:

输入: 1994

输出: “MCMXCIV”

解释: M = 1000, CM = 900, XC = 90 and IV = 4.

解法一：

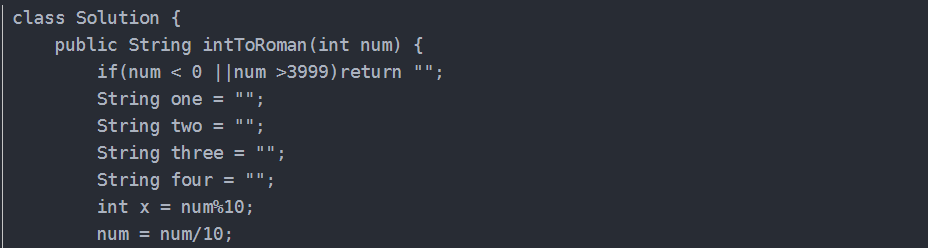
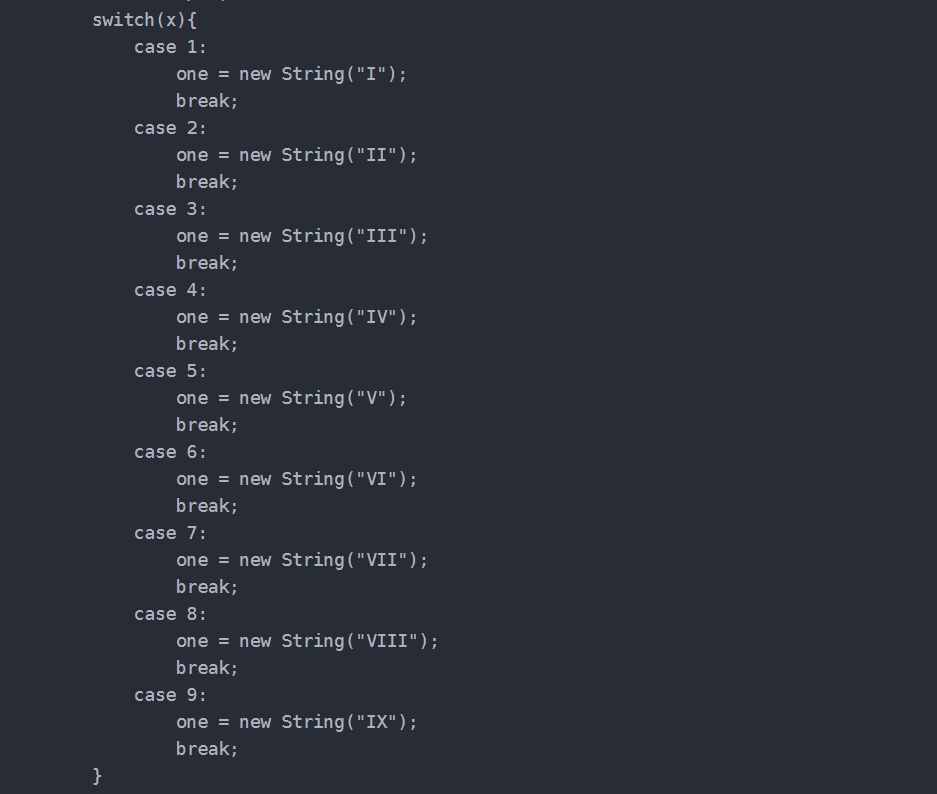
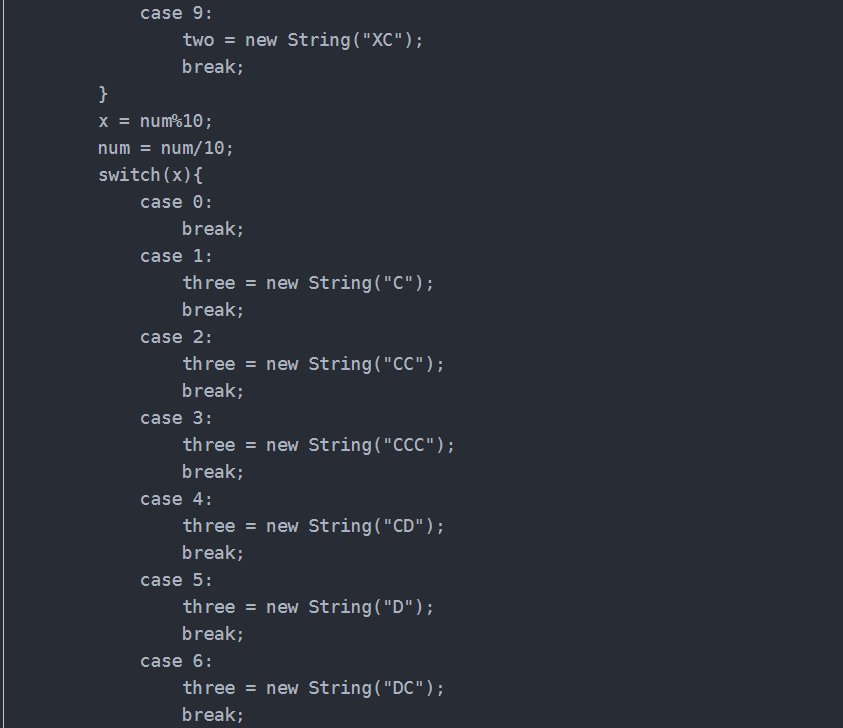
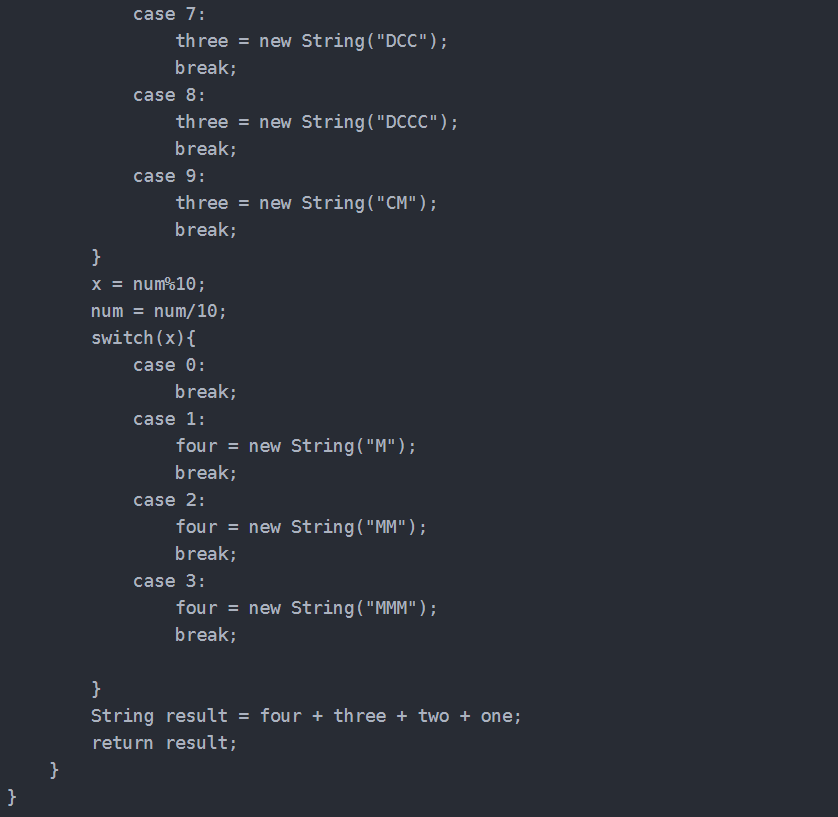
我这可能算穷举法。。。

因为输入1-3999的数字，也就是把每位的数字做处理

小白刷题之路,请多指教— — 要么大器晚成,要么石沉大海