Day6 Numerical simulation of optical wave propagation之通过随机介质（如大气湍流）的传播（二）

2.蒙特卡洛相位屏

大气折射率变化是一个随机的过程，通过大气的光程长度也同样是随机的。因此，湍流模型仅给出统计平均值，如折射率变量的结构函数和功率谱。

建立大气相位屏的问题就是产生随机过程独立表达式的问题，即相位屏的建立是通过把计算机产生的随机数变换为采样点网格上的两维相位值阵列来实现的，相位值阵列具有与湍流引起的相位变化相同的统计特性。

为了在有限的网格上生成相位屏，相位通常被写成各种基底函数的权重加和，常用于这一目的的基组为泽尔尼克多项式和傅里叶数列（FS），这两种基组各有优缺点。

（一）FT方法——最普遍的相位屏生成方法

湍流诱导光学相位为

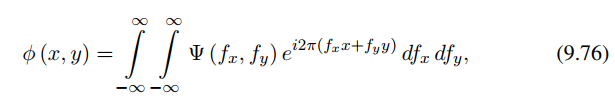
改写成傅里叶级数

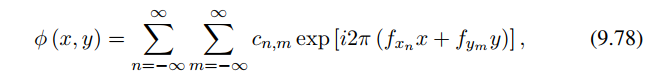
傅里叶系数C_n,m 服从具有零平均值和方差的环形复高斯统计，其中傅里叶系数C_n,m 的方差推导过程如下：

将9.78带入到9.77，可得如下结果

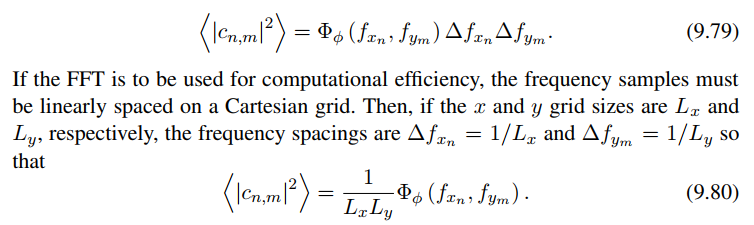
其中如下为改进的von-karman refractive-index PSD’s  ,单位为cycles/m

总结程序过程：首先利用MATLAB的randn函数，生成零平均值和单位方差的高斯随机数，然后乘以（9.79）给出的方差均根值便得到了傅里叶系数C_n,m的随机曲线。进而利用二维DIFT得到相位屏。详细代码见ft_sh_phase_screen子函数。

（二）分谐波强化的FT方法——

上述FT方法中采用的二维DIFT不能生成准确的相位屏，最大偏差发生在大空间间隔处，即低空间频率处。——由（9.51）生成的相位PSD在较低空间频率具有很高的功率。实际上很多文献表明经常不能对足够低的空间频率进行采样来准确表征低阶模式，如倾斜。

基本原理：首先采用上述二维DIFT法生成相位屏，然后在相位屏中间的低频处这一小范围内采用分谐波法生成低频相位屏，即利用多个分谐波的和得到相位屏中间的低频处的相位，相应低频处相位的公式如下。详细代码见ft_phase_screen子函数。

注：分谐波是指频率等于一个周期性振荡基频的整分数的正弦分量。例如,频率等于基频二分之一的波称为二次分谐波，三分之一的波称为三次分谐波等。